程式 = 演算法 + 數據結構

對應到電腦的組成原理(硬體層面)

• 演算法 --- 各種電腦指令
• 數據結構 --- 二進位數據

電腦用0/1組成的二進位，來表示所有信息

• 程式指令用到的機器碼，是使用二進位表示的
• 存儲在記憶體裡面的字元串、整數、浮點數也都是用二進位表示的

萬物在電腦里都是0和1，搞清楚各種數據在二進位層面是怎麼表示的，是我們的必修課。

在實際應用中最常遇到的問題，也就是文本字元串是怎麼表示成二進位的，特別是我們會遇到的亂碼究竟是怎麼回事兒

在開發的時候，所說的Unicode和UTF-8之間有什麼關係。

理解了這些，相信以後遇到任何亂碼問題，你都能手到擒來了。

1 理解二進位的“逢二進一”

二進位和我們平時用的十進位，並沒有本質區別，只是平時是“逢十進一”，這裡變成了“逢二進一”

每一位，相比於十進位下的0～9這十個數字，我們只能用0和1這兩個數字。

任何一個十進位的整數，都能通過二進位表示出來

把一個二進位數，對應到十進位，非常簡單，就是把從右到左的第N位，乘上一個2的N次方，然後加起來，就變成了一個十進位數

當然，既然二進位是一個面向程式員的“語言”，這個從右到左的位置，自然是從0開始的。

比如_0011_這個二進位數，對應的十進位表示，就是

\(0×2^3+0×2^2+1×2^1+1×2^0\)
\(=3\)

代表十進位的3

對應地，如果我們想要把一個十進位的數，轉化成二進位，使用短除法就可以了

也就是，把十進位數除以2的餘數，作為最右邊的一位。然後用商繼續除以2，把對應的餘數緊靠著剛纔餘數的右側，這樣遞歸迭代，直到商為0就可以了。

• 比如，我們想把13這個十進位數，用短除法轉化成二進位，需要經歷以下幾個步驟：
  
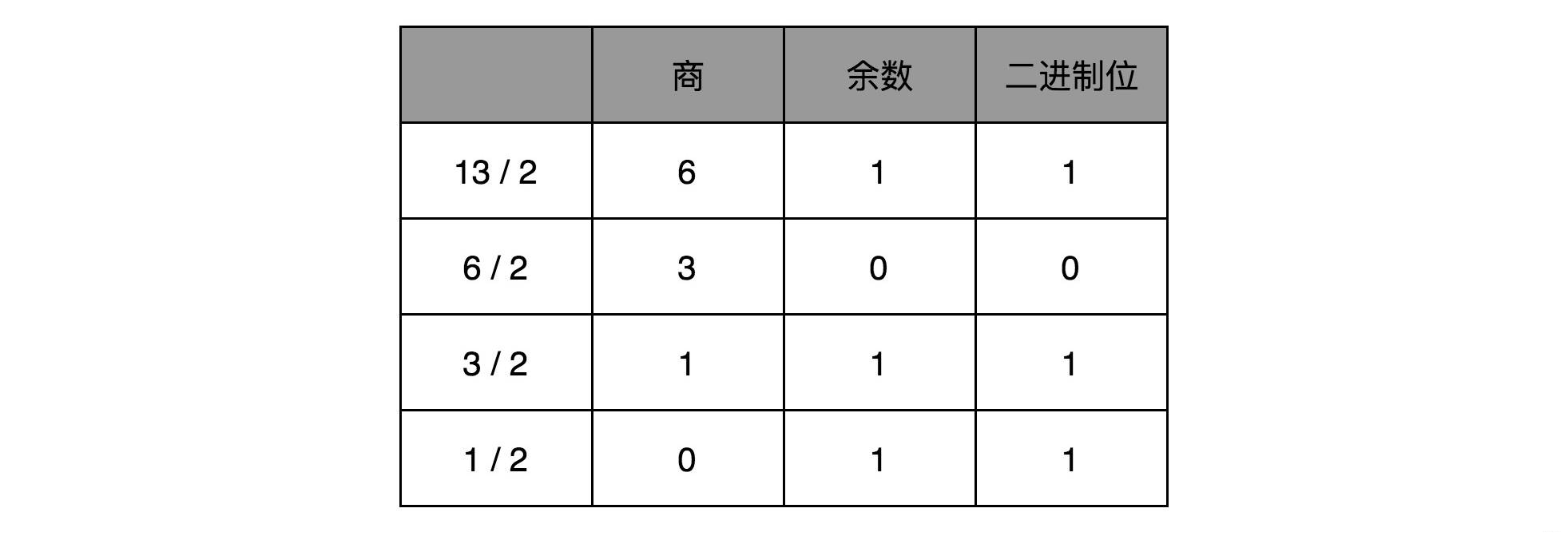
  因此，對應的二進位數，就是1101

剛纔我們舉的例子都是正數，對於負數來說，情況也是一樣的嗎？

我們可以把一個數最左側的一位，當成是對應的正負號，比如0為正數，1為負數，這樣來進行標記。

這樣，一個4位的二進位數， 0011就表示為+3。而1011最左側的第一位是1，所以它就表示-3。這個其實就是整數的原碼表示法

原碼表示法有一個很直觀的缺點就是，0可以用兩個不同的編碼來表示，1000代表0， 0000也代表0。習慣萬事一一對應的程式員看到這種情況，必然會被“逼死”。

於是，我們就有了另一種表示方法。我們仍然通過最左側第一位的0和1，來判斷這個數的正負。但是，我們不再把這一位當成單獨的符號位，在剩下幾位計算出的十進位前加上正負號，而是在計算整個二進位值的時候，在左側最高位前面加個負號。

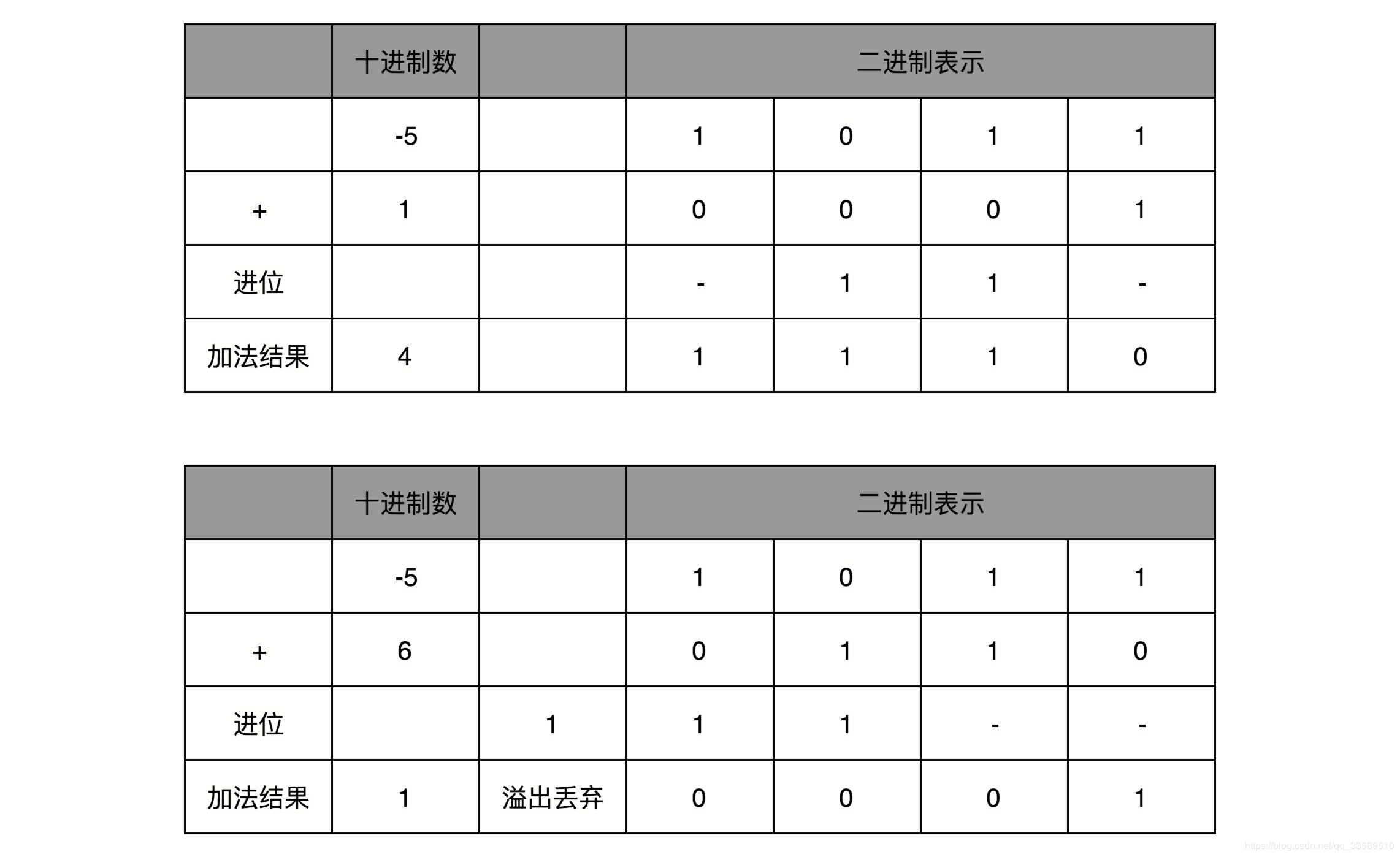
比如，一個4位的二進位補碼數值1011，轉換成十進位，就是

\(-1×2^3+0×2^2+1×2^1+1×2^0\)
\(=-5\)

如果最高位是1，這個數必然是負數；最高位是0，必然是正數。並且，只有0000表示0，1000在這樣的情況下表示-8。一個4位的二進位數，可以表示從-8到7這16個整數，不會白白浪費一位。

當然更重要的一點是，用補碼來表示負數，使得我們的整數相加變得很容易，不需要做任何特殊處理，只是把它當成普通的二進位相加，就能得到正確的結果。

我們簡單一點，拿一個4位的整數來算一下，比如 -5 + 4 = -1，-5 + 6 = 1

我們各自把它們轉換成二進位來看一看。如果它們和無符號的二進位整數的加法用的是同樣的計算方式，這也就意味著它們是同樣的電路。

2 字元串的表示，從編碼到數字

不僅數值可以用二進位表示，字元乃至更多的信息都能用二進位表示

最典型的例子就是字元串（Character String）

最早電腦只需要使用英文字元，加上數字和一些特殊符號，然後用8位的二進位，就能表示我們日常需要的所有字元了，這個就是我們常常說的ASCII碼（American Standard Code for Information Interchange，美國信息交換標準代碼）

ASCII碼就好比一個字典，用8位二進位中的128個不同的數，映射到128個不同的字元里

比如，小寫字母a在ASCII裡面，就是第97個，也就是二進位的0110 0001，對應的十六進位表示就是 61。而大寫字母 A，就是第65個，也就是二進位的0100 0001，對應的十六進位表示就是41。

在ASCII碼裡面，數字9不再像整數表示法里一樣，用0000 1001來表示，而是用0011 1001 來表示。字元串15也不是用0000 1111 這8位來表示，而是變成兩個字元1和5連續放在一起，也就是 0011 0001 和 0011 0101，需要用兩個8位來表示。

我們可以看到，最大的32位整數，就是2147483647。如果用整數表示法，只需要32位就能表示了。但是如果用字元串來表示，一共有10個字元，每個字元用8位的話，需要整整80位。比起整數表示法，要多占很多空間。

這也是為什麼，很多時候我們在存儲數據的時候，要採用二進位序列化這樣的方式，而不是簡單地把數據通過CSV或者JSON，這樣的文本格式存儲來進行序列化。不管是整數也好，浮點數也好，採用二進位序列化會比存儲文本省下不少空間。

ASCII碼只表示了128個字元，一開始倒也堪用，畢竟電腦是在美國發明的

然而隨著越來越多的不同國家的人都用上了電腦，想要表示譬如中文這樣的文字，128個字元顯然是不太夠用的。於是，電腦工程師們開始各顯神通，給自己國家的語言創建了對應的字元集（Charset）和字元編碼（Character Encoding）

字元集

表示的可以是字元的一個集合

比如“中文”就是一個字元集，不過這樣描述一個字元集並不准確

想要更精確一點，我們可以說，“第一版《新華字典》裡面出現的所有漢字”，這是一個字元集。這樣，我們才能明確知道，一個字元在不在這個集合裡面

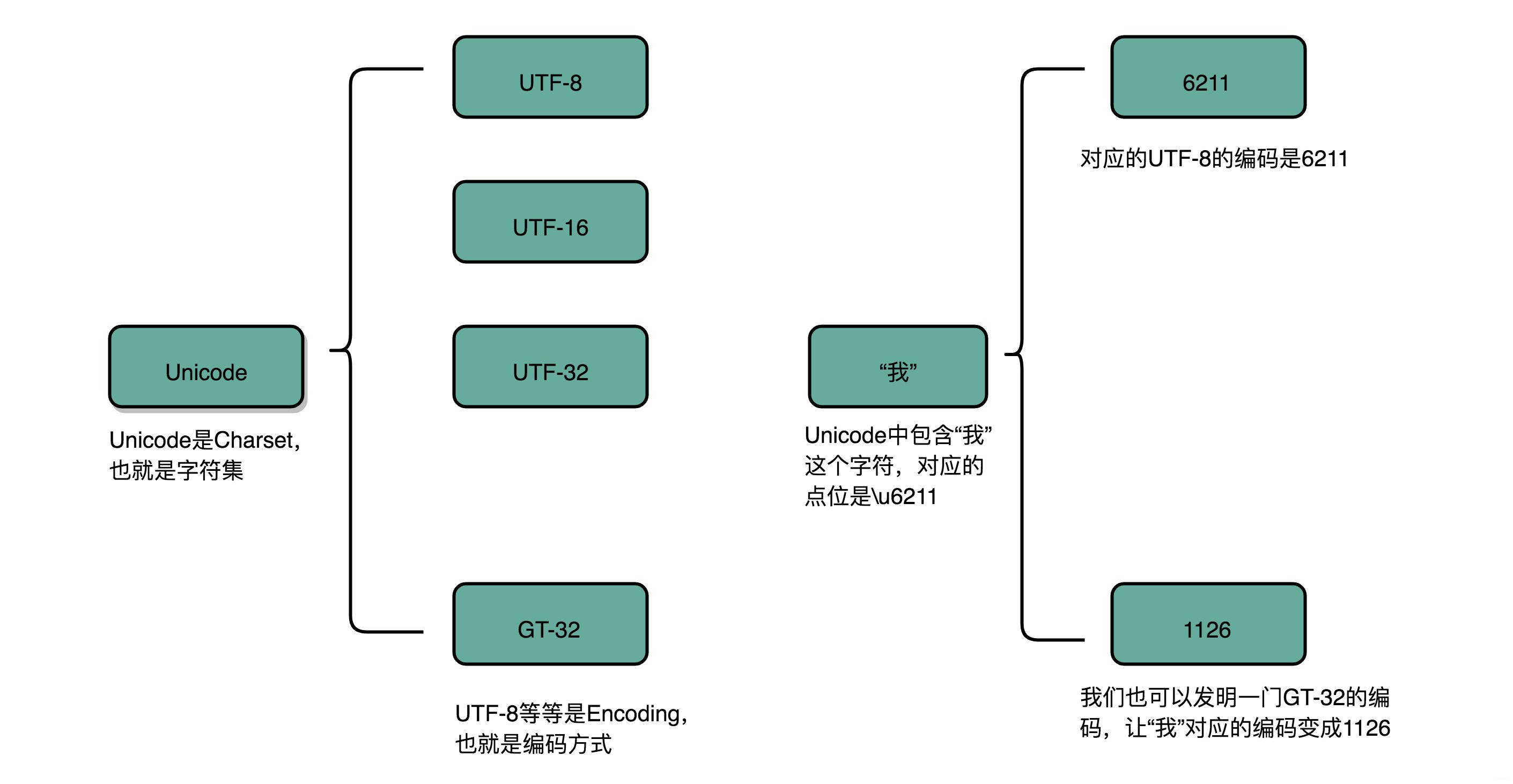
比如，我們日常說的Unicode，其實就是一個字元集，包含了150種語言的14萬個不同的字元。

字元編碼

則是對於字元集里的這些字元，怎麼一一用二進位表示出來的一個字典

我們上面說的Unicode，就可以用UTF-8、UTF-16，乃至UTF-32來進行編碼，存儲成二進位。所以，有了Unicode，其實我們可以用不止UTF-8一種編碼形式，我們也可以自己發明一套 GT-32 編碼，比如就叫作Geek Time 32好了。只要別人知道這套編碼規則，就可以正常傳輸、顯示這段代碼。

同樣的文本，採用不同的編碼存儲下來。如果另外一個程式，用一種不同的編碼方式來進行解碼和展示，就會出現亂碼。這就好像兩個軍隊用密語通信，如果用錯了密碼本，那看到的消息就會不知所云。在中文世界里，最典型的就是“手持兩把錕斤拷，口中疾呼燙燙燙”的典故。

沒有經驗的同學，在看到程式輸出“燙燙燙”的時候，以為是程式讓CPU過熱發出報警，於是嘗試給CPU降頻來解決問題。

既然今天要徹底搞清楚編碼知識，我們就來弄清楚“錕斤拷”和“燙燙燙”的來龍去脈。

“錕斤拷”的來源

如果我們想要用Unicode編碼記錄一些文本，特別是一些遺留的老字元集內的文本，但是這些字元在Unicode中可能並不存在。於是，Unicode會統一把這些字元記錄為U+FFFD這個編碼

如果用UTF-8的格式存儲下來，就是\xef\xbf\xbd。如果連續兩個這樣的字元放在一起，\xef\xbf\xbd\xef\xbf\xbd，這個時候，如果程式把這個字元，用GB2312的方式進行decode，就會變成“錕斤拷”。這就好比我們用GB2312這本密碼本，去解密別人用UTF-8加密的信息，自然沒辦法讀出有用的信息。

而“燙燙燙”，則是因為如果你用了Visual Studio的調試器，預設使用MBCS字元集

“燙”在裡面是由0xCCCC來表示的，而0xCC又恰好是未初始化的記憶體的賦值。於是，在讀到沒有賦值的記憶體地址或者變數的時候，電腦就開始大叫“燙燙燙”了。

3 總結延伸

到這裡，相信你發現，我們可以用二進位編碼的方式，表示任意的信息。只要建立起字元集和字元編碼，並且得到大家的認同，我們就可以在電腦裡面表示這樣的信息了。所以說，如果你有心，要發明一門自己的克林貢語並不是什麼難事。

不過，光是明白怎麼把數值和字元在邏輯層面用二進位表示是不夠的。我們在電腦組成裡面，關心的不只是數值和字元的邏輯表示，更要弄明白，在硬體層面，這些數值和我們一直提的晶體管和電路有什麼關係。下一講，我就會為你揭開神秘的面紗。我會從時鐘和D觸發器講起，最終讓你明白，電腦里的加法，是如何通過電路來實現的。

4 推薦閱讀

• 《編碼：隱匿在電腦軟硬體背後的語言》
  
  從電報機到電腦，這本書講述了很多計算設備的歷史故事，當然，也包含了二進位及其背後對應的電路原理。

參考

• 深入淺出電腦組成原理