相似基因

相似基因

題目

【題目描述】

大家都知道，基因可以看作一個鹼基對序列。它包含了4種核苷酸，簡記作A,C,G,T。生物學家正致力於尋找人類基因的功能，以利用於診斷疾病和發明藥物。

在一個人類基因工作組的任務中，生物學家研究的是：兩個基因的相似程度。因為這個研究對疾病的治療有著非同尋常的作用。

兩個基因的相似度的計算方法如下：

對於兩個已知基因，例如AGTGATG和GTTAG，將它們的鹼基互相對應。當然，中間可以加入一些空鹼基-，例如：

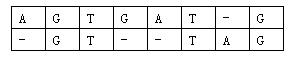
這樣,兩個基因之間的相似度就可以用鹼基之間相似度的總和來描述，鹼基之間的相似度如下表所示：

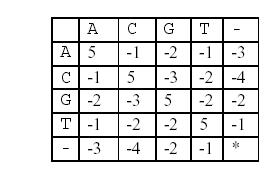
那麼相似度就是：(-3)+5+5+(-2)+(-3)+5+(-3)+5=9。因為兩個基因的對應方法不唯一，例如又有：

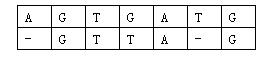
相似度為：(-3)+5+5+(-2)+5+(-1)+5=14。規定兩個基因的相似度為所有對應方法中，相似度最大的那個。

【輸入格式】

共兩行。每行首先是一個整數，表示基因的長度；隔一個空格後是一個基因序列，序列中只含A,C,G,T四個字母。

【輸出格式】

僅一行，即輸入基因的相似度。

【數據規模】

1≤序列的長度≤100。

解析

很明顯的一道動態規劃題。因為有兩組基因，所以不難推出狀態：f[i][j]，表示前i個基因A與前j個基因B的相似度。

故得出狀態轉移方程：f[i][j]=f[i-1][j-1]+x(x表示基因i與基因j的相似度)

由於可以加入空鹼基-，所以還有另外兩種轉移方式：

f[i][j]=f[i][j-1]+x(即在基因A中加入空鹼基);

f[i][j]=f[i-1][j]+x(即在基因B中加入空鹼基)。

邊界為：f[0][0]=0與f[i][0]=f[i-1][0]+x與f[0][i]=f[0][i-1]+x；即無基因與各個基因與空鹼基的相似度。

相似度的計算可以採用二維數組存儲或函數計算。

Code

#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
#include <cmath>
using namespace std;
int l1,l2,f[101][101];//f[i][j]表示前i個基因A與前j個基因B的相似度 
//f[i][j]=f[i-1][j-1]+x或f[i][j-1]+x或f[i-1][j]+x
char s1[101],s2[101],s='-';
int xs(char a,char b)//相似度 
{
    if(a==b) return 5;
    if(a=='A')
    {
        if(b=='C') return -1;
        if(b=='G') return -2;
        if(b=='T') return -1;
        if(b=='-') return -3;
    }
    if(a=='C')
    {
        if(b=='G') return -3;
        if(b=='T') return -2;
        if(b=='-') return -4;
    }
    if(a=='G')
    {
        if(b=='T') return -2;
        if(b=='-') return -2;
    }
    if(a=='T'&&b=='-') return -1;
    return xs(b,a);
}
int main()
{
    memset(f,0xcf,sizeof(f));
    f[0][0]=0;
    cin>>l1;
    for(int i=1;i<=l1;i++)
    {
        cin>>s1[i];
        f[i][0]=f[i-1][0]+xs(s1[i],s);
    }
    cin>>l2;
    for(int i=1;i<=l2;i++)
    {
        cin>>s2[i];
        f[0][i]=f[0][i-1]+xs(s2[i],s);
    }
    for(int i=1;i<=l1;i++)
        for(int j=1;j<=l2;j++)
        {
            f[i][j]=max(f[i][j],f[i-1][j-1]+xs(s1[i],s2[j]));
            f[i][j]=max(f[i][j],f[i][j-1]+xs(s2[j],s));
            f[i][j]=max(f[i][j],f[i-1][j]+xs(s1[i],s));
        }
    cout<<f[l1][l2];
    return 0;
}