一、二叉樹回憶 上一篇我們對數據結構中常用的樹做了介紹,本篇博客主要以二叉樹為例,講解一下樹的數據結構和代碼實現。回顧二叉樹:二叉樹是每個節點最多有兩個子樹的樹結構。通常子樹被稱作“左子樹”(left subtree)和“右子樹”(right subtree) 二、二叉樹比鏈表好在哪裡? 看看如下的 ...
一、二叉樹回憶
上一篇我們對數據結構中常用的樹做了介紹,本篇博客主要以二叉樹為例,講解一下樹的數據結構和代碼實現。回顧二叉樹:二叉樹是每個節點最多有兩個子樹的樹結構。通常子樹被稱作“左子樹”(left subtree)和“右子樹”(right subtree)
二、二叉樹比鏈表好在哪裡?
看看如下的數據:使用鏈表形式存放

我們要向查找數據6,需要從頭開始查找,找到最後一個,查找比較麻煩。再來看看使用二叉樹的形式存儲
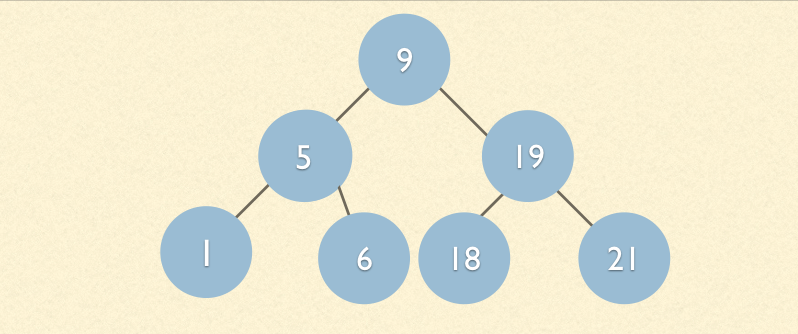
顯然,我們很清楚自己要查找的目標大致會在那裡出現;
例如查找的目標是6,那麼我知道6小於9所以根本不會去看右邊的數據;
我們繼續看6大於5所以找到啦目標;
換句話說我們只對比了兩次找到啦目標;
而對於鏈表,我們發現6排在了鏈表的尾部;到此為止我們知道這樣的二叉樹的確是高效的;
三、二叉樹的節點定義(C語言版)
typedef struct N { int data; struct N *left_node; struct N *right_node; }Node;
四、定義一個二叉樹(C語言版)
typedef struct tree { struct node *root; }Tree;
我們的樹定義得更加簡單,註意我們是先定義節點,再定義樹;
因為樹的定義需要用到節點結構體;
接下來我們需要初始化我們的樹
五、初始化樹(C語言版)
Tree * init_tree() { Tree *tree = (Tree *)malloc(sizeof(Tree)); if (tree) { tree->root = NULL; } return tree; }
六、創建節點(C語言版)
Node *make_node(int data) { Node *node = (Node *)malloc(sizeof(Node)); node->left_node = NULL; node->right_node = NULL; node->data = data; return node; }
七、插入節點(C語言版)
// 插入節點 Node* insert_node(Tree *tree,int data) { // 判斷根節點是否存在 if (tree->root == NULL) { // 不存在就創建 tree->root = make_node(data); } else { Node *current = tree->root; // 一直迴圈知道找到準確的插入數據的位置 while (1) { // 我們的二叉樹不允許重覆數字插入,相等直接退出 if (current->data == data) { return tree->root; } // 如果要插入的數據比根節點大,就放在右邊的子樹中 else if(current->data<data) { if (current->right_node == NULL) { // 創建右節點 current->right_node = make_node(data); break; } current = current->right_node; } else { // 如果要插入的數據比根節點小,就放在左邊的子樹中 if (current->left_node == NULL) { // 創建左節點 current->left_node = make_node(data); break; } current = current->left_node; } } } return tree->root; }
八、樹的遍歷(C語言版)
void print_inorder(Node *root) { if (root) { print_inorder(root->left_node); printf("data:%d\n",root->data); print_inorder(root->right_node); } }
九、樹的刪除(C語言版)
樹的刪除比較麻煩,整體分為二種情況:
一、要刪除的節點左右都有子節點
二、要刪除的節點只有一個或者0個節點(即有左節點或者右節點或者一個都沒有)
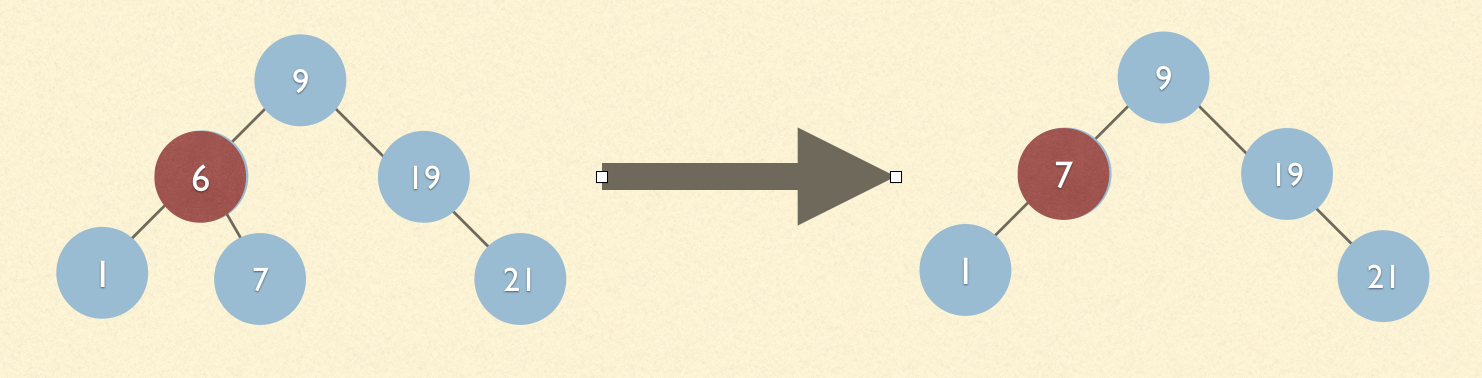
其中第一種情況又分幾種小情況。例如:我們要刪除節點6
1.1 我們現在要刪除的是節點6,這時候6節點下麵的右節點只有一個7,並且7下麵沒有節點,有一個也一樣的,只需要將其右邊的節點7替代他的位置即可。
1.2 我們現在要刪除的是節點6,現在7下麵5和8兩個節點,如果還是按照上面的思路刪除的話,刪除之後7下麵就有1,5,8三個節點,明顯不對
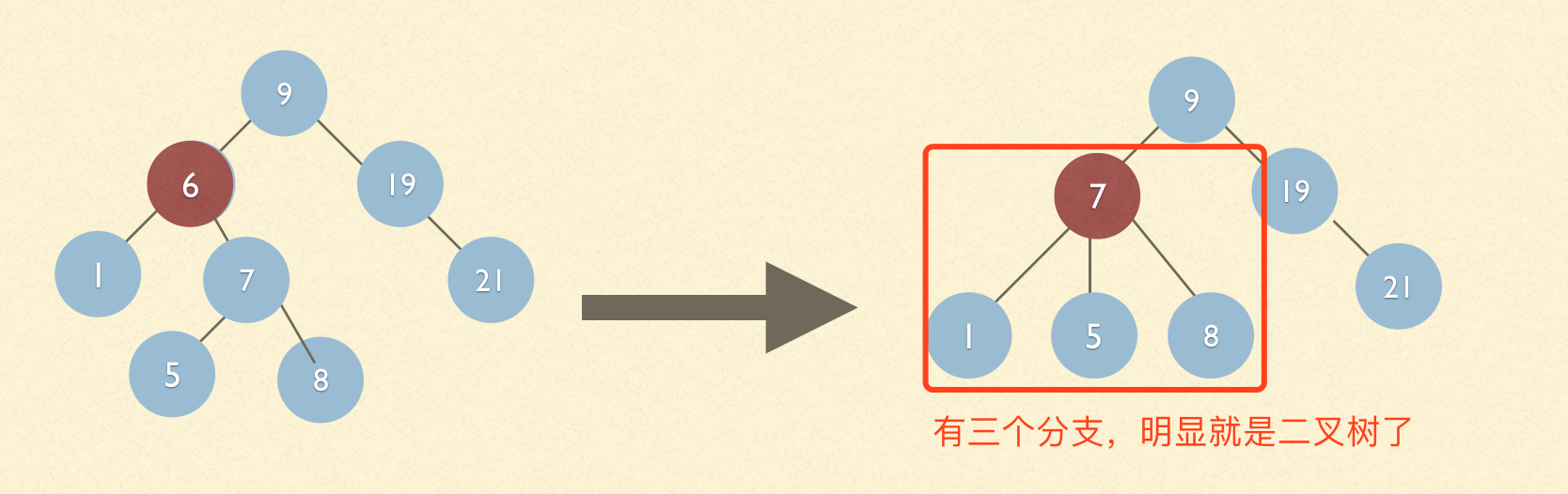
正確的做法應該是找到要刪除的節點6的右節點7,這時候在找到7的做節點5,去繼承刪除節點6的位置

1.3、以要刪除節點6的右節點7為樹的左邊分支的最小子節點是左節點的情況(很繞口)

1.4、以要刪除節點6的右節點7為樹的左邊分支的最小子節點是右節點的情況(很繞口)
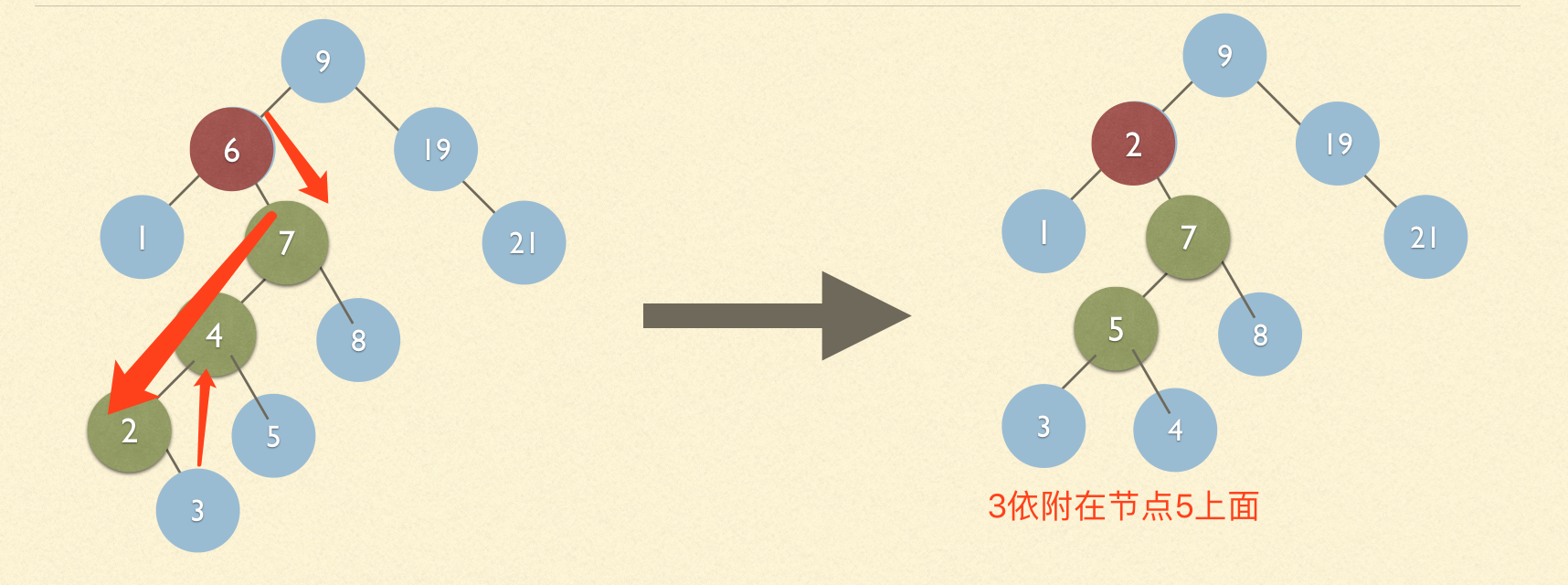
樹刪除代碼的實現
int remove_node(Tree *tree,int data) { if (tree->root != NULL) { Node *p = NULL; Node *s ; Node *current = tree->root; while (1) { // 根節點都沒有直接返回 if (current == NULL) { return 0; } // 要刪除的節點就是跟節點 else if(current->data == data) { break; } // 要刪除的節點在根節點的右邊 else if(current->data<data) { p = current; current = current->right_node; } // 要刪除的節點在根節點的左邊 else { p=current; current = current->left_node; } } /**********************上面的代碼片段是找到要刪除的節點**************************/ if (current->left_node != NULL && current->right_node != NULL) { p = current; // 找到要刪除節點的右節點 s = current->right_node; while (s->left_node != NULL) { // p = s當current要深入到下一個分叉時,給自己留一個後路;所以保存了自己的前一個備份; p = s; // 沿著左邊一直找到最小的節點 s = s->left_node; } current->data = s->data; // 最小值在分支的右邊 if ( p->right_node == s) { p->right_node = s->right_node; } free(s); } /***************上面的代碼片段是根據要刪除節點左右都有子節點的情況**************/ else { // 左子節點為空,只有右子節點 if (current->left_node == NULL) { // 而且要刪除的節點是跟節點 if (p==NULL) { // 直接將跟節點的右節點設置為跟節點 tree->root = current->right_node; } else { if (p->right_node == current) { p->right_node = current->right_node; } else { p->left_node = current->right_node; } } } // 右子節點為空,只有左子節點 else { // 而且要刪除的節點是跟節點 if (p == NULL) { tree->root = current->left_node; } else { if (p->right_node == current) { p->right_node = current->left_node; } else { p->left_node = current->left_node; } } } } /***************上面的代碼片段是根據要刪除節點左右只有一個或者沒有子節點的情況**********/ } return 1; }
十、樹的查找(C語言版)
int find_node(Node *root,int data) { if (root == NULL) { return 0; } else if(root->data == data) { return 1; } else { if (root->data <data) { return find_node(root->right_node, data); } else { return find_node(root->left_node, data); } } }
十一、樹的前序遍歷(C語言版)
void preOrder(Node *root) { if (root != NULL) { printf("%d ",root->data); preOrder(root->left_node); preOrder(root->right_node); } }
十二、樹的中序遍歷(C語言版)
void inOrder(Node *root) { if (root != NULL) { inOrder(root->left_node); printf("%d ",root->data); inOrder(root->right_node); } }
十三、樹的後序遍歷(C語言版)
void postOreder(Node *root) { if (root != NULL) { postOreder(root->left_node); postOreder(root->right_node); printf("%d ",root->data); } }
十四、樹的廣度遍歷(C語言版)
void level_order(Tree *tree) { Node *node = tree->root; Node *queue[10]; int current = 0; int after_current = 0; if (node == NULL) { return; } queue[current++] = node; while (current!=after_current) { node = queue[after_current++]; printf("%d ",node->data); if (node->left_node != NULL) { queue[current++] = node->left_node; } if (node->right_node != NULL) { queue[current++] = node->right_node; } } }
十五、樹的python代碼實現
由於C語言版寫的很詳細了,python就簡單的實現排序,思路完全一樣。
# coding:utf-8 class Node(object): """""" def __init__(self, item): self.elem = item self.lchild = None self.rchild = None class Tree(object): """二叉樹""" def __init__(self): self.root = None def add(self, item): node = Node(item) if self.root is None: self.root = node return queue = [self.root] while queue: cur_node = queue.pop(0) if cur_node.lchild is None: cur_node.lchild = node return else: queue.append(cur_node.lchild) if cur_node.rchild is None: cur_node.rchild = node return else: queue.append(cur_node.rchild) def breadth_travel(self): """廣度遍歷""" if self.root is None: return queue = [self.root] while queue: cur_node = queue.pop(0) print(cur_node.elem, end=" ") if cur_node.lchild is not None: queue.append(cur_node.lchild) if cur_node.rchild is not None: queue.append(cur_node.rchild) def preorder(self, node): """先序遍歷""" if node is None: return print(node.elem, end=" ") self.preorder(node.lchild) self.preorder(node.rchild) def inorder(self, node): """中序遍歷""" if node is None: return self.inorder(node.lchild) print(node.elem, end=" ") self.inorder(node.rchild) def postorder(self, node): """後序遍歷""" if node is None: return self.postorder(node.lchild) self.postorder(node.rchild) print(node.elem, end=" ") if __name__ == "__main__": tree = Tree() tree.add(5) tree.add(2) tree.add(3) tree.add(7) tree.add(4) tree.add(8) tree.add(6) tree.preorder(tree.root) print(" ") tree.inorder(tree.root) print(" ") tree.postorder(tree.root) print(" ") tree.breadth_travel()
運行結果為:
5 2 7 4 3 8 6 7 2 4 5 8 3 6 7 4 2 8 6 3 5 5 2 3 7 4 8 6
寫到此處以吐血,你看到次數也吐血了吧。



