c++性能測試工具：計算時間複雜度

有時候除了測量演算法的具體性能指數，我們也會希望測試出演算法的時間複雜度，以便我們對待測試的演算法的性能有一個更加直觀的瞭解。

測量時間複雜度

google benchmark已經為我們提供了類似的功能，而且使用相當簡單。

具體的解釋在後面，我們先來看幾個例子，我們人為製造幾個時間複雜度分別為O(n), O(logn), O(n^n)的測試用例：

// 這裡都是為了演示而寫成的代碼，沒有什麼實際意義
static void bench_N(benchmark::State& state)
{
    int n = 0;
    for ([[maybe_unused]] auto _ : state) {
        for (int i = 0; i < state.range(0); ++i) {
            benchmark::DoNotOptimize(n += 2); // 這個函數防止編譯器將表達式優化，會略微降低一些性能
        }
    }
    state.SetComplexityN(state.range(0));
}
BENCHMARK(bench_N)->RangeMultiplier(10)->Range(10, 1000000)->Complexity();

static void bench_LogN(benchmark::State& state)
{
    int n = 0;
    for ([[maybe_unused]] auto _ : state) {
        for (int i = 1; i < state.range(0); i *= 2) {
            benchmark::DoNotOptimize(n += 2);
        }
    }
    state.SetComplexityN(state.range(0));
}
BENCHMARK(bench_LogN)->RangeMultiplier(10)->Range(10, 1000000)->Complexity();

static void bench_Square(benchmark::State& state)
{
    int n = 0;
    auto len = state.range(0);
    for ([[maybe_unused]] auto _ : state) {
        for (int64_t i = 1; i < len*len; ++i) {
            benchmark::DoNotOptimize(n += 2);
        }
    }
    state.SetComplexityN(len);
}
BENCHMARK(bench_Square)->RangeMultiplier(10)->Range(10, 100000)->Complexity();

如何傳遞參數和生成批量測試我們在上一篇已經介紹過了，這裡不再重覆。

需要關註的是新出現的state.SetComplexityN和Complexity。

首先是state.SetComplexityN，參數是一個64位整數，用來表示演算法總體需要處理的數據總量。benchmark會根據這個數值，再加上運行耗時以及state的迭代次數計算出一個用於後面預估平均時間複雜度的值。

Complexity會根據同一組的多個測試用例計算出一個較接近的平均時間複雜度和一個均方根值，需要和state.SetComplexityN配合使用。

Complexity還有一個參數，可以接受一個函數或是benchmark::BigO枚舉，它的作用是提示benchmark該測試用例的時間複雜度，預設值為benchmark::oAuto，測試中會自動幫我們計算出時間複雜度。對於較為複雜的演算法，而我們又有預期的時間按複雜度，這時我們就可以將其傳給這個方法，比如對於第二個測試用例，我們還可以這樣寫：

static void bench_LogN(benchmark::State& state)
{
    // 中間部分與前面一樣，略過
}
BENCHMARK(bench_LogN)->RangeMultiplier(10)->Range(10, 1000000)->Complexity(benchmark::oLogN);

在選擇正確的提示後對測試結果幾乎沒有影響，除了偏差值可以降得更低，使結果更準確。

Complexity在計算時間複雜度時會保留複雜度的繫數，因此，如果我們發現給出的提示的時間複雜度前的繫數過大的話，就意味著我們的預估發生了較大的偏差，同時它還會計算出RMS值，同樣反應了時間複雜度的偏差情況。

運行我們的測試：

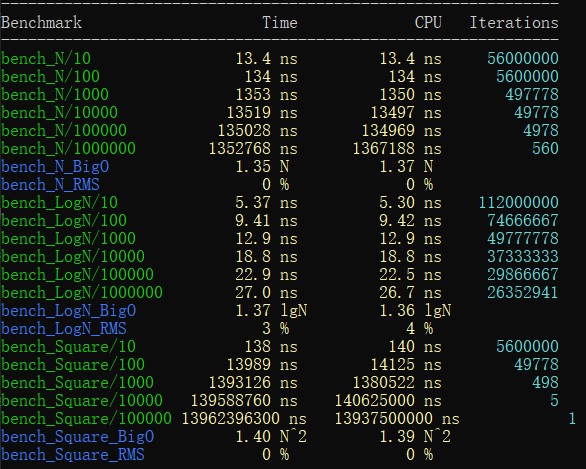
可以看到，自動的時間複雜度計算基本是準確的，可以在我們對演算法進行測試時提供一個有效的參考。