常見排序演算法（三）

計數排序：

 　　1、一個非基於比較的排序演算法，該演算法於1954年由 Harold H. Seward 提出，它的優勢在於在對一定範圍內的整數排序，

　　　  其時間複雜度為Ο(n+k)（其中k是整數的範圍），快於任何比較排序演算法

　　2、步驟：

　　　　a、找出給定整數序列的最大值 max 和最小值 min，創建大小為 max-min+1 的輔助空間，其值為 0

　　　　b、最小的那個數下標為 0，最大數下標為 -1，其他數 num 的下標為 num-min

　　　　c、根據遍歷所找到的數，在其相應下標處的值加一

　　　　d、遍歷輔助空間，輸出對應下標的數，其輸出次數為下標處的值，即若輔助空間 temp[0] == 5，則輸出下標 0 對應的數 5 次

註：該演算法是以空間換時間，若待排序列不是整數，則最好不要使用，因為浮點數範圍比較大，即使像在 [0, 1) 這個區間也可以有極多個

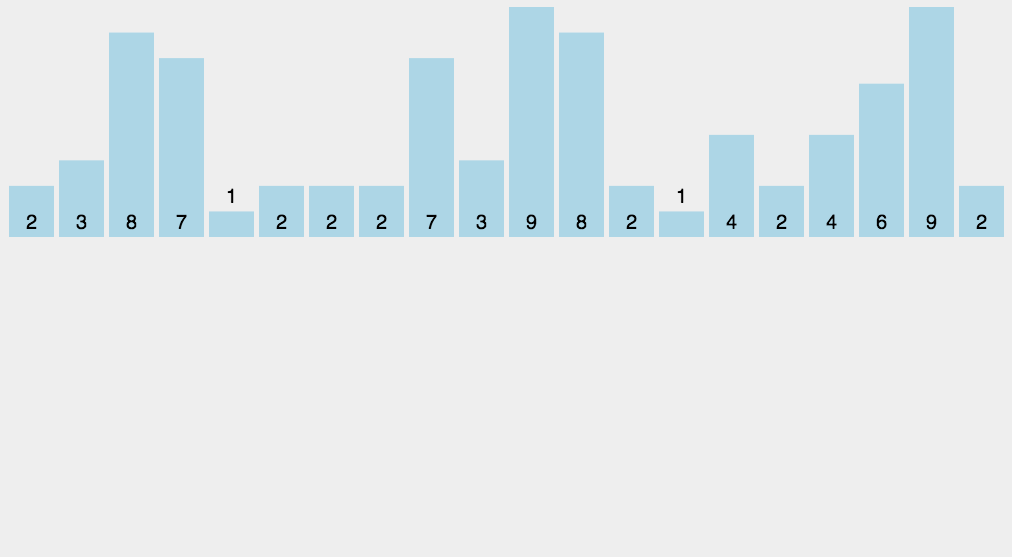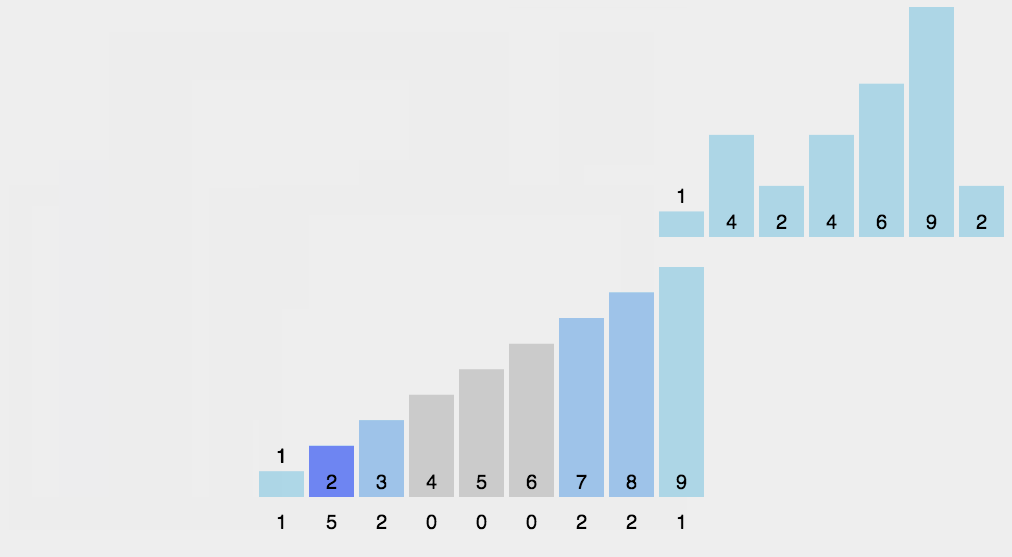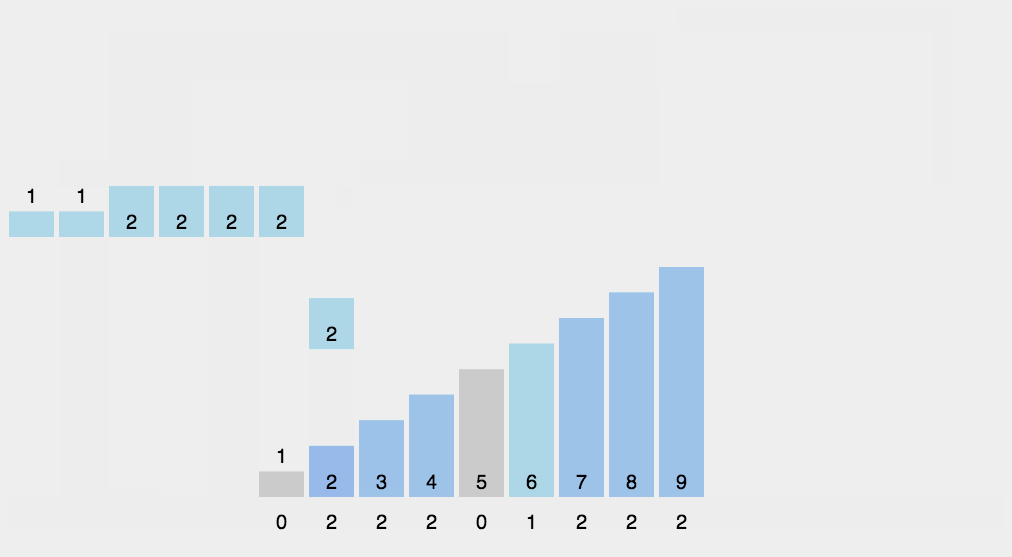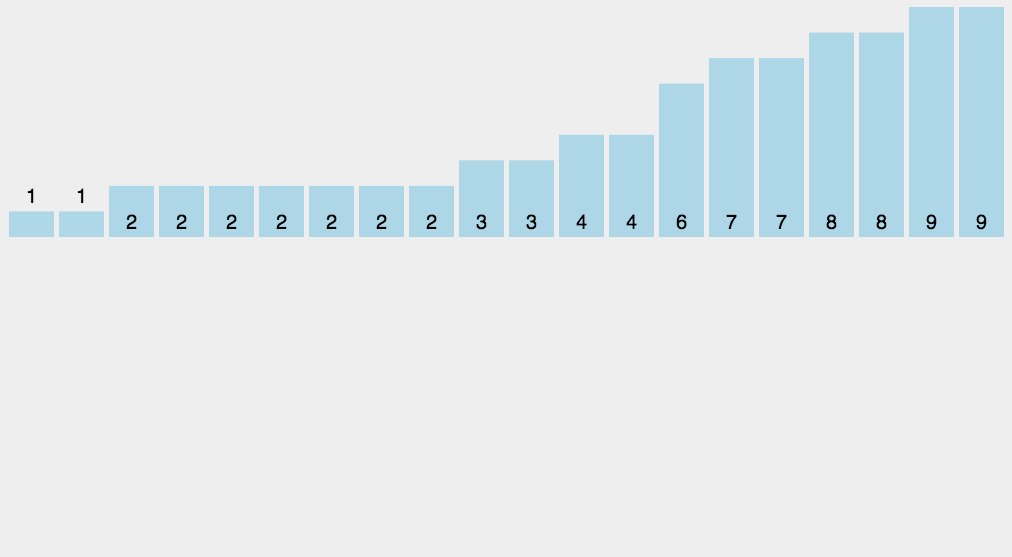
#include <iostream>
#include <vector>
#include <algorithm>

void countSort(std::vector<int>& nums);

int main()
{
    std::vector<int> nums;
    int len = 0;
    std::cout<<"請輸入長度：";
    do {
        std::cin>>len;
        if (len <= 0)
            std::cerr<<"請輸入正整數：";
    } while (len <= 0);
    int num = 0;
    std::cout<<"輸入 "<<len<<" 個數: ";
    for (size_t i = 0; i < len; ++i) {
        std::cin>>num;
        nums.push_back(num);
    }
    std::cout<<"排序後的數組：";
    countSort(nums);
    
    system("pause");
    
    return 0;
}

void countSort(std::vector<int>& nums)
{
//    註意要使用 '*' 號，因為它們找到的都是位置，這兩個函數都包含在 algorithm 裡面 
    int max = *max_element(nums.begin(), nums.end());
    int min = *min_element(nums.begin(), nums.end());
    int size = max - min + 1;
//    創建輔助空間，初始化為 0 
    std::vector<int> temp(size, 0);
//    將對應下標的數出現次數加一 
    for (auto num : nums)
        temp[num-min] += 1; 
    for (int i = 0; i < size; ++i) {
        int count = temp[i];
//        根據次數輸出，我們在這裡沒有改變原序列的順序，
//        僅僅輸出排序後的序列，若要改變原序列，需要執行複製操作 
        while (count > 0) {
            std::cout<<i+min<<std::ends;
            count--;
        }
    }
    std::cout<<std::endl;
}

基數排序：

 　　1、基數排序是根據待排序列的元素的位來進行排序的，是一種非比較排序；它可以分為兩類：

　　　   最低位優先法，簡稱 LSD 法：先從最低位開始排序，再對次低位排序，直到對最高位排序後得到一個有序序列

　　　   最高位優先法，簡稱 MSD 法：先從最高位開始排序，再逐個對各分組按次高位進行子排序，迴圈直到最低位

　　　   以下是 LSD 的動態演示圖

　　2、步驟（LSD）：

　　　　a、根據待排序的元素的最多位數確定迴圈次數，如最多位的數位 12345，則迴圈 5 次

　　　　b、創建 10 張空表，分別表示 0~9

　　　　c、從最低位開始，根據位上的數值選擇放入的表，如 123 在最低位上的數為 3，則放到下標為 3 的表裡

　　　　d、按順序將表裡的元素取出，替換原序列的數

　　　　e、向高移動一位，重覆操作 c 和 d，直至迴圈次數

#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
#include <cstdlib> 

int get_times(int num);
int get_digit(int num, int d);
void radixSort(std::vector<int>& nums);

int main()
{
    std::vector<int> nums;
    int len = 0;
    std::cout<<"請輸入長度：";
    do {
        std::cin>>len;
        if (len <= 0)
            std::cerr<<"請輸入正整數：";
    } while (len <= 0);
    int num = 0;
    std::cout<<"輸入 "<<len<<" 個數: ";
    for (size_t i = 0; i < len; ++i) {
        std::cin>>num;
        nums.push_back(num);
    }
    radixSort(nums);
    std::cout<<"排序後的數組：";
    for (int num : nums)
        std::cout<<num<<std::ends;
    std::cout<<std::endl;
    
    system("pause");
    
    return 0;
}

// 獲取第 d 位的數值
int get_digit(int num, int d)
{
    return int(num / pow(10, d)) % 10;
}

// 獲取需要迴圈的次數
int get_times(int num)
{
    int times = 0;
    while (num) {
        times++;
        num /= 10;
    }
    return times;
}

//沒有考慮負數的情況，如果需要的話可以使用兩個數組，一個存放正數，一個存放負數 
void radixSort(std::vector<int>& nums)
{
    int max = *max_element(nums.begin(), nums.end());
    int times = get_times(max);
    int len = nums.size();
    
    for (size_t i = 0; i < times; ++i) {
        std::vector<std::vector<int>> temp(10);
        for (int num : nums) {
            temp[get_digit(num, i)].push_back(num);
        }
                // 清除數組內容
        nums.clear();
                // 賦值
        for (auto vec : temp) {
            for (int num : vec) {
                nums.push_back(num);
            }
        }
    }
    return ;
}

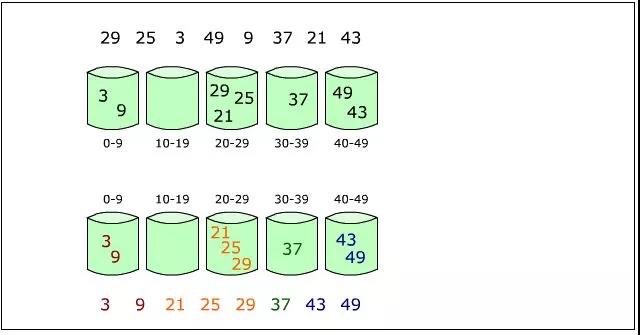
桶排序：

　　1、掃描選出待排序列的最大 max 和最小值 min，設有 k 個桶，則我們把區間 [min, max] 均勻地劃分為 k 個區間，

　　　  每個區間就是一個桶，然後再將待排序列地元素分配到各自的桶里，即數值的大小在哪個區間就分配到哪

　　2、對每個桶里的元素進行排序，可以選擇任意一種演算法

　　3、將各個桶里的元素合併成一個大的有序序列

#include <iostream>
#include <vector>
#include <cstdlib>
#include <algorithm>

void bucketSort(std::vector<int>& num);

int main()
{
    std::vector<int> nums;
    int len = 0;
    std::cout<<"請輸入長度：";
    do {
        std::cin>>len;
        if (len <= 0)
            std::cerr<<"請輸入正整數：";
    } while (len <= 0);
    int num = 0;
    std::cout<<"輸入 "<<len<<" 個數: ";
    for (size_t i = 0; i < len; ++i) {
        std::cin>>num;
        nums.push_back(num);
    }
    
    std::cout<<"排序後的數組：";
    bucketSort(nums);
    
    system("pause");
    
    return 0;
}

//這個排序我沒有改變原序列的順序，僅僅只是輸出有序序列，若要改變原序列，請添加賦值操作 
void bucketSort(std::vector<int>& nums)
{
//    尋找最大最小值 
    int max = *max_element(nums.begin(), nums.end());
    int min = *min_element(nums.begin(), nums.end());
    
//    為方便起見，桶個數直接採用範圍大小 
    int buckets_num = max-min+1;
    std::vector<std::vector<int>> res(buckets_num);
    
    for (int num : nums) {
//        按數壓入 
        res[num-min].push_back(num);
    }
    
    for (auto vec : res) {
//        桶內排序 
        sort(vec.begin(), vec.end());
    }
        
    for (auto vec : res)
        for (int num : vec)
            std::cout<<num<<std::ends;
    std::cout<<std::endl;
        
    return ;
}