圖的概念、存儲及遍歷 圖是一種特殊的數據結構,由點和邊構成,它可以用來描述元素之間的網狀關係,這個網狀沒有順序,也沒有層次,就是簡單的把各個元素連接起來。圖在我們的生活中也十分常見,地圖就是最簡單的例子。 圖的基本概念: 頂點集合為V,邊集合為E的圖記作G=(V,E)。另外,G=(V,E)的頂點數和 ...
圖的概念、存儲及遍歷
圖是一種特殊的數據結構,由點和邊構成,它可以用來描述元素之間的網狀關係,這個網狀沒有順序,也沒有層次,就是簡單的把各個元素連接起來。圖在我們的生活中也十分常見,地圖就是最簡單的例子。
圖的基本概念:
頂點集合為V,邊集合為E的圖記作G=(V,E)。另外,G=(V,E)的頂點數和邊數分別為|V|和|E|。對於兩個圖G和G',如果G'的頂點集合與邊集合均為G的頂點集合與邊集合的子集,那麼稱G'是G的子圖。子圖實際上就是一張圖裡面小一點的圖,也可以是點,不難理解。
有向圖:圖的邊有方向,只能按箭頭方向從一點到另一點。
無向圖:圖的邊沒有方向,可以雙向。
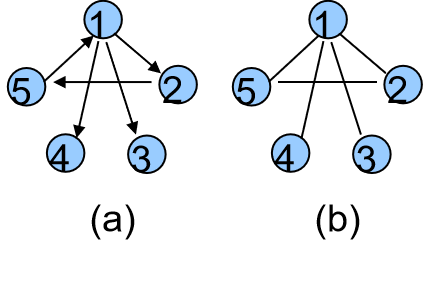
如圖,(a)就是有向圖,(b)就是無向圖。
頂點的度:無向圖中連著頂點的邊的數目。
頂點的入度和出度:有向圖中,以這個頂點為起點的邊的數量稱為這個頂點的出度;以這個頂點為終點的邊稱為這個頂點的入度。
邊權:邊的費用,可以形象的理解為“過路費”。對於一張存在邊權的圖,我們稱為“帶權圖”。
連通:如果圖中兩點U,V之間存在一條由U經過若幹邊、點到達V的路徑,則稱U,V是連通的。
迴路:起點和終點相同的路徑,稱為“迴路”或“環”。另外,不存在環的有向圖稱為Directed Acyclic Graph(DAG)。
完全圖:每個點都與其它所有的點有連邊的圖。
n個點的有向完全圖的邊數計算方法:每個點都可以自己為起點連出n-1條邊,因為除了它自己,剩下的n-1個點都能作為它連邊的終點,而整張圖有n個點,所以最終結果為:n(n-1)條邊;n個點的無向完全圖的邊數計算方法:因為是無向的,那麼a連到b、從b連到a這兩條邊只能算作一條,所以,無向完全圖的邊數應該是有向完全圖的一半,即:n(n-1)/2條。
稀疏圖:一張邊數遠遠少於完全圖的圖
稠密圖:一張邊數接近完全圖的圖
圖的存儲:
對於如何存儲一張圖,我們主要有三種方法。
(1)鄰接矩陣:對於一張圖來說,我們可以存儲點的信息,也可以存儲邊的信息,而鄰接矩陣存儲的是點的信息。對於一個點,我們需要知道的是它和哪些點有連邊,有時還要知道連邊的邊權。那麼,不難想到用二維數組來實現。
用map[u][v]來表示u和v 之間是否有連邊。如果u,v之間有連邊,那麼map[u][v]=1或邊權,如果是帶全圖就賦值邊權,否則賦值1;反之,賦值0或無窮大,如果是無向圖,就加上map[v][u]= map[u][v]。
對於帶權圖,我們極可能設計對整張圖的計算,所以要賦值邊權及無窮大,無窮大比無窮小要方便得多,因為在很多演算法中,我們需要邊權儘量小,如果賦值無窮小,那不是優先選這條實際上不存在的邊了?還可以這樣想:我們的邊權相當於“過路費”,我們現在無法從u到達v,你覺得是因為過路費太貴了還是過路費太便宜了?肯定是由於過路費太貴,我們付不起。這樣一想,就不難理解了。
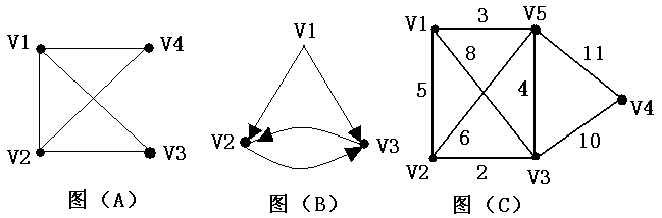
對於上面三幅圖,它們的鄰接矩陣分別如下:
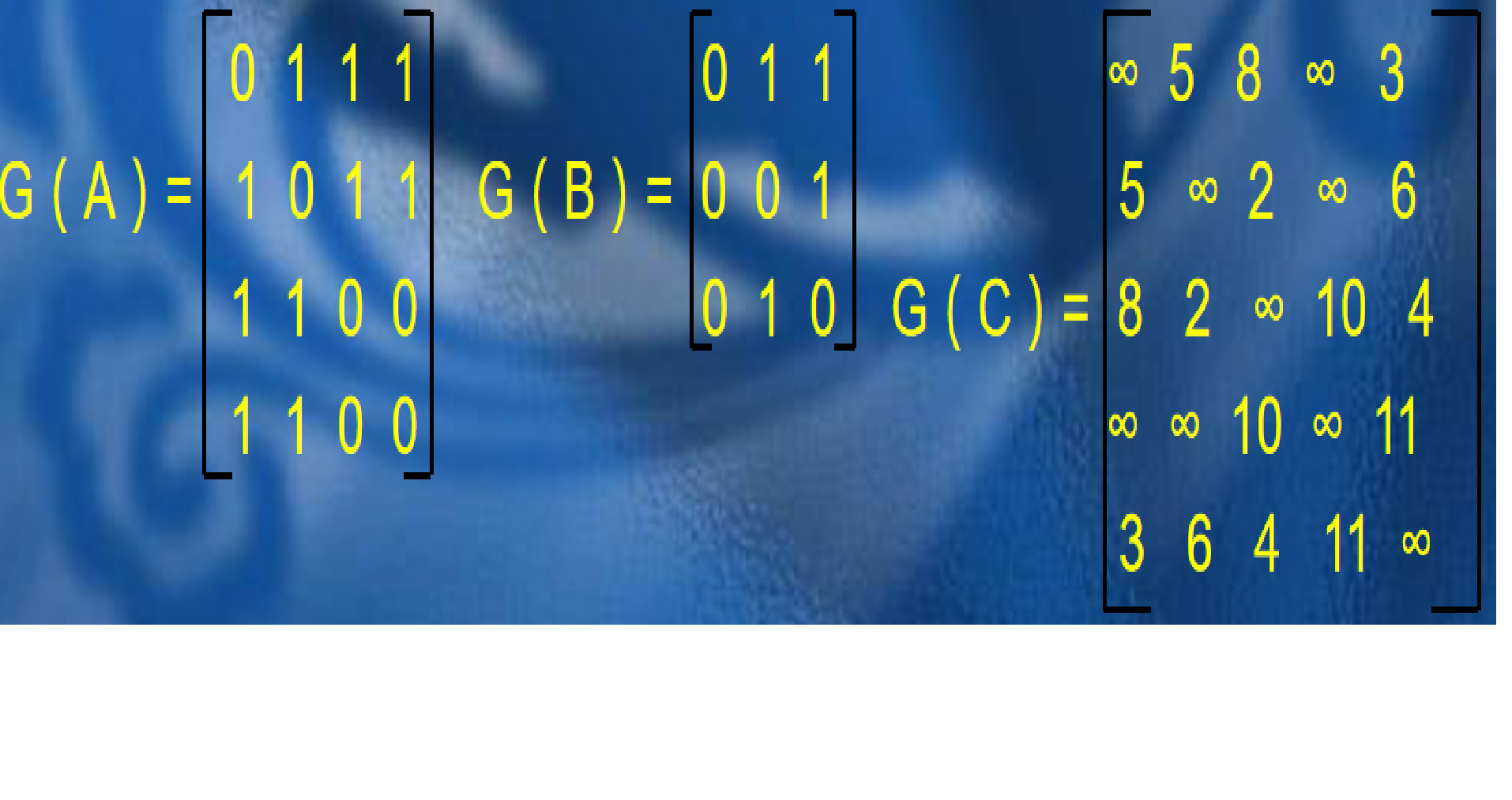
註意,鄰接矩陣不能存儲有重邊的圖,因為數組裡的每一個位置只能記錄一個值。那麼,鄰接矩陣的空間複雜度就是O(n2),n為點數,添加及查詢邊的複雜度均為O(1)。這種方式適合存儲稠密圖,因為它申請的空間是準備用來存儲每個點到其它所有點的邊的邊權的,如果是稀疏圖,會造成很大的浪費。
代碼實現:
//有向圖
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
map[i][j]=0x7ffffff;
for(i=1;i<=n;i++)map[i][i]=0;
for(i=1;i<=e;i++)
{
scanf("%d%d%d",&u,&v,&w);
map[u][v]=w;
}(2)邊集數組:除了存儲點的信息,我們還可以存儲邊的信息。對於一條邊,我們需要知道它的起點、終點以及邊權,那麼,我們不難想到可以用結構體來存儲。這種存儲方式非常簡單粗暴,適用於對邊依次進行處理,但不適用於對頂點的處理和對任意一條邊的處理,因為邊集數組查詢邊的複雜度為O(e),e為邊數,這個不難理解,因為我們需要遍歷整個數組。如果要處理頂點,那麼每一次頂點的拓展都要花費O(e)的時間,時間複雜度非常大,而每次查找任意一條邊也要花費O(e)的時間,所以均不適用。如果是對邊的順次處理,那來一遍迴圈就ok了。
從空間上來看,邊集數組適用於稀疏圖,因為要存儲每一條邊,所以邊集數組的空間複雜度為O(e),插入邊的複雜度為O(1)。根據上面說的完全圖邊數的計算方法,即使是無向圖,當n=10000時,完全圖的邊數也達到了49995000,完全存不下,因此適用於稀疏圖。
代碼實現:
for(i=1;i<=e;i++)
{
scanf("%d%d%d",&u,&v,&w);
e[i].u=u;
e[i].v=v;
e[i].len=w;
}(3)鄰接表:邊集數組的缺陷在於邊與邊之間沒有聯繫,那我們想辦法將邊聯繫起來。能聯繫在一起的邊,必然要有什麼共同點,我們不妨讓它們的某個東西相同。什麼東西相同呢?邊權嗎?把邊權相等的邊放在一起對我們沒有任何幫助。本質上,我們對邊集數組的不滿在於它無法快速地進行點的拓展,第一它不知道這個點連出了哪些邊,第二它也不知道連出了幾條,這才是最要命的。
問題很明確,我們需要快速地知道一個點連出的邊,那我們不妨把它們放在一起。別忘了,我們還需要很快地知道這個點連出的一條邊的下一條邊。有點拗口,我們不妨一個點連出的邊編號1、2、3,我們需要快速地知道1下一條是2,2下一條是3,這樣的形式,我們可以採用鏈表的形式來存儲。將同一個頂點連出的邊鏈接在同一個邊鏈表中,鏈表裡的每一個點代表一條邊,這個點叫做邊結點。
現在,我們要記錄的每個邊結點的信息稍有變動:我們要記錄這條邊的終點,這條邊的邊權,以及這條邊的上一條邊,因為我們採用的是鏈表的形式,所以要記錄前驅,當然你也可以抽象地理解為:這條邊的下一跳邊,因為實現的時候處理完這條邊下一個就處理我們記錄的這下(上)一條邊了,這個操作依然可以用結構體實現。然後,我們還要記錄每個點連出的最後一條邊,同樣可以抽象理解為第一條邊。這樣,我們每次拿到這個點連出的第一條邊,然後順著第一條慢慢往下拿到第二條、第三條,時間複雜度均為O(),比邊集數組快飛了。
鄰接表的空間複雜度為O(n+e),我們可以算一下:首先,我們至少需要O(n)的數組來存放每個點連出邊的集合,然後我們又需讀入了e條邊,所以複雜度為O(n+e)。查詢邊的複雜度為O(Mi),Mi為由vi連出的邊的數目,插入邊的複雜度為O(1)。根據空間複雜度的計算,可以得出:鄰接表同樣適用於稀疏圖。
struct edge
{
int to,len,last;
}e[100001];//鄰接表
int first[10001];
//每個點連出的最後(第一)條邊
int len=0;//當前邊的總數,方便對邊的存儲
void add(int u,int v,int w)
{
len++;
e[len].to=v;
e[len].len=w;
e[len].last=first[u];
first[u]=len;
}三種方式的比較:
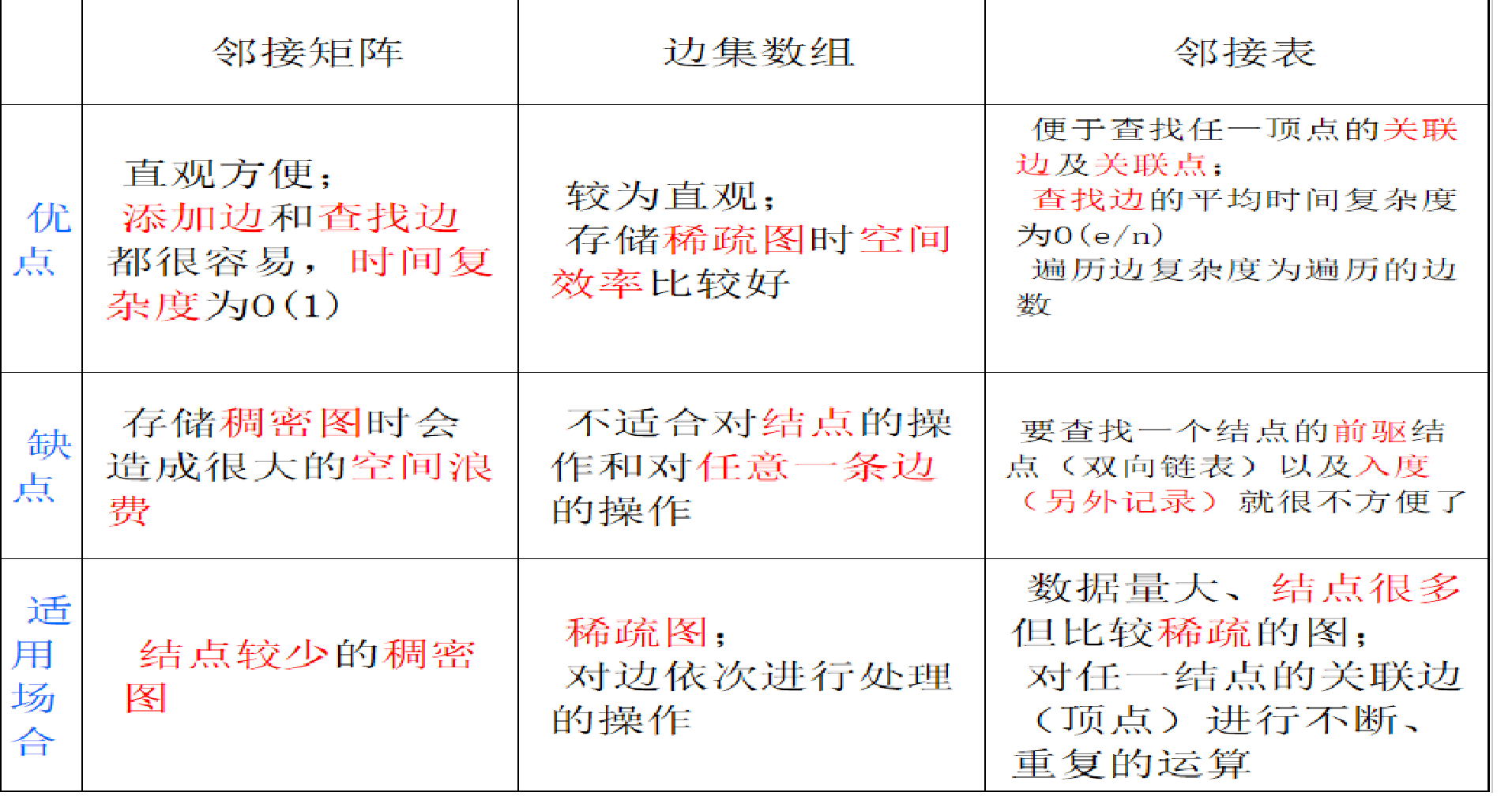
圖的遍歷:
我們想要對頂點進行操作,必然要對圖進行遍歷。圖的遍歷有兩種,都是我們耳熟能詳的:深度優先遍歷、廣度優先遍歷,具體的思想和搜索一模一樣,這裡不再重覆。
深度優先遍歷:
//鄰接表
void dfs(int dep)
{
blablabla......
int i;
for(i=first[dep];i;i=e[i].last)
if(b[a[i].to]==0)
{
b[a[i].to]=1;
dfs(a[i].to);
b[a[i].to]=0;
}
}廣度優先遍歷:
//鄰接表
void bfs()
{
int head=0,tail=1;
q[tail]=x;//x表示我們最開始的起點
b[x]=1;
while(head<tail)
{
head++;
int i,t=q[head];
for(i=first[t];i;i=a[i].last)
if(b[a[i].to]==0)
{
blablabla......
b[a[i].to]=1;
q[tail++]=a[i].to;
}
}
}


