P2711 小行星 (最大流)

題目

P2711 小行星

解析

這道題挺巧妙的，乍一看是空間上的，無從下手，稍微轉換一下就可以了。

看到題目，求消除這些行星的最少次數，就是求最小割，也就是求最大流，考慮怎樣建圖。

考慮當我們消去一個面上的所有點時，我們消去這個面後，這個面就不會再被消了，也就是只能被消一次，比如我們消去與\(\texttt{x=1}\)垂直的面上的點後，與\(\texttt{x=1}\)垂直的這個面就不會被再消一次，\(\texttt{y,z}\)同理。
但在這個面上的某些點（\(\texttt{x}\)相同，\(\texttt{y}\)，\(\texttt{z}\)不同的點）還會在另一些平面上，可能還會被再消。

直接連點的話會超時，我們考慮用點來代錶面(例如\(\texttt{x}\)中的1號點就代表與\(\texttt{x=1}\)垂直的面)，三個面就可以確定一個點，所以我們讓\(\texttt{x}\)與\(\texttt{y}\)與\(\texttt{z}\)相連，表示這個點。
我們這樣建圖
建立一個超級匯點\(\texttt{s}\)和超級源點\(\texttt{t}\)，\(\texttt{s}\)向所有\(\texttt{x}\)連邊，\(\texttt{x}\)向\(\texttt{y}\)連邊，\(\texttt{y}\)拆一下子點，拆完點出來向\(\texttt{z}\)連邊，所有\(\texttt{z}\)向\(\texttt{t}\)連邊。

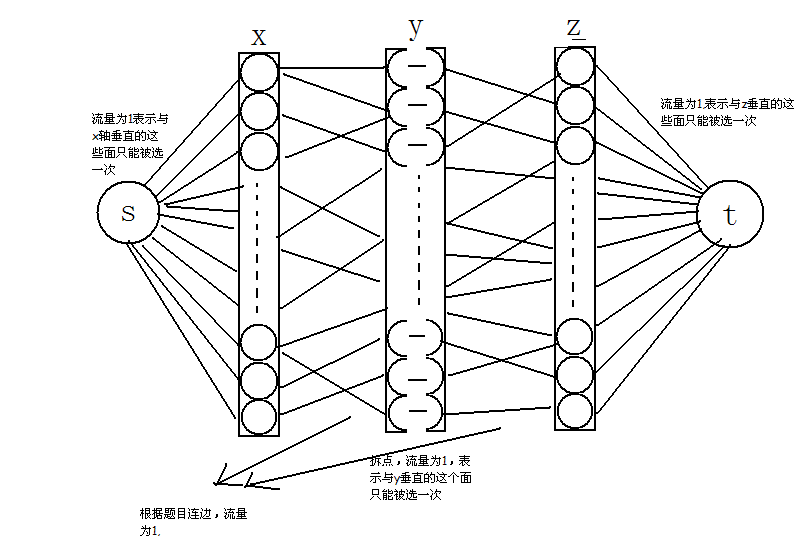
當我們某一條\(\texttt{s->x}\)的邊流滿時，就代表與\(\texttt{x}\)垂直的這個面被消掉了，\(\texttt{y->y'}\)流滿時表示與\(\texttt{y}\)垂直的這個面被消了，\(\texttt{z->t}\)流滿時表示與\(\texttt{z}\)垂直的這個面被消了，因為我們要求最小割，所以跑一遍最大流就行了。

代碼

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
const int INF = 0x3f3f3f3f;
int n, m, s, t, num = 1;
int head[N], cur[N], dep[N];
class node {
    public :
        int v, nx, w;
} e[N];

template<class T>inline void read(T &x) {
    x = 0; int f = 0; char ch = getchar();
    while (!isdigit(ch)) f |= (ch == '-'), ch = getchar();
    while (isdigit(ch)) x = x * 10 + ch - '0', ch = getchar();
    x = f ? -x : x;
    return ;
}

inline void add(int u, int v, int w) {
    e[++num].nx = head[u], e[num].v = v, e[num].w = w, head[u] = num;
    e[++num].nx = head[v], e[num].v = u, e[num].w = 0, head[v] = num;
}

queue<int>q;
bool bfs() {
    memset(dep, 0, sizeof dep);
    memcpy(cur, head, sizeof cur);
    dep[s] = 1;
    q.push(s);
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (int i = head[u]; ~i; i = e[i].nx) {
            int v = e[i].v;
            if (!dep[v] && e[i].w) dep[v] = dep[u] + 1, q.push(v);
        }
    }
    return dep[t];
}

int dfs(int u, int flow) {
    if (u == t) return flow;
    int use = 0;
    for (int &i = cur[u]; ~i; i = e[i].nx) {
        int v = e[i].v;
        if (e[i].w && dep[v] == dep[u] + 1) {
            int di = dfs(v, min(flow, e[i].w));
            e[i].w -= di, e[i ^ 1].w += di;
            use += di, flow -= di;
            if (flow <= 0) break;
        }
    }
    return use;
}

int dinic() {
    int ans = 0;
    while (bfs()) ans += dfs(s, INF);
    return ans;
}

int main() {
    memset(head, -1, sizeof head);
    read(n), read(m);
    for (int i = 1, x, y, z; i <= n; ++i) read(x), read(y), read(z), add(x, y, z);
    s = 1, t = m;
    printf("%d\n", dinic());
}