[TOC] 近期廣泛閱讀券商關於 巨集觀高頻數據 的研報,發現了兩點不足: 就研究手段而言,比較粗放,普遍停留在僅僅比較數據相關係數的層面; 就理論高度而言,很少探討數據背後的因果關聯。 不過有些理念先進的券商團隊已經開始從 產業鏈傳導 的角度試圖細緻的描述數據間的關聯,這正好契合了下麵這篇文章的核心 ...
目錄
近期廣泛閱讀券商關於巨集觀高頻數據的研報,發現了兩點不足:
- 就研究手段而言,比較粗放,普遍停留在僅僅比較數據相關係數的層面;
- 就理論高度而言,很少探討數據背後的因果關聯。
不過有些理念先進的券商團隊已經開始從產業鏈傳導的角度試圖細緻的描述數據間的關聯,這正好契合了下麵這篇文章的核心概念——有向無環圖(DAG)。
相關不是因果,哪又是啥?
本文翻譯自《"Correlation is not causation". So what is?》
鏈接:https://iyarlin.github.io/2019/02/08/correlation-is-not-causation-so-what-is/
導論
在過去幾年中,機器學習應用的數量和範圍都在迅速增長。什麼是因果推斷,它與傳統的 ML 有什麼不同?什麼時候應該考慮使用它?在本報告中,我嘗試通過一個例子給出一個簡短而具體的答案。
一個典型的數據科學課題
想象一下,營銷團隊的任務是找到提高營銷支出對銷售的影響。我們擁有營銷支出(mkt)、網站訪問(visits)、銷售(sales)和競爭指數(comp)的記錄。
我們將使用一組方程(也稱為結構方程)來模擬數據集:
\[ sales = \beta_1vists + \beta_2comp + \epsilon_1 \\ vists = \beta_3mkt + \epsilon_2\\ mkt = \beta_4comp + \epsilon_3\\ comp = \epsilon_4 \]
其中 \(\{\beta_1, \beta_2, \beta_3\, \beta_4\} = \{0.3, -0.9, 0.5, 0.6\}\).
下麵圖片中展示以及擬合模型用到的所有數據均由上面的等式模擬得到。
以下是數據集的前幾行:
| mkt | visits | sales | comp |
|---|---|---|---|
| 282.5 | 2977 | 379 | 3.635 |
| 338.8 | 3149 | 308 | 4.515 |
| 303.9 | 2485 | 369 | 3.092 |
| 558.8 | 3117 | 191 | 5.22 |
| 334.4 | 4038 | 286 | 4.281 |
| 297.7 | 2854 | 441 | 3.592 |
我們的目標是,得到預測營銷支出對銷售額的影響是 0.15 的結論(根據上面的方程組,對分項目做乘積,我們得到 \(\beta_1 \cdot \beta_3 = 0.3 \cdot 0.5 = 0.15\))。
常規分析方法
方法一:畫出雙變數關係
我們通常從畫出 sales 和 mkt 之間的散點圖開始:
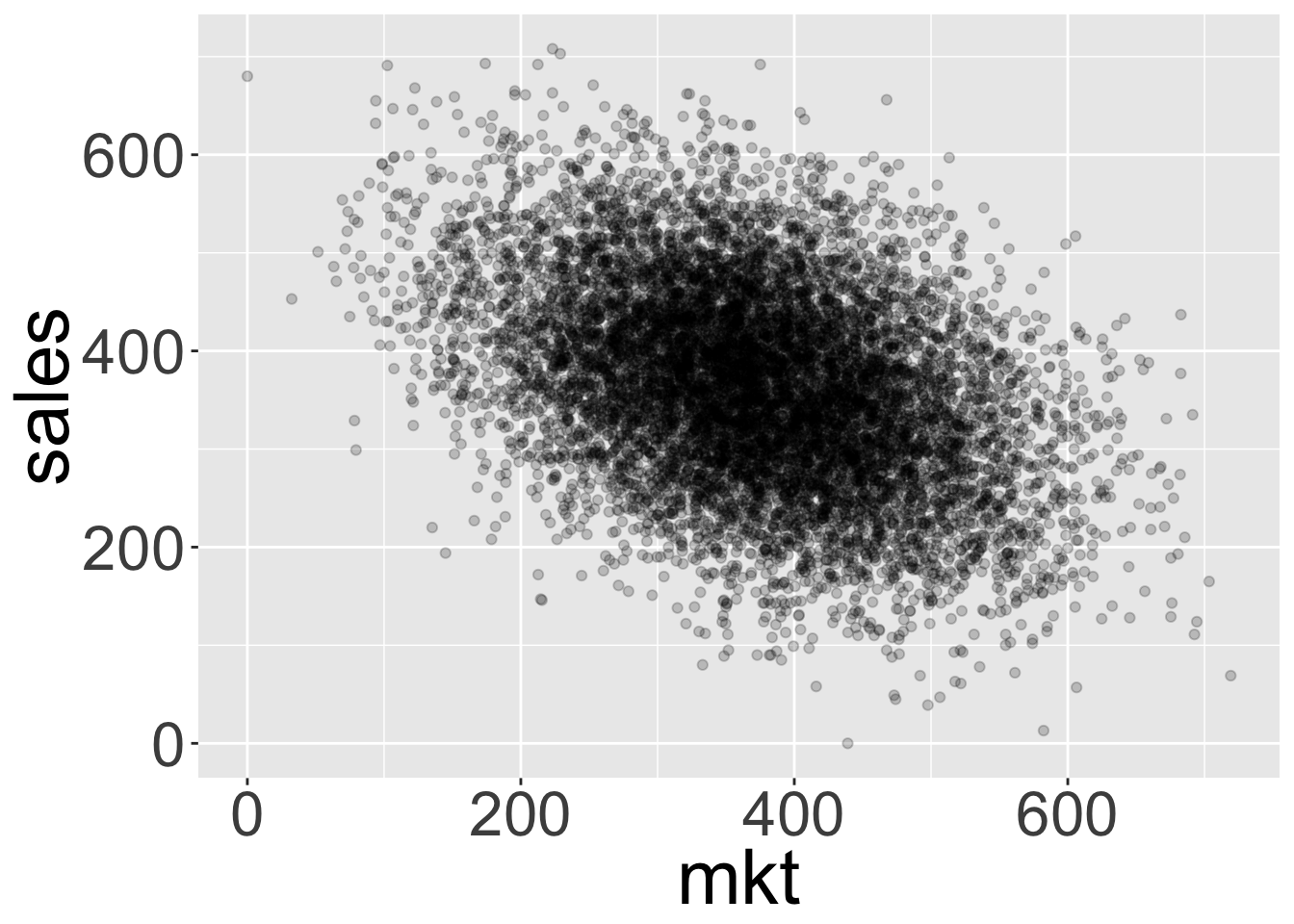
我們可以看到圖中看到的關係實際上與我們預期的相反!看起來增加營銷實際上會降低銷售額。實際上,不僅相關性不是因果關係,有時它可能表現出與真實因果關係相反的關係。
擬合一個簡單的線性模型 \(sales = r_0 + r_1mkt + \epsilon\) 將會產生下麵的繫數:(註意,\(r\) 泛指回歸繫數,而 \(\beta\) 泛指結構方程中真實的參數)
| (Intercept) | mkt |
|---|---|
| 513.5 | -0.3976 |
確認我們得到的效果與我們想要的效果截然不同(0.15)。
方法二:對所有可用特征使用 ML 模型
有人可能會假設,查看雙變數關係相當於僅使用 1 個預測變數,但如果我們要使用所有可用的特征,我們可能能夠找到更準確的估計。
運行回歸模型 \(sales = r_0 + r_1mkt + r_2visits + r_3comp + \epsilon\),得到下麵的繫數:
| (Intercept) | mkt | visits | comp |
|---|---|---|---|
| 596.7 | 0.009642 | 0.02849 | -90.06 |
現在看來營銷支出幾乎沒有任何影響!我們從線性方程模擬數據,並且我們知道即使使用更複雜的模型(例如 XGBoost、GAM)也無法產生更好的結果(我建議有疑慮的讀者通過重新運行 Rmd 腳本來嘗試一下生成報告)。
也許我們應該考慮下特征之間的關聯...
到目前為止我們獲得的結果相當令人困惑,我們進而咨詢營銷團隊,我們瞭解到,在競爭激烈的市場中,團隊通常會增加營銷支出(這反映在繫數 \(\beta_4 = 0.6\) 以上)。因此,競爭可能是一個“混雜”因數:當我們觀察到高營銷支出時,競爭也會很激烈,從而導致銷售額下降。
此外,我們註意到營銷可能會影響網站的訪問,而這些訪問又會影響銷售。
我們可以使用有向無環圖(DAG)可視化這些特征的相互依賴性:
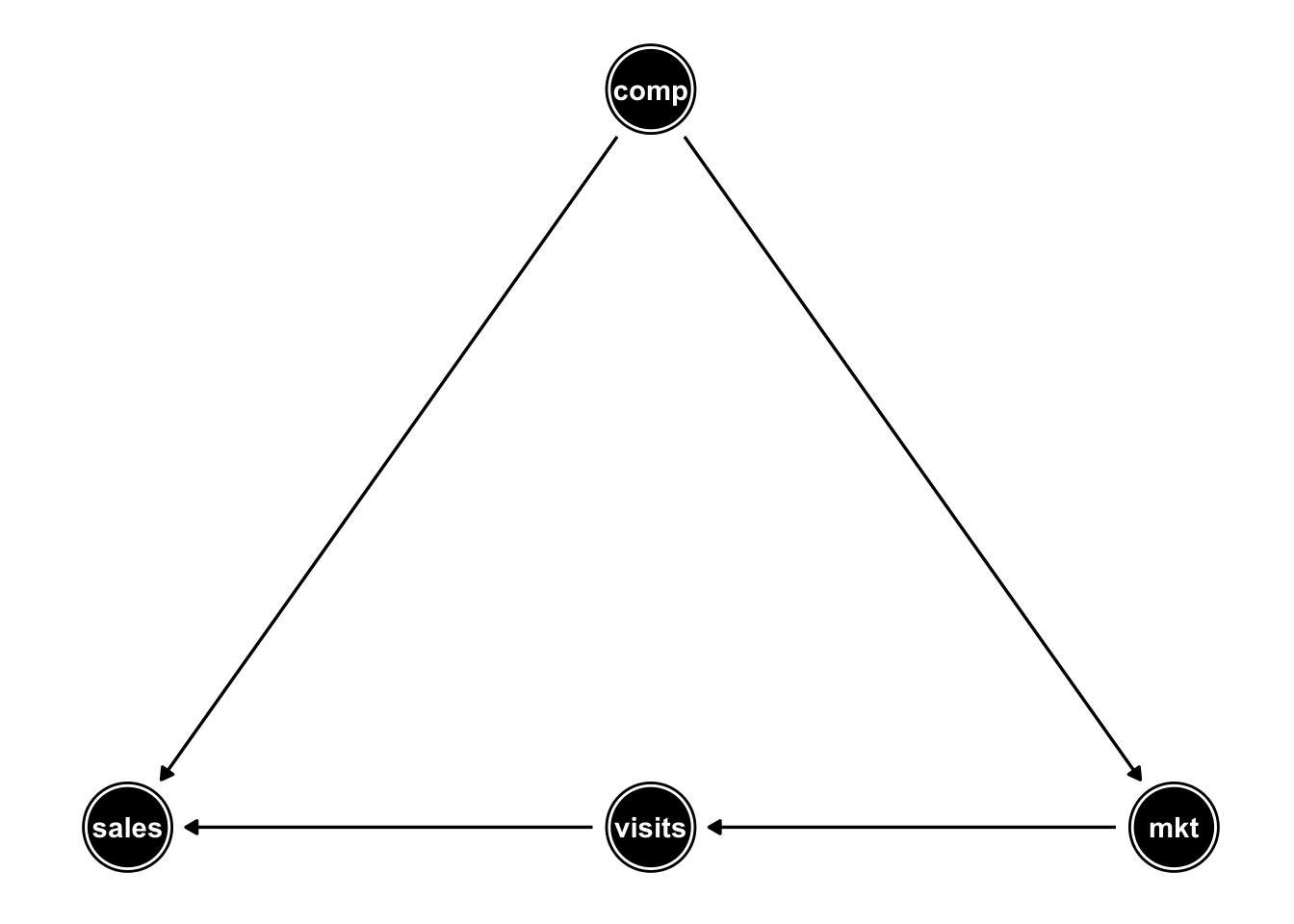
因此,通過將混雜競爭加到我們的回歸是有意義的。而在我們的模型中添加訪問可能會“屏蔽”或“消解”營銷對銷售的影響,所以我們應該從我們的模型中省略它。
運行回歸模型 \(sales = r_0 + r_1mkt + r_2comp + \epsilon\),得到下麵的繫數:
| (Intercept) | mkt | comp |
|---|---|---|
| 654.8 | 0.1494 | -89.8 |
現在我們終於得到了正確的效果估計!
我們解決問題的方式有點不穩健。我們提出了諸如特征的“混雜”和“屏蔽”等一般概念。試圖將這些應用於由數十個具有複雜關係的變數組成的數據集可能會非常困難。
所以現在做什麼?因果推斷!
到目前為止,我們已經看到,試圖通過檢查雙變數圖來估計營銷支出對銷售的影響可能會失敗。我們還看到,將所有可用特征拋入我們的標準 ML 模型也會失敗。看起來我們需要仔細構建模型中包含的協變數集,以獲得真實的效果。
在因果推斷中,該協變數集合也稱為“調整集”。給定模型的 DAG,我們可以利用各種演算法,這些演算法非常類似於上面提到的規則,例如“混雜”和“屏蔽”,以找到正確的調整集。
Backdoor Criteria 演算法
可以獲得正確調整集的最基本演算法之一是由 J. Pearl 開發的“Backdoor-criteria”。簡而言之,它尋求調整集,屏蔽“暴露”變數(例如營銷)和“結果”變數(例如銷售)之間的每一個“虛假”路徑,同時保持影響路徑存在。
考慮下麵的 DAG,我們試圖找到 x5 對 x10 的影響:

使用 backdoor-criterion 演算法(由 R 包 dagitty 實現),我們找到正確的調整集:

如何得到模型的 DAG?
誠然,找到模型的 DAG 非常有挑戰性。可以綜合考慮下列幾種方法:
- 藉助領域知識;
- 想給出一些候選 DAG,再用統計檢驗比較擬合水平;
- 使用搜索方法(藉助一些 R 包,例如
mgm或bnlearn)
我會在後面的文章中展開這些主題。
進階閱讀
想要進一步瞭解上述問題的朋友,我推薦閱讀 Pearl 寫的一篇輕量級的技術報告——《The Seven Tools of Causal Inference with Reflections on Machine Learning》。
想要深入瞭解因果推斷與 DAG 機制的話,我推薦 Pearl 的小冊子——《Causal Inference in Statistics - A Primer》。



