[toc] 在 R 中估計 GARCH 參數存在的問題(基於 rugarch 包) 本文翻譯自《Problems in Estimating GARCH Parameters in R (Part 2; rugarch)》 原文鏈接:https://ntguardian.wordpress.com/ ...
目錄
在 R 中估計 GARCH 參數存在的問題(基於 rugarch 包)
本文翻譯自《Problems in Estimating GARCH Parameters in R (Part 2; rugarch)》
原文鏈接:https://ntguardian.wordpress.com/2019/01/28/problems-estimating-garch-parameters-r-part-2-rugarch/
導論
這是一篇本應早就寫完的博客文章。一年前我寫了一篇文章,關於在 R 中估計 GARCH(1, 1) 模型參數時遇到的問題。我記錄了參數估計的行為(重點是 \(\beta\)),以及使用 fGarch 計算這些估計值時發現的病態行為。我在 R 社區呼籲幫助,包括通過 R Finance 郵件列表發送我的博客文章。
反饋沒有讓我感到失望。你可以看到一些郵件列表反饋,並且一些來自 Reddit 的評論也很有幫助,但我認為我得到的最佳反饋來自於我自己的電子郵件。
Dr. Brian G. Peterson 作為 R 金融社區的一員,給我發送了一些發人深思的電子郵件。首先,他告訴我 fGarch 不再是處理 GARCH 模型的首選方案。RMetrics 套件包(包括 fGarch)由 ETH Zürich 的 Diethelm Würtz 教授維護。他在 2016 年的車禍中喪生。
Dr. Peterson 建議我研究另外兩個用於 GARCH 建模的現代軟體包,rugarch(適用於單變數 GARCH 模型)和 rmgarch(適用於多變數 GARCH 模型)。之前我沒有聽說過這些包(我之所以知道 fGarch 的原因是因為它在由 Shumway 和 Stoffer 編寫的時間序列教科書——Time Series Analysis and Its Applications with R Examples 中),所以我非常感謝這個建議。由於我現在對單變數時間序列感興趣,所以我研究了 rugarch。該軟體包似乎具有比 fGarch 更多的功能和函數,這可以解釋為什麼它似乎更難以使用。然而,包的 vignette 很有幫助,值得列印出來。
Dr. Peterson 對我提出的應用也有一些有趣的評論。他認為,日內數據應優於日間數據,並且模擬數據(包括模擬 GARCH 過程)具有在實際數據中看不到的特質。獲取日間數據的便利性(特別是亞洲金融危機期間的 USD/JPY,這是我正在研究的檢驗統計量的預期應用)激發了我對日間數據的興趣。不過,他的評論可能會讓我重新考慮這個應用。1(我也許應該試圖通過 EUR/USD 來檢測 2010 年歐元區金融危機。為此,我可以從 HistData.com 獲得免費的日內數據。)但是,如果對於小樣本而言不能信任標準差的估計,我們的檢驗統計量仍然會遇到麻煩,因為它涉及小樣本的參數估計。
他還警告說,模擬數據表現出在實際數據中看不到的行為。這可能是真的,但模擬數據很重要,因為它可以被認為是統計學家的最佳情景。另外,生成模擬數據的過程的屬性是先驗已知的,包括生成參數的值,以及哪些假設(例如序列中是否存在結構變化)是真的。這允許對估計器和檢驗進行健全的檢查。這對現實世界來說是不可能的,因為我們沒有所需的先驗知識。
Prof. André Portela Santos 要求我重覆模擬,但使用 \(\alpha = 0.6\),因為這些值比我選擇的 \(\alpha = \beta = 0.2\) 更常見。這是一個很好的建議,除了 \(\alpha = \beta = 0.2\) 之外,我還會在博文里考慮此範圍內的參數。然而,我的模擬暗示當 \(\alpha = \beta = 0.2\) 時,估計演算法似乎想要接近較大的 \(\beta\)。我也很驚訝,因為我的導師給我的印象是,\(\alpha\) 或 \(\beta\) 大的 GARCH 過程更難以處理。最後,如果估計量嚴重有偏,我們可能會看到大多數估計參數位於該範圍內,但這並不意味著“正確”值位於該範圍內。我的模擬顯示 fGarch 很難發現 \(\alpha = \beta = 0.2\),即使這些參數是“真的”。Prof. Santos 的評論讓我想要做一個在真實世界中 GARCH 參數的估計是什麼樣子的元研究(metastudy)。(可能有也可能沒有,我沒有檢查過。如果有人知道,請分享。)
我的導師聯繫了另一位 GARCH 模型的專家,並獲得了一些反饋。據推測,\(\beta\) 的標準差很大,因此參數估計應該有很大的變動範圍。即使對於小樣本,我的一些模擬也認同這種行為,但同時顯示出對 \(\beta = 0\) 和 \(\beta = 1\) 令人不舒服的偏向。正如我假設的那樣,這可能是優化程式的結果。
因此,鑒於此反饋,我將進行更多的模擬實驗。我不會再研究 fGarch 或 tseries 了,我將專門研究 rugarch。我將探討包支持的不同優化程式。我不會像我在第一篇文章中那樣畫圖,這些圖只是為了表明存在的問題及其嚴重性。相反,我將考察由不同優化程式生成的估計器的特性。
rugarch 簡介
如上所述,rugarch 是一個用於處理 GARCH 模型的軟體包,一個主要的用例顯然是估計模型的參數。在這裡,我將演示如何指定 GARCH 模型、模擬模型的數據以及估計參數。在此之後,我們可以深入瞭解模擬研究。
library(rugarch)## Loading required package: parallel
##
## Attaching package: 'rugarch'
## The following object is masked from 'package:stats':
##
## sigma指定一個 \(\text{GARCH}(1, 1)\) 模型
要使用 GARCH 模型,我們需要指定它。執行此操作的函數是 ugarchspec()。我認為最重要的參數是 variance.model 和 mean.model。
variance.model 是一個命名列表,也許最感興趣的兩個元素是 model 和 garchOrder。model 是一個字元串,指定擬合哪種類型的 GARCH 模型。包支持許多主要的 GARCH 模型(例如 EGARCH、IGARCH 等),對於“普通”GARCH 模型,要將其設置為 sGARCH(或者只是忽略它,標準模型是預設的)。garchOrder 是模型中 ARCH 和 GARCH 部分的階數向量。
mean.model 允許擬合 ARMA-GARCH 模型,並且像 variance.model 一樣接受一個命名列表,最感興趣的參數是 armaOrder 和 include.mean。armaOrder 就像 garchOrder,它是一個指定 ARMA 模型階數的向量。include.mean 是一個布爾值,如果為 true,則允許模型的 ARMA 部分具有非零均值。
在模擬過程時,我們需要設置參數的值。這是通過 fixed.pars 參數完成的,該參數接受命名列表,列表的元素是數字。它們需要符合函數對於參數的約定。例如,如果我們想設置 \(\text{GARCH}(1,1)\) 模型的參數,我們列表元素的名稱應該是 alpha1 和 beta1。如果計劃是模擬一個模型,則應以這種方式設置模型中的每個參數。
還有其他有趣的參數,但我只關註這些,因為預設指定是 ARMA-GARCH 模型,ARMA 階數為 \((1,1)\),非零均值,並且 GARCH 模型的階數是 \((1, 1)\)。這不是我想要的普通 \(\text{GARCH}(1,1)\) 模型,所以我幾乎總是要修改它。
spec1 <- ugarchspec(
mean.model = list(
armaOrder = c(0,0), include.mean = FALSE),
fixed.pars = list(
"omega" = 0.2, "alpha1" = 0.2, "beta1" = 0.2))
spec2 <- ugarchspec(
mean.model = list(
armaOrder = c(0,0), include.mean = FALSE),
fixed.pars = list(
"omega" = 0.2, "alpha1" = 0.1, "beta1" = 0.7))
show(spec1)##
## *---------------------------------*
## * GARCH Model Spec *
## *---------------------------------*
##
## Conditional Variance Dynamics
## ------------------------------------
## GARCH Model : sGARCH(1,1)
## Variance Targeting : FALSE
##
## Conditional Mean Dynamics
## ------------------------------------
## Mean Model : ARFIMA(0,0,0)
## Include Mean : FALSE
## GARCH-in-Mean : FALSE
##
## Conditional Distribution
## ------------------------------------
## Distribution : norm
## Includes Skew : FALSE
## Includes Shape : FALSE
## Includes Lambda : FALSEshow(spec2)##
## *---------------------------------*
## * GARCH Model Spec *
## *---------------------------------*
##
## Conditional Variance Dynamics
## ------------------------------------
## GARCH Model : sGARCH(1,1)
## Variance Targeting : FALSE
##
## Conditional Mean Dynamics
## ------------------------------------
## Mean Model : ARFIMA(0,0,0)
## Include Mean : FALSE
## GARCH-in-Mean : FALSE
##
## Conditional Distribution
## ------------------------------------
## Distribution : norm
## Includes Skew : FALSE
## Includes Shape : FALSE
## Includes Lambda : FALSE模擬一個 GARCH 過程
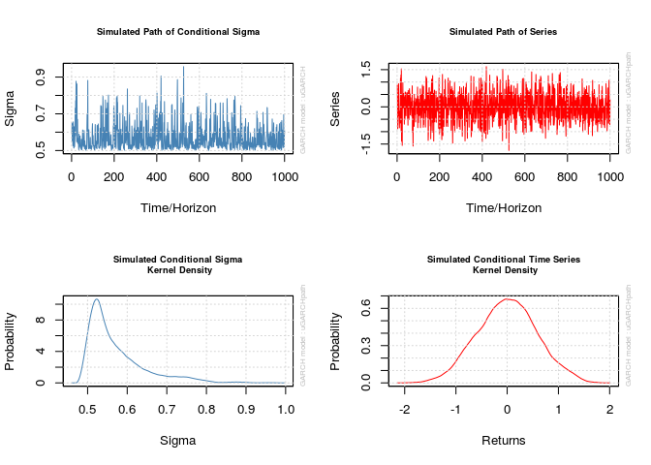
函數 ugarchpath() 模擬由 ugarchspec() 指定的 GARCH 模型。該函數首先需要由 ugarchspec() 創建的指定對象。參數 n.sim 和 n.start 分別指定過程的大小和預熱期的長度(分別預設為 1000 和 0。我強烈建議將預熱期設置為至少 500,但我設置為 1000)。該函數創建的對象不僅包含模擬序列,還包含殘差和 \(\sigma_t\)。
rseed 參數控制函數用於生成數據的隨機種子。請註意,此函數會有效地忽略 set.seed(),因此如果需要一致的結果,則需要設置此參數。
這些對象相應的 plot() 方法並不完全透明。它可以創建一些圖,當在命令行中對 uGARCHpath 對象調用 plot() 時,系統會提示用戶輸入與所需圖形對應的數字。這有時挺痛苦,所以不要忘記將所需的編號傳遞給 which 參數以避免提示,設置 which = 2 將正好給出序列的圖。
old_par <- par()
par(mfrow = c(2, 2))
x_obj <- ugarchpath(
spec1, n.sim = 1000, n.start = 1000, rseed = 111217)
show(x_obj)##
## *------------------------------------*
## * GARCH Model Path Simulation *
## *------------------------------------*
## Model: sGARCH
## Horizon: 1000
## Simulations: 1
## Seed Sigma2.Mean Sigma2.Min Sigma2.Max Series.Mean
## sim1 111217 0.332 0.251 0.915 0.000165
## Mean(All) 0 0.332 0.251 0.915 0.000165
## Unconditional NA 0.333 NA NA 0.000000
## Series.Min Series.Max
## sim1 -1.76 1.62
## Mean(All) -1.76 1.62
## Unconditional NA NAfor (i in 1:4)
{
plot(x_obj, which = i)
}
par(old_par)## Warning in par(old_par): graphical parameter "cin" cannot be set
## Warning in par(old_par): graphical parameter "cra" cannot be set
## Warning in par(old_par): graphical parameter "csi" cannot be set
## Warning in par(old_par): graphical parameter "cxy" cannot be set
## Warning in par(old_par): graphical parameter "din" cannot be set
## Warning in par(old_par): graphical parameter "page" cannot be set# The actual series
x1 <- x_obj@path$seriesSim
plot.ts(x1)
擬合一個 \(\text{GARCH}(1,1)\) 模型
ugarchfit() 函數擬合 GARCH 模型。該函數需要指定和數據集。solver 參數接受一個字元串,說明要使用哪個數值優化器來尋找參數估計值。函數的大多數參數管理數值優化器的介面。特別是,solver.control 可以接受一個傳遞給優化器的參數列表。我們稍後會更詳細地討論這個問題。
用於生成模擬數據的指定將不適用於 ugarchfit(),因為它包含其參數的固定值。在我的情況下,我將需要創建第二個指定對象。
spec <- ugarchspec(
mean.model = list(armaOrder = c(0, 0), include.mean = FALSE))
fit <- ugarchfit(spec, data = x1)
show(fit)##
## *---------------------------------*
## * GARCH Model Fit *
## *---------------------------------*
##
## Conditional Variance Dynamics
## -----------------------------------
## GARCH Model : sGARCH(1,1)
## Mean Model : ARFIMA(0,0,0)
## Distribution : norm
##
## Optimal Parameters
## ------------------------------------
## Estimate Std. Error t value Pr(>|t|)
## omega 0.000713 0.001258 0.56696 0.57074
## alpha1 0.002905 0.003714 0.78206 0.43418
## beta1 0.994744 0.000357 2786.08631 0.00000
##
## Robust Standard Errors:
## Estimate Std. Error t value Pr(>|t|)
## omega 0.000713 0.001217 0.58597 0.55789
## alpha1 0.002905 0.003661 0.79330 0.42760
## beta1 0.994744 0.000137 7250.45186 0.00000
##
## LogLikelihood : -860.486
##
## Information Criteria
## ------------------------------------
##
## Akaike 1.7270
## Bayes 1.7417
## Shibata 1.7270
## Hannan-Quinn 1.7326
##
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 3.998 0.04555
## Lag[2*(p+q)+(p+q)-1][2] 4.507 0.05511
## Lag[4*(p+q)+(p+q)-1][5] 9.108 0.01555
## d.o.f=0
## H0 : No serial correlation
##
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 29.12 6.786e-08
## Lag[2*(p+q)+(p+q)-1][5] 31.03 1.621e-08
## Lag[4*(p+q)+(p+q)-1][9] 32.26 1.044e-07
## d.o.f=2
##
## Weighted ARCH LM Tests
## ------------------------------------
## Statistic Shape Scale P-Value
## ARCH Lag[3] 1.422 0.500 2.000 0.2331
## ARCH Lag[5] 2.407 1.440 1.667 0.3882
## ARCH Lag[7] 2.627 2.315 1.543 0.5865
##
## Nyblom stability test
## ------------------------------------
## Joint Statistic: 0.9518
## Individual Statistics:
## omega 0.3296
## alpha1 0.2880
## beta1 0.3195
##
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic: 0.846 1.01 1.35
## Individual Statistic: 0.35 0.47 0.75
##
## Sign Bias Test
## ------------------------------------
## t-value prob sig
## Sign Bias 0.3946 6.933e-01
## Negative Sign Bias 3.2332 1.264e-03 ***
## Positive Sign Bias 4.2142 2.734e-05 ***
## Joint Effect 28.2986 3.144e-06 ***
##
##
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
## group statistic p-value(g-1)
## 1 20 20.28 0.3779
## 2 30 26.54 0.5965
## 3 40 36.56 0.5817
## 4 50 47.10 0.5505
##
##
## Elapsed time : 2.60606par(mfrow = c(3, 4))
for (i in 1:12)
{
plot(fit, which = i)
}##
## please wait...calculating quantiles...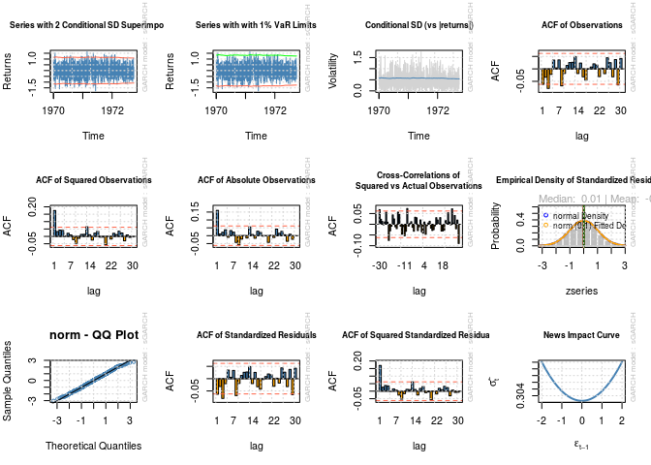
par(old_par)## Warning in par(old_par): graphical parameter "cin" cannot be set
## Warning in par(old_par): graphical parameter "cra" cannot be set
## Warning in par(old_par): graphical parameter "csi" cannot be set
## Warning in par(old_par): graphical parameter "cxy" cannot be set
## Warning in par(old_par): graphical parameter "din" cannot be set
## Warning in par(old_par): graphical parameter "page" cannot be set註意估計的參數和標準差?即使對於 1000 的樣本大小,估計也與“正確”數字相去甚遠,並且基於估計標準差的合理置信區間不包含正確的值。看起來我在上一篇文章中記錄的問題並沒有消失。
出於好奇,在 Prof. Santos 建議範圍的其他指定會發生什麼?
x_obj <- ugarchpath(
spec2, n.start = 1000, rseed = 111317)
x2 <- x_obj@path$seriesSim
fit <- ugarchfit(spec, x2)
show(fit)##
## *---------------------------------*
## * GARCH Model Fit *
## *---------------------------------*
##
## Conditional Variance Dynamics
## -----------------------------------
## GARCH Model : sGARCH(1,1)
## Mean Model : ARFIMA(0,0,0)
## Distribution : norm
##
## Optimal Parameters
## ------------------------------------
## Estimate Std. Error t value Pr(>|t|)
## omega 0.001076 0.002501 0.43025 0.66701
## alpha1 0.001992 0.002948 0.67573 0.49921
## beta1 0.997008 0.000472 2112.23364 0.00000
##
## Robust Standard Errors:
## Estimate Std. Error t value Pr(>|t|)
## omega 0.001076 0.002957 0.36389 0.71594
## alpha1 0.001992 0.003510 0.56767 0.57026
## beta1 0.997008 0.000359 2777.24390 0.00000
##
## LogLikelihood : -1375.951
##
## Information Criteria
## ------------------------------------
##
## Akaike 2.7579
## Bayes 2.7726
## Shibata 2.7579
## Hannan-Quinn 2.7635
##
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 0.9901 0.3197
## Lag[2*(p+q)+(p+q)-1][2] 1.0274 0.4894
## Lag[4*(p+q)+(p+q)-1][5] 3.4159 0.3363
## d.o.f=0
## H0 : No serial correlation
##
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 3.768 0.05226
## Lag[2*(p+q)+(p+q)-1][5] 4.986 0.15424
## Lag[4*(p+q)+(p+q)-1][9] 7.473 0.16272
## d.o.f=2
##
## Weighted ARCH LM Tests
## ------------------------------------
## Statistic Shape Scale P-Value
## ARCH Lag[3] 0.2232 0.500 2.000 0.6366
## ARCH Lag[5] 0.4793 1.440 1.667 0.8897
## ARCH Lag[7] 2.2303 2.315 1.543 0.6686
##
## Nyblom stability test
## ------------------------------------
## Joint Statistic: 0.3868
## Individual Statistics:
## omega 0.2682
## alpha1 0.2683
## beta1 0.2669
##
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic: 0.846 1.01 1.35
## Individual Statistic: 0.35 0.47 0.75
##
## Sign Bias Test
## ------------------------------------
## t-value prob sig
## Sign Bias 0.5793 0.5625
## Negative Sign Bias 1.3358 0.1819
## Positive Sign Bias 1.5552 0.1202
## Joint Effect 5.3837 0.1458
##
##
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
## group statistic p-value(g-1)
## 1 20 24.24 0.1871
## 2 30 30.50 0.3894
## 3 40 38.88 0.4753
## 4 50 48.40 0.4974
##
##
## Elapsed time : 2.841597沒有更好。現在讓我們看看當我們使用不同的優化演算法時會發生什麼。
rugarch 中的優化與參數估計
優化器的選擇
ugarchfit() 的預設參數很好地找到了我稱之為模型 2 的適當參數(其中 \(\alpha = 0.1\) 和 \(\beta = 0.7\)),但不適用於模型 1(\(\alpha = \beta = 0.2\))。我想知道的是何時一個求解器能擊敗另一個求解器。
正如 Vivek Rao2 在 R-SIG-Finance 郵件列表中所說,“最佳”估計是最大化似然函數(或等效地,對數似然函數)的估計,在上一篇文章中我忽略了檢查對數似然函數值。在這裡,我將看到哪些優化程式導致最大對數似然。
下麵是一個輔助函數,它簡化了擬合 GARCH 模型參數、提取對數似然、參數值和標準差的過程,同時允許將不同的值傳遞給 solver 和 solver.control。
evalSolverFit <- function(spec, data,
solver = "solnp",
solver.control = list())
{
# Calls ugarchfit(spec, data, solver, solver.control), and returns a vector
# containing the log likelihood, parameters, and parameter standard errors.
# Parameters are equivalent to those seen in ugarchfit(). If the solver fails
# to converge, NA will be returned
vec <- NA
tryCatch(
{
fit <- ugarchfit(
spec = spec,
data = data,
solver = solver,
solver.control = solver.control)
coef_se_names <- paste(
"se", names(fit@fit$coef), sep = ".")
se <- fit@fit$se.coef
names(se) <- coef_se_names
robust_coef_se_names <- paste(
"robust.se", names(fit@fit$coef), sep = ".")
robust.se <- fit@fit$robust.se.coef
names(robust.se) <- robust_coef_se_names
vec <- c(fit@fit$coef, se, robust.se)
vec["LLH"] <- fit@fit$LLH
},
error = function(w) { NA })
return(vec)
}下麵我列出將要考慮的所有優化方案。我只使用 solver.control,但可能有其他參數可以幫助數值優化演算法,即 numderiv.control,它們作為控制參數傳遞給負責標準差計算的數值演算法。這利用了包含 numDeriv 的包,它執行數值微分。
solvers <- list(
# A list of lists where each sublist contains parameters to
# pass to a solver
list("solver" = "nlminb", "solver.control" = list()),
list("solver" = "solnp", "solver.control" = list()),
list("solver" = "lbfgs", "solver.control" = list()),
list("solver" = "gosolnp",
"solver.control" = list("n.restarts" = 100, "n.sim" = 100)),
list("solver" = "hybrid", "solver.control" = list()),
list("solver" = "nloptr", "solver.control" = list("solver" = 1)), # COBYLA
list("solver" = "nloptr", "solver.control" = list("solver" = 2)), # BOBYQA
list("solver" = "nloptr", "solver.control" = list("solver" = 3)), # PRAXIS
list("solver" = "nloptr",
"solver.control" = list("solver" = 4)), # NELDERMEAD
list("solver" = "nloptr", "solver.control" = list("solver" = 5)), # SBPLX
list("solver" = "nloptr",
"solver.control" = list("solver" = 6)), # AUGLAG+COBYLA
list("solver" = "nloptr",
"solver.control" = list("solver" = 7)), # AUGLAG+BOBYQA
list("solver" = "nloptr",
"solver.control" = list("solver" = 8)), # AUGLAG+PRAXIS
list("solver" = "nloptr",
"solver.control" = list("solver" = 9)), # AUGLAG+NELDERMEAD
list("solver" = "nloptr",
"solver.control" = list("solver" = 10)) # AUGLAG+SBPLX
)
tags <- c(
# Names for the above list
"nlminb",
"solnp",
"lbfgs",
"gosolnp",
"hybrid",
"nloptr+COBYLA",
"nloptr+BOBYQA",
"nloptr+PRAXIS",
"nloptr+NELDERMEAD",
"nloptr+SBPLX",
"nloptr+AUGLAG+COBYLA",
"nloptr+AUGLAG+BOBYQA",
"nloptr+AUGLAG+PRAXIS",
"nloptr+AUGLAG+NELDERMEAD",
"nloptr+AUGLAG+SBPLX"
)
names(solvers) <- tags現在讓我們進行優化計算選擇的交叉射擊(gauntlet),看看哪個演算法產生的估計在模型 1 生成的數據上達到最大的對數似然。遺憾的是,lbfgs 方法(Broyden-Fletcher-Goldfarb-Shanno 方法的低存儲版本)在這個序列上沒有收斂,所以我省略了它。
optMethodCompare <- function(data,
spec,
solvers)
{
# Runs all solvers in a list for a dataset
#
# Args:
# data: An object to pass to ugarchfit's data parameter containing the data
# to fit
# spec: A specification created by ugarchspec to pass to ugarchfit
# solvers: A list of lists containing strings of solvers and a list for
# solver.control
#
# Return:
# A matrix containing the result of the solvers (including parameters, se's,
# and LLH)
model_solutions <- lapply(
solvers,
function(s)
{
args <- s
args[["spec"]] <- spec
args[["data"]] <- data
res <- do.call(evalSolverFit, args = args)
return(res)
})
model_solutions <- do.call(
rbind, model_solutions)
return(model_solutions)
}
round(
optMethodCompare(
x1, spec, solvers[c(1:2, 4:15)]), digits = 4)## omega alpha1 beta1 se.omega se.alpha1 se.beta1 robust.se.omega robust.se.alpha1 robust.se.beta1 LLH
## ------------------------- ------- ------- ------- --------- ---------- --------- ---------------- ----------------- ---------------- ----------
## nlminb 0.2689 0.1774 0.0000 0.0787 0.0472 0.2447 0.0890 0.0352 0.2830 -849.6927
## solnp 0.0007 0.0029 0.9947 0.0013 0.0037 0.0004 0.0012 0.0037 0.0001 -860.4860
## gosolnp 0.2689 0.1774 0.0000 0.0787 0.0472 0.2446 0.0890 0.0352 0.2828 -849.6927
## hybrid 0.0007 0.0029 0.9947 0.0013 0.0037 0.0004 0.0012 0.0037 0.0001 -860.4860
## nloptr+COBYLA 0.0006 0.0899 0.9101 0.0039 0.0306 0.0370 0.0052 0.0527 0.0677 -871.5006
## nloptr+BOBYQA 0.0003 0.0907 0.9093 0.0040 0.0298 0.0375 0.0057 0.0532 0.0718 -872.3436
## nloptr+PRAXIS 0.2689 0.1774 0.0000 0.0786 0.0472 0.2444 0.0888 0.0352 0.2823 -849.6927
## nloptr+NELDERMEAD 0.0010 0.0033 0.9935 0.0013 0.0039 0.0004 0.0013 0.0038 0.0001 -860.4845
## nloptr+SBPLX 0.0010 0.1000 0.9000 0.0042 0.0324 0.0386 0.0055 0.0536 0.0680 -872.2736
## nloptr+AUGLAG+COBYLA 0.0006 0.0899 0.9101 0.0039 0.0306 0.0370 0.0052 0.0527 0.0677 -871.5006
## nloptr+AUGLAG+BOBYQA 0.0003 0.0907 0.9093 0.0040 0.0298 0.0375 0.0057 0.0532 0.0718 -872.3412
## nloptr+AUGLAG+PRAXIS 0.1246 0.1232 0.4948 0.0620 0.0475 0.2225 0.0701 0.0439 0.2508 -851.0547
## nloptr+AUGLAG+NELDERMEAD 0.2689 0.1774 0.0000 0.0786 0.0472 0.2445 0.0889 0.0352 0.2826 -849.6927
## nloptr+AUGLAG+SBPLX 0.0010 0.1000 0.9000 0.0042 0.0324 0.0386 0.0055 0.0536 0.0680 -872.2736根據最大似然準則,“最優”結果是由 gosolnp 實現的。結果有一個不幸的屬性——\(\beta \approx 0\),這當然不是正確的,但至少 \(\beta\) 的標準差會創建一個包含 \(\beta\) 真值的置信區間。其中,我的首選估計是由 AUGLAG + PRAXIS 生成的,因為 \(\beta\) 似乎是合理的,事實上估計都接近事實(至少在置信區間包含真值的意義上),但不幸的是,即使它們是最合理的,估計並沒有最大化對數似然。
如果我們看一下模型 2,我們會看到什麼?同樣,lbfgs 沒有收斂,所以我省略忽略了它。不幸的是,nlminb 也沒有收斂,因此也必須省略。
round(
optMethodCompare(
x2, spec, solvers[c(2, 4:15)]), digits = 4)## omega alpha1 beta1 se.omega se.alpha1 se.beta1 robust.se.omega robust.se.alpha1 robust.se.beta1 LLH
## ------------------------- ------- ------- ------- --------- ---------- --------- ---------------- ----------------- ---------------- ----------
## solnp 0.0011 0.0020 0.9970 0.0025 0.0029 0.0005 0.0030 0.0035 0.0004 -1375.951
## gosolnp 0.0011 0.0020 0.9970 0.0025 0.0029 0.0005 0.0030 0.0035 0.0004 -1375.951
## hybrid 0.0011 0.0020 0.9970 0.0025 0.0029 0.0005 0.0030 0.0035 0.0004 -1375.951
## nloptr+COBYLA 0.0016 0.0888 0.9112 0.0175 0.0619 0.0790 0.0540 0.2167 0.2834 -1394.529
## nloptr+BOBYQA 0.0010 0.0892 0.9108 0.0194 0.0659 0.0874 0.0710 0.2631 0.3572 -1395.310
## nloptr+PRAXIS 0.5018 0.0739 0.3803 0.3178 0.0401 0.3637 0.2777 0.0341 0.3225 -1373.632
## nloptr+NELDERMEAD 0.0028 0.0026 0.9944 0.0028 0.0031 0.0004 0.0031 0.0035 0.0001 -1375.976
## nloptr+SBPLX 0.0029 0.1000 0.9000 0.0146 0.0475 0.0577 0.0275 0.1108 0.1408 -1395.807
## nloptr+AUGLAG+COBYLA 0.0016 0.0888 0.9112 0.0175 0.0619 0.0790 0.0540 0.2167 0.2834 -1394.529
## nloptr+AUGLAG+BOBYQA 0.0010 0.0892 0.9108 0.0194 0.0659 0.0874 0.0710 0.2631 0.3572 -1395.310
## nloptr+AUGLAG+PRAXIS 0.5018 0.0739 0.3803 0.3178 0.0401 0.3637 0.2777 0.0341 0.3225 -1373.632
## nloptr+AUGLAG+NELDERMEAD 0.0001 0.0000 1.0000 0.0003 0.0003 0.0000 0.0004 0.0004 0.0000 -1375.885
## nloptr+AUGLAG+SBPLX 0.0029 0.1000 0.9000 0.0146 0.0475 0.0577 0.0275 0.1108 0.1408 -1395.807這裡是 PRAXIS 和 AUGLAG + PRAXIS 給出了“最優”結果,只有這兩種方法做到了。其他優化器給出了明顯糟糕的結果。也就是說,“最優”解在參數為非零、置信區間包含正確值上是首選的。
如果我們將樣本限製為 100,會發生什麼?(lbfgs 仍然不起作用。)
round(
optMethodCompare(
x1[1:100], spec, solvers[c(1:2, 4:15)]), digits = 4)## omega alpha1 beta1 se.omega se.alpha1 se.beta1 robust.se.omega robust.se.alpha1 robust.se.beta1 LLH
## ------------------------- ------- ------- ------- --------- ---------- --------- ---------------- ----------------- ---------------- ---------
## nlminb 0.0451 0.2742 0.5921 0.0280 0.1229 0.1296 0.0191 0.0905 0.0667 -80.6587
## solnp 0.0451 0.2742 0.5921 0.0280 0.1229 0.1296 0.0191 0.0905 0.0667 -80.6587
## gosolnp 0.0451 0.2742 0.5921 0.0280 0.1229 0.1296 0.0191 0.0905 0.0667 -80.6587
## hybrid 0.0451 0.2742 0.5921 0.0280 0.1229 0.1296 0.0191 0.0905 0.0667 -80.6587
## nloptr+COBYLA 0.0007 0.1202 0.8798 0.0085 0.0999 0.0983 0.0081 0.1875 0.1778 -85.3121
## nloptr+BOBYQA 0.0005 0.1190 0.8810 0.0085 0.0994 0.0992 0.0084 0.1892 0.1831 -85.3717
## nloptr+PRAXIS 0.0451 0.2742 0.5921 0.0280 0.1229 0.1296 0.0191 0.0905 0.0667 -80.6587
## nloptr+NELDERMEAD 0.0451 0.2742 0.5920 0.0281 0.1230 0.1297 0.0191 0.0906 0.0667 -80.6587
## nloptr+SBPLX 0.0433 0.2740 0.5998 0.0269 0.1237 0.1268 0.0182 0.0916 0.0648 -80.6616
## nloptr+AUGLAG+COBYLA 0.0007 0.1202 0.8798 0.0085 0.0999 0.0983 0.0081 0.1875 0.1778 -85.3121
## nloptr+AUGLAG+BOBYQA 0.0005 0.1190 0.8810 0.0085 0.0994 0.0992 0.0084 0.1892 0.1831 -85.3717
## nloptr+AUGLAG+PRAXIS 0.0451 0.2742 0.5921 0.0280 0.1229 0.1296 0.0191 0.0905 0.0667 -80.6587
## nloptr+AUGLAG+NELDERMEAD 0.0451 0.2742 0.5921 0.0280 0.1229 0.1296 0.0191 0.0905 0.0667 -80.6587
## nloptr+AUGLAG+SBPLX 0.0450 0.2742 0.5924 0.0280 0.1230 0.1295 0.0191 0.0906 0.0666 -80.6587round(
optMethodCompare(
x2[1:100], spec, solvers[c(1:2, 4:15)]), digits = 4)## omega alpha1 beta1 se.omega se.alpha1 se.beta1 robust.se.omega robust.se.alpha1 robust.se.beta1 LLH
## ------------------------- ------- ------- ------- --------- ---------- --------- ---------------- ----------------- ---------------- ----------
## nlminb 0.7592 0.0850 0.0000 2.1366 0.4813 3.0945 7.5439 1.7763 11.0570 -132.4614
## solnp 0.0008 0.0000 0.9990 0.0291 0.0417 0.0066 0.0232 0.0328 0.0034 -132.9182
## gosolnp 0.0537 0.0000 0.9369 0.0521 0.0087 0.0713 0.0430 0.0012 0.0529 -132.9124
## hybrid 0.0008 0.0000 0.9990 0.0291 0.0417 0.0066 0.0232 0.0328 0.0034 -132.9182
## nloptr+COBYLA 0.0014 0.0899 0.9101 0.0259 0.0330 0.1192 0.0709 0.0943 0.1344 -135.7495
## nloptr+BOBYQA 0.0008 0.0905 0.9095 0.0220 0.0051 0.1145 0.0687 0.0907 0.1261 -135.8228
## nloptr+PRAXIS 0.0602 0.0000 0.9293 0.0522 0.0088 0.0773 0.0462 0.0015 0.0565 -132.9125
## nloptr+NELDERMEAD 0.0024 0.0000 0.9971 0.0473 0.0629 0.0116 0.0499 0.0680 0.0066 -132.9186
## nloptr+SBPLX 0.0027 0.1000 0.9000 0.0238 0.0493 0.1308 0.0769 0.1049 0.1535 -135.9175
## nloptr+AUGLAG+COBYLA 0.0014 0.0899 0.9101 0.0259 0.0330 0.1192 0.0709 0.0943 0.1344 -135.7495
## nloptr+AUGLAG+BOBYQA 0.0008 0.0905 0.9095 0.0221 0.0053 0.1145 0.0687 0.0907 0.1262 -135.8226
## nloptr+AUGLAG+PRAXIS 0.0602 0.0000 0.9294 0.0523 0.0090 0.0771 0.0462 0.0014 0.0565 -132.9125
## nloptr+AUGLAG+NELDERMEAD 0.0000 0.0000 0.9999 0.0027 0.0006 0.0005 0.0013 0.0004 0.0003 -132.9180
## nloptr+AUGLAG+SBPLX 0.0027 0.1000 0.9000 0.0238 0.0493 0.1308 0.0769 0.1049 0.1535 -135.9175結果並不令人興奮。多個求解器獲得了模型 1 生成序列的“最佳”結果,同時 \(\omega\) 的 95% 置信區間(CI)不包含 \(\omega\) 的真實值,儘管其他的 CI 將包含其真實值。對於由模型 2 生成的序列,最佳結果是由 nlminb 求解器實現的,但參數值不合理,標準差很大。至少 CI 將包含正確值。
從這裡開始,我們不應再僅僅關註兩個序列,而是在兩個模型生成的許多模擬序列中研究這些方法的表現。這篇文章中的模擬對於我的筆記本電腦而言計算量太大,因此我將使用我院系的超級電腦來執行它們,利用其多核進行並行計算。
library(foreach)
library(doParallel)
logfile <- ""
# logfile <- "outfile.log"
# if (!file.exists(logfile)) {
# file.create(logfile)
# }
cl <- makeCluster(
detectCores() - 1, outfile = logfile)
registerDoParallel(cl)
optMethodSims <- function(
gen_spec,
n.sim = 1000,
m.sim = 1000,
fit_spec = ugarchspec(
mean.model = list(
armaOrder = c(0,0), include.mean = FALSE)),
solvers = list(
"solnp" = list(
"solver" = "solnp", "solver.control" = list())),
rseed = NA, verbose = FALSE)
{
# Performs simulations in parallel of GARCH processes via rugarch and returns
# a list with the results of different optimization routines
#
# Args:
# gen_spec: The specification for generating a GARCH sequence, produced by
# ugarchspec
# n.sim: An integer denoting the length of the simulated series
# m.sim: An integer for the number of simulated sequences to generate
# fit_spec: A ugarchspec specification for the model to fit
# solvers: A list of lists containing strings of solvers and a list for
# solver.control
# rseed: Optional seeding value(s) for the random number generator. For
# m.sim>1, it is possible to provide either a single seed to
# initialize all values, or one seed per separate simulation (i.e.
# m.sim seeds). However, in the latter case this may result in some
# slight overhead depending on how large m.sim is
# verbose: Boolean for whether to write data tracking the progress of the
# loop into an output file
# outfile: A string for the file to store verbose output to (relevant only
# if verbose is TRUE)
#
# Return:
# A list containing the result of calling optMethodCompare on each generated
# sequence
fits <- foreach(
i = 1:m.sim,
.packages = c("rugarch"),
.export = c(
"optMethodCompare", "evalSolverFit")) %dopar%
{
if (is.na(rseed))
{
newseed <- NA
}
else if (is.vector(rseed))
{
newseed <- rseed[i]
}
else
{
newseed <- rseed + i - 1
}
if (verbose)
{
cat(as.character(Sys.time()), ": Now on simulation ", i, "\n")
}
sim <- ugarchpath(
gen_spec, n.sim = n.sim, n.start = 1000,
m.sim = 1, rseed = newseed)
x <- sim@path$seriesSim
optMethodCompare(
x, spec = fit_spec, solvers = solvers)
}
return(fits)
}
# Specification 1 first
spec1_n100 <- optMethodSims(
spec1, n.sim = 100, m.sim = 1000,
solvers = solvers, verbose = TRUE)
spec1_n500 <- optMethodSims(
spec1, n.sim = 500, m.sim = 1000,
solvers = solvers, verbose = TRUE)
spec1_n1000 <- optMethodSims(
spec1, n.sim = 1000, m.sim = 1000,
solvers = solvers, verbose = TRUE)
# Specification 2 next
spec2_n100 <- optMethodSims(
spec2, n.sim = 100, m.sim = 1000,
solvers = solvers, verbose = TRUE)
spec2_n500 <- optMethodSims(
spec2, n.sim = 500, m.sim = 1000,
solvers = solvers, verbose = TRUE)
spec2_n1000 <- optMethodSims(
spec2, n.sim = 1000, m.sim = 1000,
solvers = solvers, verbose = TRUE)以下是一組輔助函數,用於我要進行的分析。
optMethodSims_getAllVals <- function(param,
solver,
reslist)
{
# Get all values for a parameter obtained by a certain solver after getting a
# list of results via optMethodSims
#
# Args:
# param: A string for the parameter to get (such as "beta1")
# solver: A string for the solver for which to get the parameter (such as
# "nlminb")
# reslist: A list created by optMethodSims
#
# Return:
# A vector of values of the parameter for each simulation
res <- sapply(
reslist,
function(l)
{
return(l[solver, param])
})
return(res)
}
optMethodSims_getBestVals <- function(reslist,
opt_vec = TRUE,
reslike = FALSE)
{
# A function that gets the optimizer that maximized the likelihood function
# for each entry in reslist
#
# Args:
# reslist: A list created by optMethodSims
# opt_vec: A boolean indicating whether to return a vector with the name of
# the optimizers that maximized the log likelihood
# reslike: A bookean indicating whether the resulting list should consist of
# matrices of only one row labeled "best" with a structure like
# reslist
#
# Return:
# If opt_vec is TRUE, a list of lists, where each sublist contains a vector
# of strings naming the opimizers that maximized the likelihood function and
# a matrix of the parameters found. Otherwise, just the matrix (resembles
# the list generated by optMethodSims)
res <- lapply(
reslist,
function(l)
{
max_llh <- max(l[, "LLH"], na.rm = TRUE)
best_idx <- (l[, "LLH"] == max_llh) & (!is.na(l[, "LLH"]))
best_mat <- l[best_idx, , drop = FALSE]
if (opt_vec)
{
return(
list(
"solvers" = rownames(best_mat), "params" = best_mat))
}
else
{
return(best_mat)
}
})
if (reslike)
{
res <- lapply(
res,
function(l)
{
mat <- l$params[1, , drop = FALSE]
rownames(mat) <- "best"
return(mat)
})
}
return(res)
}
optMethodSims_getCaptureRate <- function(param,
solver,
reslist,
multiplier = 2,
spec,
use_robust = TRUE)
{
# Gets the rate a confidence interval for a parameter captures the true value
#
# Args:
# param: A string for the parameter being worked with
# solver: A string for the solver used to estimate the parameter
# reslist: A list created by optMethodSims
# multiplier: A floating-point number for the multiplier to the standard
# error, appropriate for the desired confidence level
# spec: A ugarchspec specification with the fixed parameters containing the
# true parameter value
# use_robust: Use robust standard errors for computing CIs
#
# Return:
# A float for the proportion of times the confidence interval captured the
# true parameter value
se_string <- ifelse(
use_robust, "robust.se.", "se.")
est <- optMethodSims_getAllVals(
param, solver, reslist)
moe_est <- multiplier * optMethodSims_getAllVals(
paste0(se_string, param), solver, reslist)
param_val <- spec@model$fixed.pars[[param]]
contained <- (param_val <= est + moe_est) & (param_val >= est - moe_est)
return(mean(contained, na.rm = TRUE))
}
optMethodSims_getMaxRate <- function(solver,
maxlist)
{
# Gets how frequently a solver found a maximal log likelihood
#
# Args:
# solver: A string for the solver
# maxlist A list created by optMethodSims_getBestVals with entries
# containing vectors naming the solvers that maximized the log
# likelihood
#
# Return:
# The proportion of times the solver maximized the log likelihood
maxed <- sapply(
maxlist,
function(l)
{
solver %in% l$solvers
})
return(mean(maxed))
}
optMethodSims_getFailureRate <- function(solver,
reslist)
{
# Computes the proportion of times a solver failed to converge.
#
# Args:
# solver: A string for the solver
# reslist: A list created by optMethodSims
#
# Return:
# Numeric proportion of times a solver failed to converge
failed <- sapply(
reslist,
function(l)
{
is.na(l[solver, "LLH"])
})
return(mean(failed))
}
# Vectorization
optMethodSims_getCaptureRate <- Vectorize(
optMethodSims_getCaptureRate, vectorize.args = "solver")
optMethodSims_getMaxRate <- Vectorize(
optMethodSims_getMaxRate, vectorize.args = "solver")
optMethodSims_getFailureRate <- Vectorize(
optMethodSims_getFailureRate, vectorize.args = "solver")我首先為固定樣本量和模型創建表:
- 所有求解器中,某個求解器達到最高對數似然的頻率
- 某個求解器未能收斂的頻率
- 基於某個求解器的解,95% 置信區間包含每個參數真實值的頻率(稱為“捕獲率”,並使用穩健標準差)
solver_table <- function(reslist,
tags,
spec)
{
# Creates a table describing important solver statistics
#
# Args:
# reslist: A list created by optMethodSims
# tags: A vector with strings naming all solvers to include in the table
# spec: A ugarchspec specification with the fixed parameters containing the
# true parameter value
#
# Return:
# A matrix containing metrics describing the performance of the solvers
params <- names(spec1@model$fixed.pars)
max_rate <- optMethodSims_getMaxRate(
tags, optMethodSims_getBestVals(reslist))
failure_rate <- optMethodSims_getFailureRate(
tags, reslist)
capture_rate <- lapply(
params,
function(p)
{
optMethodSims_getCaptureRate(
p, tags, reslist, spec = spec)
})
return_mat <- cbind(
"Maximization Rate" = max_rate,
"Failure Rate" = failure_rate)
capture_mat <- do.call(cbind, capture_rate)
colnames(capture_mat) <- paste(
params, "95% CI Capture Rate")
return_mat <- cbind(
return_mat, capture_mat)
return(return_mat)
}- Model 1, \(n=100\)
as.data.frame(
round(
solver_table(spec1_n100, tags, spec1) * 100,
digits = 1))## Maximization Rate Failure Rate omega 95% CI Capture Rate alpha1 95% CI Capture Rate beta1 95% CI Capture Rate
## ------------------------- ------------------ ------------- -------------------------- --------------------------- --------------------------
## nlminb 16.2 20.0 21.8 29.2 24.0
## solnp 0.1 0.0 13.7 24.0 15.4
## lbfgs 15.1 35.2 56.6 67.9 58.0
## gosolnp 20.3 0.0 20.3 32.6 21.9
## hybrid 0.1 0.0 13.7 24.0 15.4
## nloptr+COBYLA 0.0 0.0 6.3 82.6 19.8
## nloptr+BOBYQA 0.0 0.0 5.4 82.1 18.5
## nloptr+PRAXIS 15.8 0.0 42.1 54.5 44.1
## nloptr+NELDERMEAD 0.4 0.0 5.7 19.3 8.1
## nloptr+SBPLX 0.1 0.0 7.7 85.7 24.1
## nloptr+AUGLAG+COBYLA 0.0 0.0 6.1 84.5 19.9
## nloptr+AUGLAG+BOBYQA 0.1 0.0 6.5 83.2 19.4
## nloptr+AUGLAG+PRAXIS 22.6 0.0 41.2 54.6 44.1
## nloptr+AUGLAG+NELDERMEAD 11.1 0.0 7.5 18.8 9.7
## nloptr+AUGLAG+SBPLX 0.6 0.0 7.9 86.5 23.0- Model 1, \(n=500\)
as.data.frame(
round(
solver_table(spec1_n500, tags, spec1) * 100,
digits = 1))## Maximization Rate Failure Rate omega 95% CI Capture Rate alpha1 95% CI Capture Rate beta1 95% CI Capture Rate
## ------------------------- ------------------ ------------- -------------------------- --------------------------- --------------------------
## nlminb 21.2 0.4 63.3 67.2 63.8
## solnp 0.1 0.2 32.2 35.6 32.7
## lbfgs 4.5 41.3 85.0 87.6 85.7
## gosolnp 35.1 0.0 69.0 73.2 69.5
## hybrid 0.1 0.0 32.3 35.7 32.8
## nloptr+COBYLA 0.0 0.0 3.2 83.3 17.8
## nloptr+BOBYQA 0.0 0.0 3.5 81.5 18.1
## nloptr+PRAXIS 18.0 0.0 83.9 87.0 84.2
## nloptr+NELDERMEAD 0.0 0.0 16.4 20.7 16.7
## nloptr+SBPLX 0.1 0.0 3.7 91.4 15.7
## nloptr+AUGLAG+COBYLA 0.0 0.0 3.2 83.3 17.8
## nloptr+AUGLAG+BOBYQA 0.0 0.0 3.5 81.5 18.1
## nloptr+AUGLAG+PRAXIS 21.9 0.0 80.2 87.4 83.4
## nloptr+AUGLAG+NELDERMEAD 0.6 0.0 20.0 24.0 20.5
## nloptr+AUGLAG+SBPLX 0.0 0.0 3.7 91.4 15.7- Model 1, \(n=1000\)
as.data.frame(
round(
solver_table(spec1_n1000, tags, spec1) * 100,
digits = 1))## Maximization Rate Failure Rate omega 95% CI Capture Rate alpha1 95% CI Capture Rate beta1 95% CI Capture Rate
## ------------------------- ------------------ ------------- -------------------------- --------------------------- --------------------------
## nlminb 21.5 0.1 88.2 86.1 87.8
## solnp 0.4 0.2 54.9 53.6 54.6
## lbfgs 1.1 44.8 91.5 88.0 91.8
## gosolnp 46.8 0.0 87.2 85.1 87.0
## hybrid 0.5 0.0 55.0 53.6 54.7
## nloptr+COBYLA 0.0 0.0 4.1 74.5 15.0
## nloptr+BOBYQA 0.0 0.0 3.6 74.3 15.9
## nloptr+PRAXIS 17.7 0.0 92.6 90.2 92.2
## nloptr+NELDERMEAD 0.0 0.0 30.5 29.6 30.9
## nloptr+SBPLX 0.0 0.0 3.0 82.3 11.6
## nloptr+AUGLAG+COBYLA 0.0 0.0 4.1 74.5 15.0
## nloptr+AUGLAG+BOBYQA 0.0 0.0 3.6 74.3 15.9
## nloptr+AUGLAG+PRAXIS 13.0 0.0 83.4 93.9 86.7
## nloptr+AUGLAG+NELDERMEAD 0.0 0.0 34.6 33.8 35.0
## nloptr+AUGLAG+SBPLX 0.0 0.0 3.0 82.3 11.6- Model 2, \(n=100\)
as.data.frame(
round(
solver_table(spec2_n100, tags, spec2) * 100,
digits = 1))## Maximization Rate Failure Rate omega 95% CI Capture Rate alpha1 95% CI Capture Rate beta1 95% CI Capture Rate
## ------------------------- ------------------ ------------- -------------------------- --------------------------- --------------------------
## nlminb 8.2 24.2 22.3 34.7 23.9
## solnp 0.3 0.0 21.1 32.6 21.3
## lbfgs 11.6 29.5 74.9 73.2 70.4
## gosolnp 19.0 0.0 31.9 41.2 30.8
## hybrid 0.3 0.0 21.1 32.6 21.3
## nloptr+COBYLA 0.0 0.0 20.5 94.7 61.7
## nloptr+BOBYQA 0.2 0.0 19.3 95.8 62.2
## nloptr+PRAXIS 16.0 0.0 70.2 57.2 52.8
## nloptr+NELDERMEAD 0.2 0.0 7.8 27.8 14.1
## nloptr+SBPLX 0.1 0.0 24.9 91.0 65.0
## nloptr+AUGLAG+COBYLA 0.0 0.0 21.2 95.1 62.5
## nloptr+AUGLAG+BOBYQA 0.9 0.0 20.1 96.2 62.5
## nloptr+AUGLAG+PRAXIS 38.8 0.0 70.4 57.2 52.7
## nloptr+AUGLAG+NELDERMEAD 14.4 0.0 10.7 26.0 16.1
## nloptr+AUGLAG+SBPLX 0.1 0.0 25.8 91.9 65.5- Model 2, \(n=500\)
as.data.frame(
round(
solver_table(spec2_n500, tags, spec2) * 100,
digits = 1))## Maximization Rate Failure Rate omega 95% CI Capture Rate alpha1 95% CI Capture Rate beta1 95% CI Capture Rate
## ------------------------- ------------------ ------------- -------------------------- --------------------------- --------------------------
## nlminb 1.7 1.6 35.0 37.2 34.2
## solnp 0.1 0.2 46.2 48.6 45.3
## lbfgs 2.2 38.4 85.2 88.1 82.3
## gosolnp 5.2 0.0 74.9 77.8 72.7
## hybrid 0.1 0.0 46.1 48.5 45.2
## nloptr+COBYLA 0.0 0.0 8.2 100.0 40.5
## nloptr+BOBYQA 0.0 0.0 9.5 100.0 41.0
## nloptr+PRAXIS 17.0 0.0 83.8 85.1 81.0
## nloptr+NELDERMEAD 0.0 0.0 26.9 38.2 27.0
## nloptr+SBPLX 0.0 0.0


