Python語言程式設計之二--用turtle庫畫圍棋棋盤和正、餘弦函數圖形

這篇筆記依然是在做《Python語言程式設計》第5章迴圈的習題。其中有兩類問題需要記錄下來。

第一是如何畫圍棋棋盤。圍棋棋盤共有19縱19橫。其中，位於（0，0）的星位叫天元，其餘8個星位坐標分別是：（-6，6），（0，6），（6，6），（-6，0），（6，0），（-6，-6），（0，-6），（6，-6）。這裡面涉及到繪製等間距網格，我選擇for迴圈來實現。考慮到以後可以修改棋盤大小，所以網格間距和初始點位置都設置成全局變數。其代碼如下：

# 繪製圍棋棋盤

import turtle

# 線與線間隔
n = 30
# 初始點位置
x = -300
y = -300

# 定義棋盤樣式
turtle.speed(3)
turtle.pencolor('black')
turtle.screensize(400, 400)

# 畫橫線
for i in range(19):
    turtle.penup()
    turtle.goto(x, y + n * i)
    turtle.pendown()
    turtle.forward(n * 18)

# 畫豎線
turtle.left(90)
for i in range(19):
    turtle.penup()
    turtle.goto(x + n * i, y)
    turtle.pendown()
    turtle.forward(n * 18)

turtle.right(90)

# 畫9個星位，每排三個，共三排所以是兩層for迴圈
x_first = x + n * 3
y_first = y + n * 3 - n * 0.25

for i in range(3):
    for j in range(3):
        turtle.penup()
        turtle.goto(x_first + 6 * j * n, y_first + 6 * i * n)
        # 如果按下麵寫法，則先畫左邊3個星，再畫中間3個
        # turtle.goto(x_first + 6 * j * n, y_first + 6 * i * n)
        turtle.pendown()
        turtle.begin_fill()
        turtle.fillcolor('blue')
        # 飛星的半徑為1/4個網格間距
        turtle.circle(n * 0.25)
        turtle.end_fill()

# 隱藏畫筆箭頭
turtle.hideturtle()

turtle.done()

代碼運行結果如下圖：

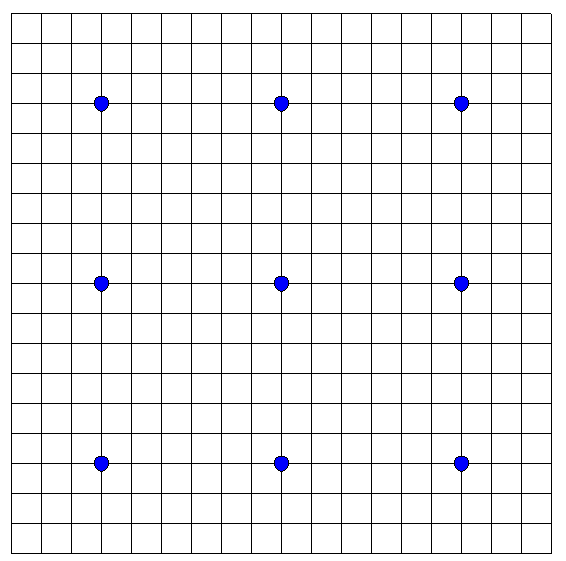
題目非常簡單，重點是通過畫圖來感受迴圈在處理重覆性動作時的威力。但凡重覆性的工作都可以用迴圈來處理。這也正是電腦擅長的工作，並且也是程式的意義所在：把人的精力從繁瑣的、海量的、重覆性的、簡單的初級工作中解脫出來。

第二個問題就是繪製正弦、餘弦函數。其核心思想是：放下畫筆，然後讓畫筆依次通過各個坐標點就畫出一條正弦餘弦曲線。從這裡也可以看出，這也是不斷地重覆性工作，重覆地計算以x為橫坐標的點的 y 坐標，然後重覆地讓畫筆通過這些點。所以我也選用for迴圈。

當然，代碼中值得關註的就是 x-0-y 坐標系的繪製。這段代碼可以通用。

# 在正交坐標系下畫sin(x)和cos(x)曲線

import turtle
import math

turtle.speed(1)

# 畫 x 軸
turtle.penup()
turtle.goto(-220, 0)
turtle.pendown()
turtle.goto(220, 0)

# 畫 x 軸箭頭
turtle.setheading(150)
turtle.forward(20)
turtle.penup()
turtle.goto(220, 0)
turtle.setheading(-150)
turtle.pendown()
turtle.forward(20)

# 顯示x
turtle.penup()
turtle.goto(225, 0)
turtle.write('X')

# 畫 y 軸
turtle.penup()
turtle.goto(0, -100)
turtle.pendown()
turtle.goto(0, 100)

# 畫 y 軸箭頭
turtle.setheading(240)
turtle.forward(20)
turtle.penup()
turtle.goto(0, 100)
turtle.pendown()
turtle.setheading(-60)
turtle.forward(20)

# 顯示Y
turtle.penup()
turtle.goto(0, 110)
turtle.write('Y')

# 畫正弦曲線
x = -175
turtle.pensize(2)
turtle.color('blue')
turtle.penup()
turtle.goto(x, 50 * math.sin((x / 100) * 2 * math.pi))
turtle.pendown()
for x in range(-175, 176):
    turtle.goto(x, 50 * math.sin((x / 100) * 2 * math.pi))

# 將-2π的位置標示出來
turtle.penup()
turtle.goto(-100, -20)
turtle.write('-2π')

# 將2π的位置標示出來
turtle.penup()
turtle.goto(100, -20)
turtle.write('2π')

# 畫餘弦曲線
x = -175
turtle.pensize(2)
turtle.color('red')
turtle.penup()
turtle.goto(x, 50 * math.cos((x / 100) * 2 * math.pi))
turtle.pendown()
for x in range(-175, 176):
    turtle.goto(x, 50 * math.cos((x / 100) * 2 * math.pi))

turtle.hideturtle()
turtle.done()

運行結果如下：

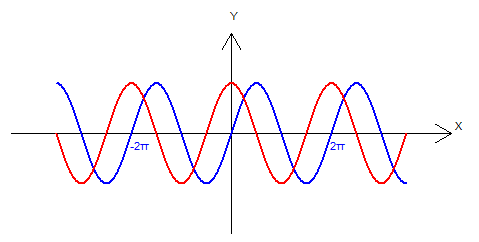
最後我還是要重覆一遍上面的心得：但凡重覆性的工作都可以用迴圈來處理。這也正是電腦擅長的工作，並且也是程式的意義所在：把人的精力從繁瑣的、海量的、重覆性的、簡單的初級工作中解脫出來。應該把精力放在建模和演算法優化上。這才是重點和難點。

這句話重覆了，可以for一下。哈哈，皮