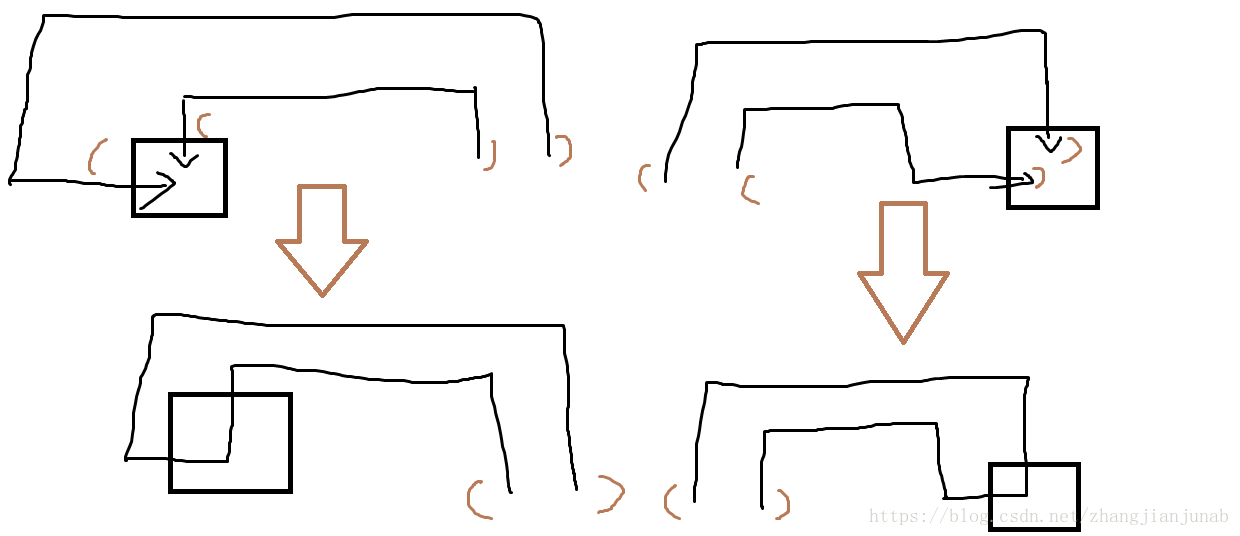今天,我,Monkey ~~king~~ 又為大家帶來大(ju)佬(ruo)的演算法啦!——插頭DP 例題(菜OJ上的網址:http://caioj.cn/problem.php?id=1489): 那麼,這道題怎麼做呢?~~(雖然菜OJ上有視頻)~~ 插頭DP能完美解決! 註:我採用的是括弧表示法~ ...
今天,我,Monkey king 又為大家帶來大(ju)佬(ruo)的演算法啦!——插頭DP
例題(菜OJ上的網址:http://caioj.cn/problem.php?id=1489):
那麼,這道題怎麼做呢?(雖然菜OJ上有視頻)
插頭DP能完美解決!
註:我採用的是括弧表示法(一個神奇的、猛如虎的神奇表示法)
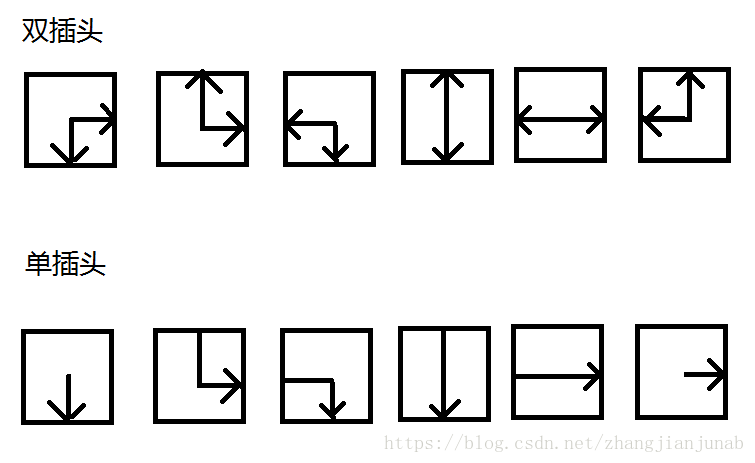
首先,我們先講一下插頭,總共6種雙插頭(一般用來解決迴路問題和輔助單插頭完成路徑問題)和不知多少種單插頭(用來解決路徑問題)
別看插頭多,其實大部分相同!
插頭:

畫得好醜
註:這隻畫了6種單插頭,因為單插頭在不同情況下可能會分(泌)出不同的情況,所以單插頭難度比較大。
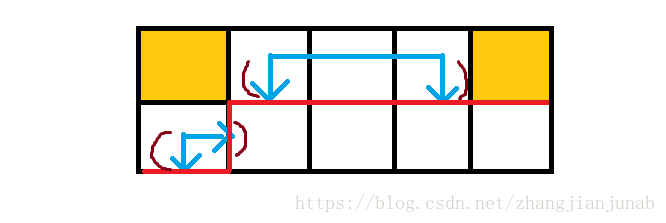
現在講一下輪廓線:
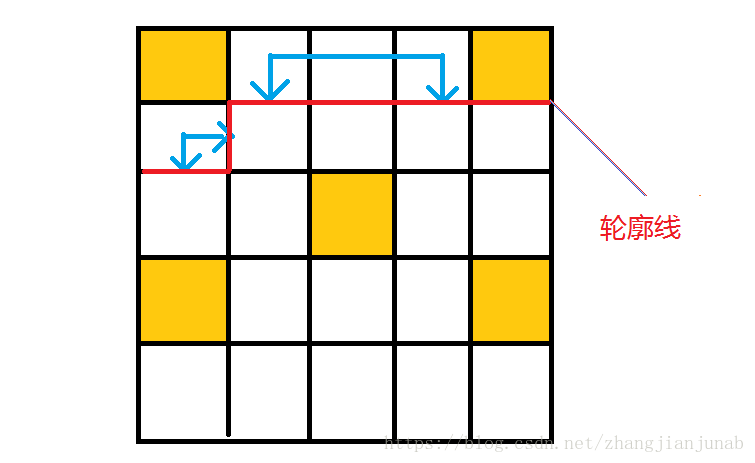
紅不溜秋的東西十分重要!
如圖,一條迴路如同一大堆插頭拼在一起!
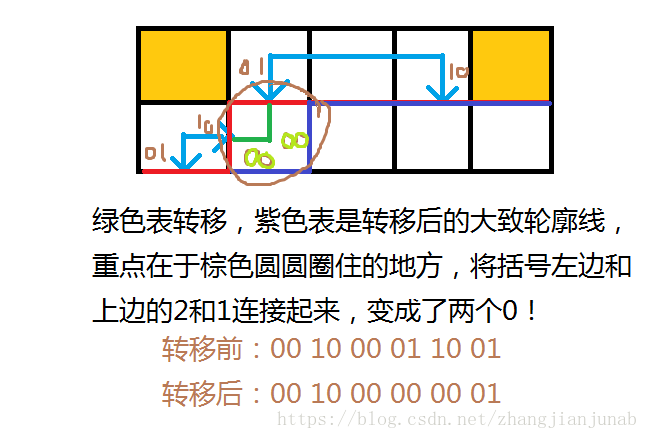
括弧表示法就是把輪廓線的狀態用括弧表示,從而壓縮狀態!
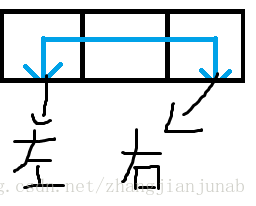
因為每一塊(連在一起的插頭)插頭左右的要去擴張的插頭會一直往下擴,所以不會出現左插頭飛右插頭右邊
如:
所以,我們可以把左插頭表示為左括弧,右插頭為右括弧(一對),插頭中的一部分或沒插頭為空。
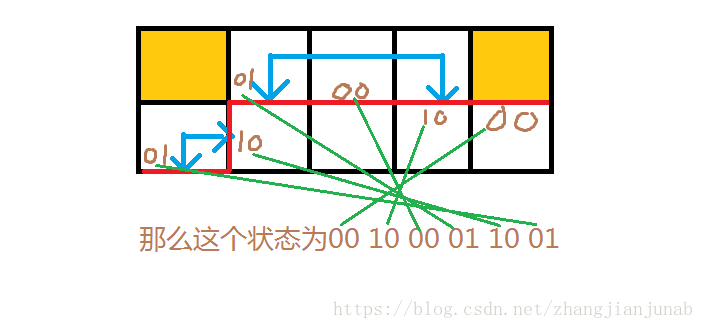
但是,狀態壓縮呀,總不可能開個字元吧!那麼,把左插頭表示成1,右插頭為2,空為0,每個數用兩個二進位表示:01,10,00
然後,從左讓右將二進位數合成一個大的數,用來表示當前狀態!
如:
因為要包括沒搞定的格子,所以輪廓線長度為m(矩陣寬度)+1
那麼為什麼要用二進位呢?位運算!
取出第輪廓線上的第q個位置的數:
int set(int s,int p)
{
return (s>>((p-1)*2))&3;
}改變第q位上的數為v:
void change(int &s/*引用,別打漏了*/,int p,int v)
{
s^=set(s,p)<<((p-1)*2);
s^=v<<((p-1)*2);
}不理解的同學搜一下C++的位運算理解一下!
其實,插頭講究的是分類討論,對每種插頭情況分類討論!
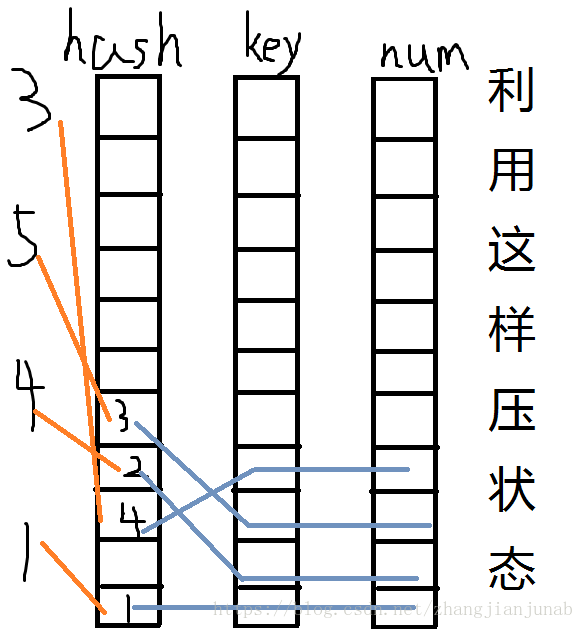
先將Hash表,定一個inf和幾個數組
定x,y,z,k分別%inf後得1 4 5 3
那麼,得:
代碼如下:
struct node
{
int hash[mod]/*壓狀態*/,key[mod]/*記錄原本的數值*/,size/*記錄存了多少數*/;ll num[mod]/*記錄當前數值代表了多少狀態*/;
void mem()
{
memset(hash,-1,sizeof(hash));size=0;//初始化函數
}
void add(int S,ll sum)
{
int s=S%mod;
while(hash[s]!=-1 && key[hash[s]]!=S)
{
s++;s%=mod;
}//判斷重覆,這樣做是可以保證下次扔一個同樣的數也可以到這個hash值
if(hash[s]==-1)
{
hash[s]=++size;key[size]=S;num[size]=sum;
}//新建一個hash格
else num[hash[s]]+=sum;//有的話直接加
}
}dp[2];//滾動數組有人會問:為什麼同樣的數值表示不用狀態的方案數是可以加在一起的呢?
因為:
不管下麵組成怎樣,他們都可以接受,所以,他們的雖然樣子不同,但狀態相同,我們就可以把他們歸為一類。
那麼,接下來最難的其實是分類討論,插頭最難的就是因為它難調且容易漏了幾種情況。
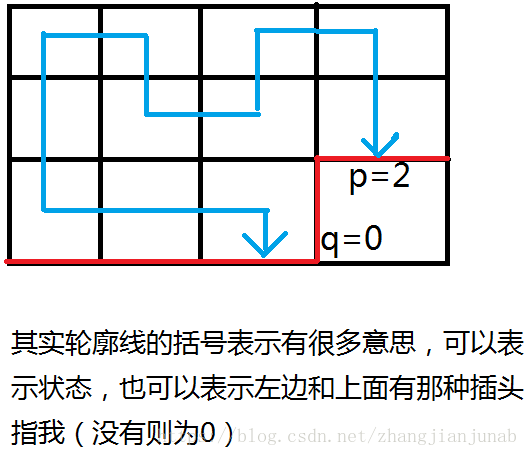
現在,我們設現在準備安上插頭的格子從左面來的插頭為q,上面來的為p。
如:
那麼,我們就要利用q和p來分類討論。。。就是代碼。。。就不要在意了(一百多行)。
現在到轉移狀態了。
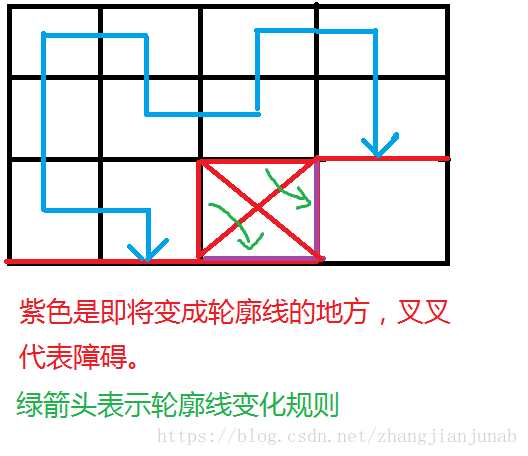
以這圖為例:
因為這是一個障礙,所以只有當q=0並且p=0可以繼承狀態。
來個沒障礙的:
那麼,再講兩種比較難想的。
這種:
插頭的概念就是可以延伸的插頭一定會去延伸或和其他插頭結合,但是什麼時候結束呢?
這道題而言:
就是當q=1並且p=2時且已經到最後一個非障礙格子時就可以將當前的狀態記入狀態。
但是!q=1並且p=2的情況不在最後一個非障礙格子時,就算一個廢的情況(提前生成迴路)。
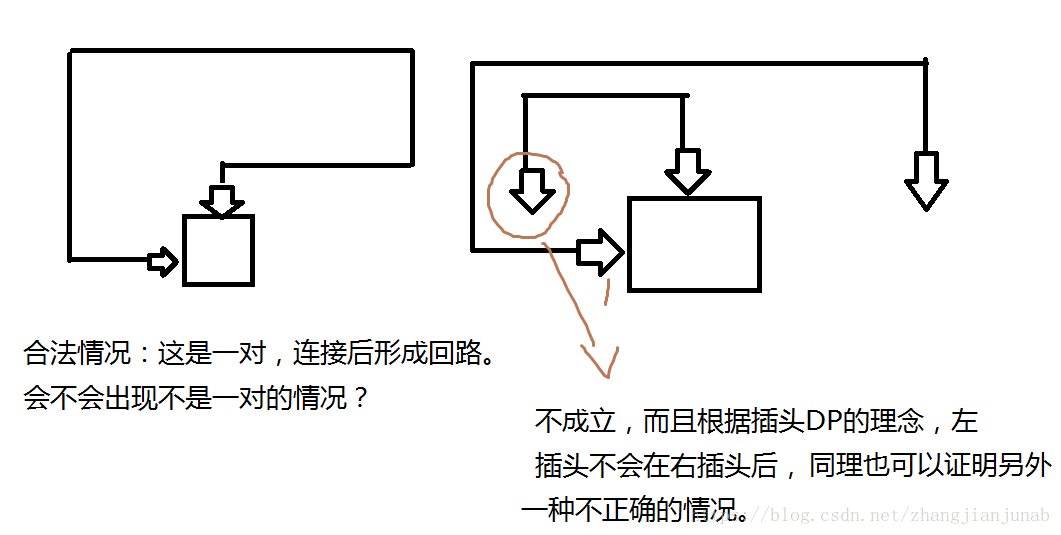
為什麼q=1並且p=2的情況一定生成迴路呢?
如圖:
那麼最後一個格會不會不會出現一對的情況?(沒有單插頭)
只要有合法情況出現,因為插頭的概念就是可以延伸的插頭一定會去延伸或和其他插頭結合,所以兩個插頭會一直延伸到最後一個格相遇!
就結束了。
註意這道題要判斷全是障礙的情況。
上代碼!
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;//不知道叫什麼,感覺很大佬,就學了^_^
const int mod=200000;//hash表大小,因為hash表有壓縮功能,所以一般100萬就夠了。
int map[50][50],n,m,ex=-1,ey=-1;//最後一個障礙格子的坐標
char ss[210];
ll ans=0;
struct node
{
int hash[mod],key[mod],size;ll num[mod];
void mem()
{
memset(hash,-1,sizeof(hash));size=0;
}//初始化
void add(int S,ll sum)
{
int s=S%mod;
while(hash[s]!=-1 && key[hash[s]]!=S)
{
s++;s%=mod;
}//找格子
if(hash[s]==-1)
{
hash[s]=++size;key[size]=S;num[size]=sum;
}
else num[hash[s]]+=sum;//將方案記錄
}
}dp[2];
int now,php;
int set(int s,int p)
{
return (s>>((p-1)*2))&3;
}//取出第k個數
void change(int &s,int p,int v)
{
s^=set(s,p)<<((p-1)*2);
s^=(v&3)<<((p-1)*2);
}//改變
void work()
{
ll sum=0;
now=0;php=1;
dp[now].mem();
dp[now].add(0,1);//初始化滾動型DP數組
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
swap(now,php);
dp[now].mem();//滾動(dan)數組
for(int k=1;k<=dp[php].size;k++)
{
int s=dp[php].key[k];
sum=dp[php].num[k];
int q=set(s,j);
int p=set(s,j+1);
if(map[i][j]==0)
{
if(q==0 && p==0)dp[now].add(s,sum);
continue;
}//障礙格子
if(q==0 && p==0)
{
if(map[i+1][j]==1 && map[i][j+1]==1)//判斷是否有障礙
{
change(s,j,1);change(s,j+1,2);//從這個格子建兩個插頭
dp[now].add(s,sum);
}
}//沒人指我,只好自己建一個插頭
else if(q>0 && p==0)
{
if(map[i+1][j]==1)dp[now].add(s,sum);//其實你拆開後簡化就是這樣子的
if(map[i][j+1]==1)//將插頭引入右邊,繼承下去
{
change(s,j,0);change(s,j+1,q);
dp[now].add(s,sum);
}
}//繼承
else if(q==0 && p>0)
{
if(map[i][j+1]==1)dp[now].add(s,sum);
if(map[i+1][j]==1)//將插頭引入下邊,繼承下去
{
change(s,j,p);change(s,j+1,0);
dp[now].add(s,sum);
}
}//繼承
else if(q==1 && p==1)
{
int find=1;//算上p為1!很重要。
for(int tt=j+2;tt<=m;tt++)//找到與p相對的右插頭並修改為這一大塊插頭的左插頭
{
int vs=set(s,tt);
if(vs==1)find++;
else if(vs==2)find--;//為什麼可以?因為中間罩住的插頭不會出去這個大插頭的範圍,所以只有碰到與p成對的插頭才會清零
if(find==0)
{
change(s,j,0);change(s,j+1,0);change(s,tt,1);
dp[now].add(s,sum);
break;//你不加這個你試試
}
}
}
else if(q==2 && p==2)
{
int find=1;
for(int tt=j-1;tt>=1;tt--)//找到與q相對的左插頭並修改為這一大塊插頭的右插頭
{
int vs=set(s,tt);
if(vs==2)find++;
else if(vs==1)find--;//這樣是不是太啰嗦了?
if(find==0)
{
change(s,j,0);change(s,j+1,0);change(s,tt,2);
dp[now].add(s,sum);
break;
}
}
}
else if(q==2 && p==1)//呵呵,這樣的狀態十分好想!因為對應的插頭剛好也是我們想要的,只要把當前的q和p連接就好了!
{
change(s,j,0);change(s,j+1,0);
dp[now].add(s,sum);
}
else if(q==1 && p==2)
{
if(ex==i && ey==j)ans+=sum;//得到答案
}
}
}
for(int j=1;j<=dp[now].size;j++)dp[now].key[j]<<=2;//看下麵解釋
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%s",ss+1);
for(int j=1;j<=m;j++)
{
if(ss[j]=='.'){map[i][j]=1;ex=i;ey=j;}//這樣做方便後面的判斷
}
}
if(ex==-1){printf("0\n");return 0;}//特判
work();
printf("%lld\n",ans);//註意答案到了long long
return 0;
}在代碼中只繼承了合法方案,不合法方案已經被過濾了
估計許多人不理解這段
else if(q==2 && p==1)
{
change(s,j,0);change(s,j+1,0);
dp[now].add(s,sum);
}如圖:
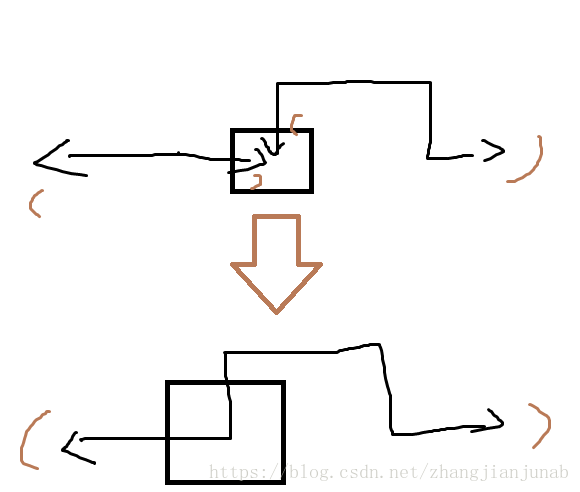
還有這段
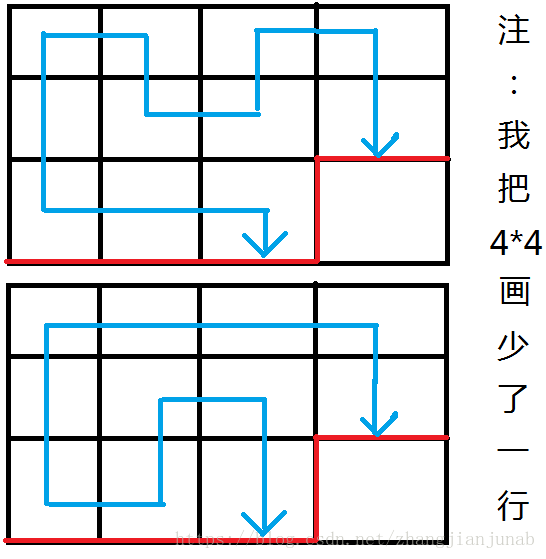
for(int j=1;j<=dp[now].size;j++)dp[now].key[j]<<=2;因為每次完成一層,輪廓線都要下降一層,如:
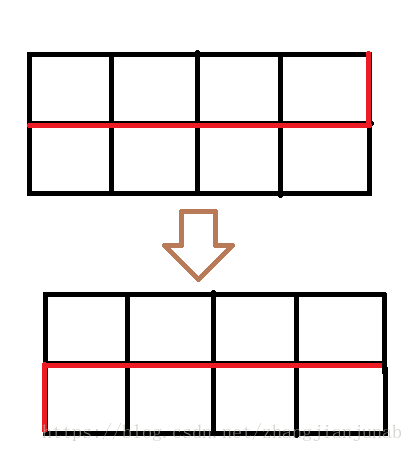
因為代碼中判斷矩陣外的格子為障礙,所以輪廓線最後那條豎線代表的是0,而且從下一行開始,一開始也沒有插頭指向開頭那條豎線(總不可能在矩陣外開插頭吧!),也為0,剛好每個狀態(除了那條豎線外)也往後一位,所以,我們就把二進位往右移兩位(因為每個括弧要兩個二進位數表示)來表示一層向下一層的轉移!
那麼,插頭DP就解決啦!