m個蘋果放在n個盤子中有多少種結果

題目

m個蘋果放在n個盤子中有多少種結果，前置條件：

• 允許存在空盤
• 重覆的擺放結果忽略不計
  

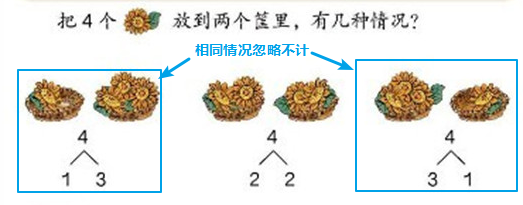
根據題意，也就是有3種情況，的確完全重覆的擺放方式是沒多大意義的

思路

這題可以用枚舉的描述方式進行尾遞歸求解：

• 情況一：
  • 存在一個空盤，甚至沒有蘋果或一個蘋果，直接返回 1
• 情況二：
  • 連盤子或蘋果都沒有，直接返 0
• 情況三：
  • 可能有n個盤子只擺放了一個蘋果，m-n的擺放占位，剩下的蘋果任意擺放
• 情況四：
  • 可能n個盤子為空，n-1，減去這空盤，剩下的m個蘋果隨意放置
• btw，存在一個以上的空盤擺放方式與圖上的重覆擺放方式是等價的，尾遞歸甚至效率並不比迴圈低，說了這麼多，研究此類問的方法還是DP（動態規劃）

將上述情況三、四二者相加就是總的所有方法（結果）

實現

package com.test.dp;

import org.junit.Test;

public class AppleOnDiskTest {
    @Test
    public void main(){
        System.out.println(dp(5,0));
    }

    /**
     *
     * @param m apple
     * @param n disk
     * @return
     */
    private int dp(int m,int n){
        if (m <= 0 || n <= 0)
            return 0;
        if (m == 0 || n == 1)
            return  1;
        else
        return dp(m-n,n) + dp(m,n-1);
    }
}

模擬遞歸的方式求解方式