演算法筆記（六）：計數排序和基數排序

（一）說明

        這裡我是按自己的理解去實現的，時間複雜度和空間複雜度和演算法導論上的可能不一樣，感興趣的話參考下就行，感覺最重要的還是演算法思想。根據演算法性能去實現演算法以後再研究。

（二）計數排序

    計數排序的基本思想是：對每一個輸人元素x，確定小於x 的元素個數。 利用這一信息，就 可以直接把x放到它在輸出數組中的位置上了。 例如，如果有17個元素小於x，則x就應該在第18個輸出位置上。 當有幾個元素相同時，這一方案要略做修改。 因為不能把它們放在同一個輸出位置上。

     從這段話我們可以得出，我們要處理的事情其實就2個：

     1、獲取小於x的元素的個數k，然後將x放到k+1的位置上（當然，因為python列表的索引是從0開始的，所以代碼就沒必要+1了，直接放到索引k上就行了（就比如：有4個元素小於X，那麼此時A[4] = X就行了，因為A[0] A[1]  A[2] A[3]））

     2、處理相同元素的情況。

實現代碼：

 1 #計數排序
 2 def conutingSort(A):
 3     B = [0 for i in range(len(A))] #初始化輸出序列
 4     #2個for迴圈獲取小於X的元素的個數，5-9行
 5     for i in range(len(A)):
 6         k = 0
 7         for j in range(len(A)):
 8             if A[i] > A[j]:
 9                 k += 1
10         #這個IF else，處理同名元素的情況，B.count(A[i])返回A[i]元素出現的個數
11         if A[i] in B:
12             B[k + B.count(A[i])] = A[i]
13         else:
14             B[k] = A[i]
15     return B
16 
17 A = [5,2,4,7,1,3,2,6,-1,-6]
18 
19 print(conutingSort(A))

（三）基數排序

     感覺這種方式單獨對正整數進行排序還好，如果考慮負數和小數的問題，問題有點複雜，甚至於可能要借用其他排序演算法去處理。看演算法導論上面的意思好像也是針對正整數的排序演算法，感覺寫這本書的大牛文筆好像不太好，沒有深入淺出的感覺，或者是翻譯的文筆不行。

      基數排序，我個人的理解是，例如：對列表A = [720,328,278,356,789,234,123]進行排序

      1、先按個位數進行排序 ，得到結果[720,123,234,356,328,278,789]

      2、在第一步的基礎上，按十位數進行排序，得到結果[720,123,234,328,356,278,789]

      3、在第二步的基礎上，按百位數進行排序，得到結果[123,234,278,328,356,720,789]

     這樣，有多少位數，就執行多少輪。最重要的是：每一輪結束時，一定要更新列表，然後下一輪排序是在這個的基礎上進行的

   實現代碼：

   **就是冪，例如x**y  就是 x的y次冪

   % 返回除法的餘數

    [a for b in s for a in b] 這個是2重的列表生成式，不瞭解列表生成式的可以單獨去瞭解下

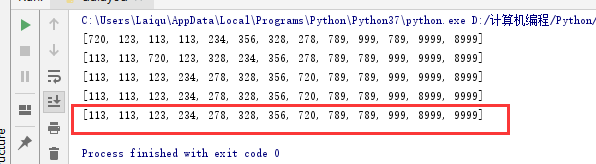
 1 #基數排序
 2 def radixSort(A, d): # 最大位數是幾，d就填幾
 3     for i in range(d):  # d輪排序
 4         s = [[] for k in range(10)]
 5         for j in A:
 6             s[int(j / (10 ** i)) % 10].append(j)
 7         A = [a for b in s for a in b] #更新列表A
 8         print(A)
 9     return A
10 
11 A = [720,328,278,356,789,234,123,113,113,999,789,9999,8999]
12 
13 print(radixSort(A,4))

可以看到，前面4個就是每一輪排序後的結果