最近在學習數據分析線性回歸演算法時,產生了很多疑問。作為初學者,我認為應該先從基本概念上進行一些深度理解。下麵將我的一些思考總結如下: 線性回歸模型為: (1) 其中ε是剩餘誤差,假設它服從的是高斯分佈,然後因此就將線性回歸模型和高斯模型聯合起來,獲取公式如下: 到這裡我是完全沒看懂! 對於線性回歸我 ...
最近在學習數據分析線性回歸演算法時,產生了很多疑問。作為初學者,我認為應該先從基本概念上進行一些深度理解。下麵將我的一些思考總結如下:
線性回歸模型為: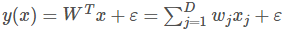 (1)
(1)
其中ε是剩餘誤差,假設它服從的是高斯分佈,然後因此就將線性回歸模型和高斯模型聯合起來,獲取公式如下:

到這裡我是完全沒看懂!
對於線性回歸我有4個疑問:
第一:看到的諸多線性回歸、邏輯回歸什麼的,回歸到底是什麼意思?
第二:這個ε剩餘誤差又有什麼樣的意義?
第三:為什麼剩餘誤差服從高斯分佈(即正態分佈),整個線性回歸模型就能寫成高斯分佈模型?
第四:這裡的線性到底指的是什麼?
接下來,我將針對這四個問題談一談自己的理解。
1. 回歸指的是什麼意思?
回歸,即將現有的數據向假設的模型擬合接近,還原真實的數據模式。
2. 如何理解ε剩餘誤差?
這裡不妨把(1)式進行合適的轉換: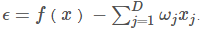 (2)
(2)
這樣就更容易理解,也就是我們只簡單地用線性模型來擬合真是的變數間的關係,並不能達到完美的解釋。所以,ε就彌補了用模型難以解釋的那一部分,即模型外的未知因素的影響。
3. 為什麼剩餘誤差符合高斯分佈,整個線性模型就符合高斯分佈?
看公式(2)應該可以較容易理解,這是純粹的數學知識。
4. 這裡的線性到底指的是什麼?
關於線性模型中的線性有三種說法:
(1)變數和參數都是線性的;
(2)變數是線性的,但參數不是線性的;
(3)參數是線性的,但變數不是線性的。
而我們這裡所說的線性模型主要是針對(3)而言的。所以只要參數是線性的這類問題,我們對變數無論是轉成指數、冪指數等任意一種函數形式,都可以用線性模型來解決問題,因為我們要學習的是這個參數向量,而變數值是確定的。



