排序演算法-（7）堆排序

堆排序

堆排序是利用堆這種數據結構而設計的一種排序演算法，堆排序是一種選擇排序，它的最壞，最好，平均時間複雜度均為O(nlogn)，它也是不穩定排序。首先簡單瞭解下堆結構。

堆是具有以下性質的完全二叉樹：每個結點的值都大於或等於其左右孩子結點的值，稱為大頂堆；或者每個結點的值都小於或等於其左右孩子結點的值，稱為小頂堆。如下圖：

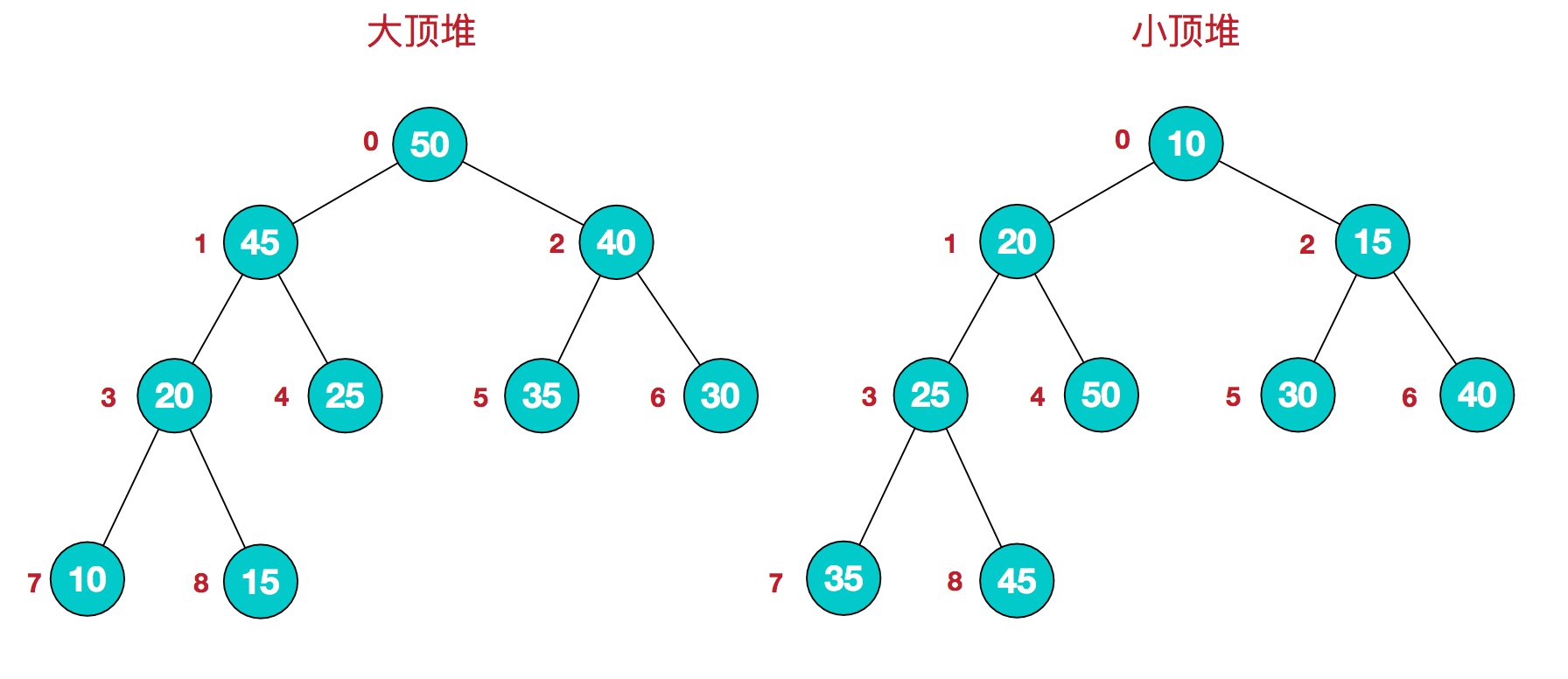
同時，我們對堆中的結點按層進行編號，將這種邏輯結構映射到數組中就是下麵這個樣子

該數組從邏輯上講就是一個堆結構，我們用簡單的公式來描述一下堆的定義就是：

大頂堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]  

小頂堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]  

詳細步驟和原理可以看這篇：https://www.cnblogs.com/chengxiao/p/6129630.html

代碼實現

//重新調整為大頂堆
function _heapify(arr, size, index) {
    let largest = index;
    const left = 2 * index + 1;
    const right = 2 * index + 2;
    if (left < size && arr[left] > arr[largest]) {
        largest = left;
    }
    if (right < size && arr[right] > arr[largest]) {
        largest = right;
    }
    if (largest !== index) {
        [arr[index], arr[largest]] = [arr[largest], arr[index]];
        _heapify(arr, size, largest);
    }
}

//這裡的堆排序用的是最大堆
function heapSort(arr) {
    const result = arr.slice(0);
    const size = arr.length;
    for (let i = Math.floor(size / 2 - 1); i >= 0; i--) {
        _heapify(result, size, i);
    }
    for (let i = size - 1; i >= 0; i--) {
        [result[0], result[i]] = [result[i], result[0]];
        _heapify(result, i, 0);
    }
    return result;
}