在Java語言的Arrays類下提供了一系列排序(sort)方法,幫助使用者對各種不同數據類型的數組進行排序. 在1.7之後的版本中, Arrays.sort()方法在操作過程中實際調用的是DualPivotQuicksort類下的sort方法,DualPivotQuicksort和Arrays一樣 ...
在Java語言的Arrays類下提供了一系列排序(sort)方法,幫助使用者對各種不同數據類型的數組進行排序. 在1.7之後的版本中, Arrays.sort()方法在操作過程中實際調用的是DualPivotQuicksort類下的sort方法,DualPivotQuicksort和Arrays一樣,都在java.util包下,按字面翻譯過來,就是雙(Dual)基準(Pivot)快速排序(Quicksort)演算法.
雙基準快速排序演算法於2009年由Vladimir Yaroslavskiy提出,是對經典快速排序(Classic Quicksort)進行優化後的一個版本, Java自1.7開始,均使用此方法作為預設排序演算法. 接下來,本文就將對此方法的具體實現過程進行簡單的介紹.
在正式進入對DualPivotQuicksort的介紹之前,我們先來對經典快速排序的實現思路進行一下簡單的瞭解:
經典快速排序在操作過程中首先會從數組中選取一個基準(Pivot),這個基準可以是數組中的任意一個元素;
隨後,將這個數組所有其他元素和Pivot進行比較,比Pivot小的數放在左側,大的數放在右側;
如此,我們就在Pivot的左側和右側各得到了一個新的數組;
接下來我們再在這兩個新的數組中各自選取新的Pivot,把小的放在左側,大的放在右側,迴圈往複,最終就會得到由小到大順序排列的數組.
下圖(via wiki)便是Quicksort的一個具體實現:
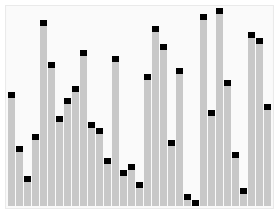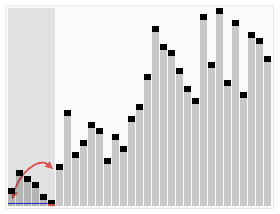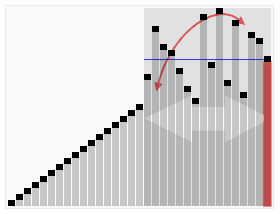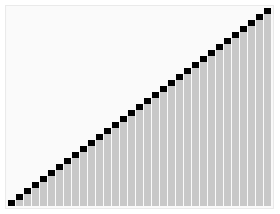
在對Quicksort的基本思路有了一定瞭解之後,下一步我們就來看Java中DualPivotQuicksort.sort是如何實現的;
本方法在實際工作過程中, 並不是對任何傳入的數組都直接進行快速排序, 而是會先對數組進行一系列測試, 然後根據數組的具體情況選擇最適合的演算法來進行排序,下麵我們結合源碼來看:
首先, 以一個int數組為例,
當一個數組int[] a被傳入DualPivotQuicksort.sort()時,該方法還會要求其他一系列參數:
1 static void sort(int[] a, int left, int right, int[] work, int workBase, int workLen)
其中,int[] a是需被排序的int數組, left和right是該數組中需要被排序的部分的左右界限. 而後面的work, workBase和workLen三個參數其實並不會參與雙基準快速排序, 而是當系統認為本數組更適合使用歸併排序(merge sort)的時候, 供歸併排序使用.
但是,在實際使用中,我們並不希望為了排序設置這麼多的參數,因此:
Arrays.sort()在調用DualPivotQuicksort.sort()之前,對int數組的排序提供了兩種參數列表:
public static void sort(int[] a)
直接對int[] a 進行排序,以及:
public static void sort(int[] a, int fromIndex, int toIndex)
對int[] a 中從fromIndex到toIndex(包頭不包尾)之間的元素進行排序.
在這裡,Arrays.sort()會自動將int[] work, int workBase, int workLen設置為null,0,0 省去了使用者的麻煩.
緊接著,DualPivotQuicksort.sort()會對傳入的int數組進行檢測, 具體流程如下: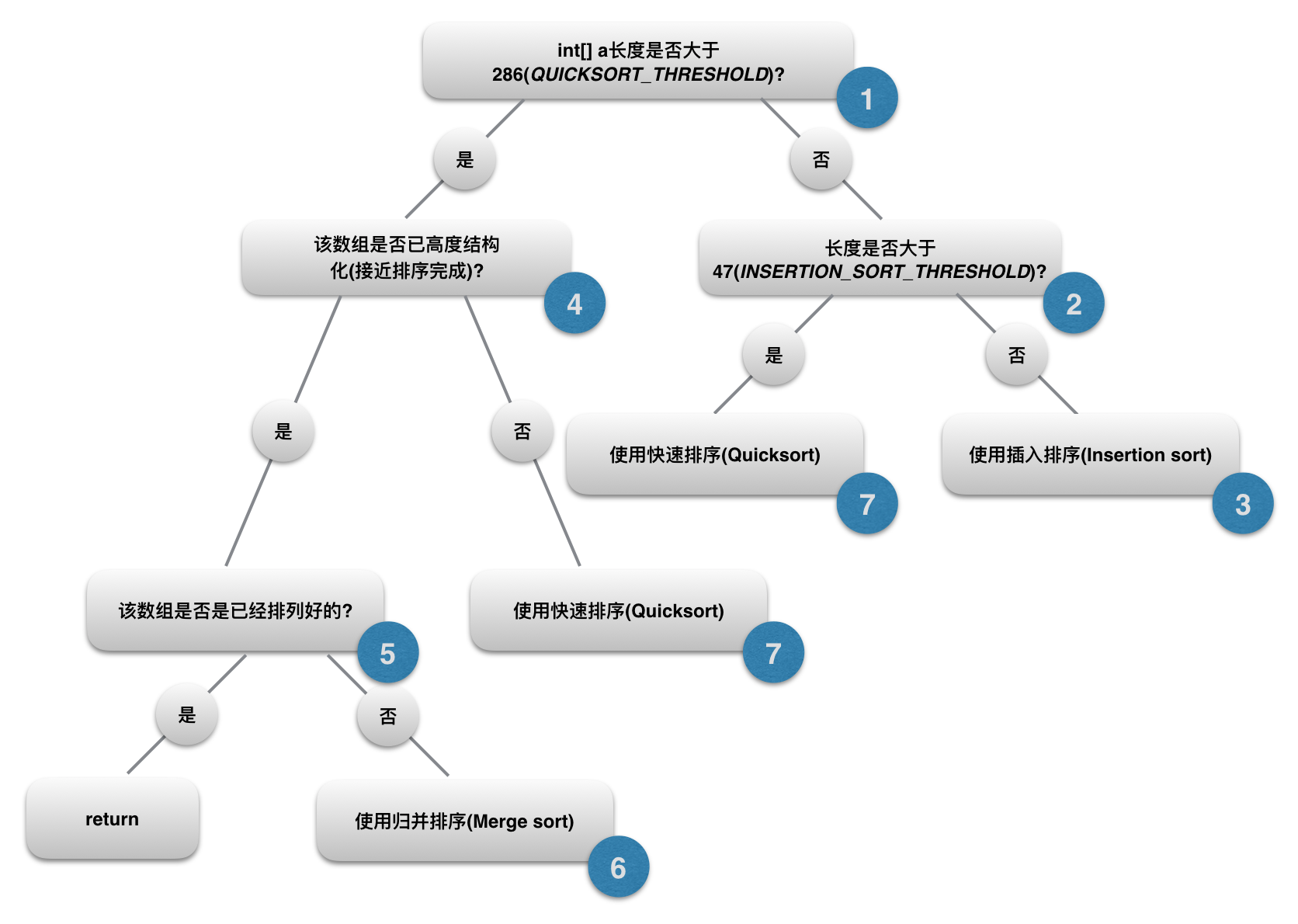
這裡先貼上整個方法的完整源碼, 然後按上圖中的流程逐步分析, 只想看DualPivotQuicksort的話可以直接跳到下麵第7點:

1 /** 2 * Sorts the specified range of the array using the given 3 * workspace array slice if possible for merging 4 * 5 * @param a the array to be sorted 6 * @param left the index of the first element, inclusive, to be sorted 7 * @param right the index of the last element, inclusive, to be sorted 8 * @param work a workspace array (slice) 9 * @param workBase origin of usable space in work array 10 * @param workLen usable size of work array 11 */ 12 static void sort(int[] a, int left, int right, 13 int[] work, int workBase, int workLen) { 14 // Use Quicksort on small arrays 15 if (right - left < QUICKSORT_THRESHOLD) { 16 sort(a, left, right, true); 17 return; 18 } 19 20 /* 21 * Index run[i] is the start of i-th run 22 * (ascending or descending sequence). 23 */ 24 int[] run = new int[MAX_RUN_COUNT + 1]; 25 int count = 0; run[0] = left; 26 27 // Check if the array is nearly sorted 28 for (int k = left; k < right; run[count] = k) { 29 if (a[k] < a[k + 1]) { // ascending 30 while (++k <= right && a[k - 1] <= a[k]); 31 } else if (a[k] > a[k + 1]) { // descending 32 while (++k <= right && a[k - 1] >= a[k]); 33 for (int lo = run[count] - 1, hi = k; ++lo < --hi; ) { 34 int t = a[lo]; a[lo] = a[hi]; a[hi] = t; 35 } 36 } else { // equal 37 for (int m = MAX_RUN_LENGTH; ++k <= right && a[k - 1] == a[k]; ) { 38 if (--m == 0) { 39 sort(a, left, right, true); 40 return; 41 } 42 } 43 } 44 45 /* 46 * The array is not highly structured, 47 * use Quicksort instead of merge sort. 48 */ 49 if (++count == MAX_RUN_COUNT) { 50 sort(a, left, right, true); 51 return; 52 } 53 } 54 55 // Check special cases 56 // Implementation note: variable "right" is increased by 1. 57 if (run[count] == right++) { // The last run contains one element 58 run[++count] = right; 59 } else if (count == 1) { // The array is already sorted 60 return; 61 } 62 63 // Determine alternation base for merge 64 byte odd = 0; 65 for (int n = 1; (n <<= 1) < count; odd ^= 1); 66 67 // Use or create temporary array b for merging 68 int[] b; // temp array; alternates with a 69 int ao, bo; // array offsets from 'left' 70 int blen = right - left; // space needed for b 71 if (work == null || workLen < blen || workBase + blen > work.length) { 72 work = new int[blen]; 73 workBase = 0; 74 } 75 if (odd == 0) { 76 System.arraycopy(a, left, work, workBase, blen); 77 b = a; 78 bo = 0; 79 a = work; 80 ao = workBase - left; 81 } else { 82 b = work; 83 ao = 0; 84 bo = workBase - left; 85 } 86 87 // Merging 88 for (int last; count > 1; count = last) { 89 for (int k = (last = 0) + 2; k <= count; k += 2) { 90 int hi = run[k], mi = run[k - 1]; 91 for (int i = run[k - 2], p = i, q = mi; i < hi; ++i) { 92 if (q >= hi || p < mi && a[p + ao] <= a[q + ao]) { 93 b[i + bo] = a[p++ + ao]; 94 } else { 95 b[i + bo] = a[q++ + ao]; 96 } 97 } 98 run[++last] = hi; 99 } 100 if ((count & 1) != 0) { 101 for (int i = right, lo = run[count - 1]; --i >= lo; 102 b[i + bo] = a[i + ao] 103 ); 104 run[++last] = right; 105 } 106 int[] t = a; a = b; b = t; 107 int o = ao; ao = bo; bo = o; 108 } 109 } 110 111 /** 112 * Sorts the specified range of the array by Dual-Pivot Quicksort. 113 * 114 * @param a the array to be sorted 115 * @param left the index of the first element, inclusive, to be sorted 116 * @param right the index of the last element, inclusive, to be sorted 117 * @param leftmost indicates if this part is the leftmost in the range 118 */ 119 private static void sort(int[] a, int left, int right, boolean leftmost) { 120 int length = right - left + 1; 121 122 // Use insertion sort on tiny arrays 123 if (length < INSERTION_SORT_THRESHOLD) { 124 if (leftmost) { 125 /* 126 * Traditional (without sentinel) insertion sort, 127 * optimized for server VM, is used in case of 128 * the leftmost part. 129 */ 130 for (int i = left, j = i; i < right; j = ++i) { 131 int ai = a[i + 1]; 132 while (ai < a[j]) { 133 a[j + 1] = a[j]; 134 if (j-- == left) { 135 break; 136 } 137 } 138 a[j + 1] = ai; 139 } 140 } else { 141 /* 142 * Skip the longest ascending sequence. 143 */ 144 do { 145 if (left >= right) { 146 return; 147 } 148 } while (a[++left] >= a[left - 1]); 149 150 /* 151 * Every element from adjoining part plays the role 152 * of sentinel, therefore this allows us to avoid the 153 * left range check on each iteration. Moreover, we use 154 * the more optimized algorithm, so called pair insertion 155 * sort, which is faster (in the context of Quicksort) 156 * than traditional implementation of insertion sort. 157 */ 158 for (int k = left; ++left <= right; k = ++left) { 159 int a1 = a[k], a2 = a[left]; 160 161 if (a1 < a2) { 162 a2 = a1; a1 = a[left]; 163 } 164 while (a1 < a[--k]) { 165 a[k + 2] = a[k]; 166 } 167 a[++k + 1] = a1; 168 169 while (a2 < a[--k]) { 170 a[k + 1] = a[k]; 171 } 172 a[k + 1] = a2; 173 } 174 int last = a[right]; 175 176 while (last < a[--right]) { 177 a[right + 1] = a[right]; 178 } 179 a[right + 1] = last; 180 } 181 return; 182 } 183 184 // Inexpensive approximation of length / 7 185 int seventh = (length >> 3) + (length >> 6) + 1; 186 187 /* 188 * Sort five evenly spaced elements around (and including) the 189 * center element in the range. These elements will be used for 190 * pivot selection as described below. The choice for spacing 191 * these elements was empirically determined to work well on 192 * a wide variety of inputs. 193 */ 194 int e3 = (left + right) >>> 1; // The midpoint 195 int e2 = e3 - seventh; 196 int e1 = e2 - seventh; 197 int e4 = e3 + seventh; 198 int e5 = e4 + seventh; 199 200 // Sort these elements using insertion sort 201 if (a[e2] < a[e1]) { int t = a[e2]; a[e2] = a[e1]; a[e1] = t; } 202 203 if (a[e3] < a[e2]) { int t = a[e3]; a[e3] = a[e2]; a[e2] = t; 204 if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; } 205 } 206 if (a[e4] < a[e3]) { int t = a[e4]; a[e4] = a[e3]; a[e3] = t; 207 if (t < a[e2]) { a[e3] = a[e2]; a[e2] = t; 208 if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; } 209 } 210 } 211 if (a[e5] < a[e4]) { int t = a[e5]; a[e5] = a[e4]; a[e4] = t; 212 if (t < a[e3]) { a[e4] = a[e3]; a[e3] = t; 213 if (t < a[e2]) { a[e3] = a[e2]; a[e2] = t; 214 if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; } 215 } 216 } 217 } 218 219 // Pointers 220 int less = left; // The index of the first element of center part 221 int great = right; // The index before the first element of right part 222 223 if (a[e1] != a[e2] && a[e2] != a[e3] && a[e3] != a[e4] && a[e4] != a[e5]) { 224 /* 225 * Use the second and fourth of the five sorted elements as pivots. 226 * These values are inexpensive approximations of the first and 227 * second terciles of the array. Note that pivot1 <= pivot2. 228 */ 229 int pivot1 = a[e2]; 230 int pivot2 = a[e4]; 231 232 /* 233 * The first and the last elements to be sorted are moved to the 234 * locations formerly occupied by the pivots. When partitioning 235 * is complete, the pivots are swapped back into their final 236 * positions, and excluded from subsequent sorting. 237 */ 238 a[e2] = a[left]; 239 a[e4] = a[right]; 240 241 /* 242 * Skip elements, which are less or greater than pivot values. 243 */ 244 while (a[++less] < pivot1); 245 while (a[--great] > pivot2); 246 247 /* 248 * Partitioning: 249 * 250 * left part center part right part 251 * +--------------------------------------------------------------+ 252 * | < pivot1 | pivot1 <= && <= pivot2 | ? | > pivot2 | 253 * +--------------------------------------------------------------+ 254 * ^ ^ ^ 255 * | | | 256 * less k great 257 * 258 * Invariants: 259 * 260 * all in (left, less) < pivot1 261 * pivot1 <= all in [less, k) <= pivot2 262 * all in (great, right) > pivot2 263 * 264 * Pointer k is the first index of ?-part. 265 */ 266 outer: 267 for (int k = less - 1; ++k <= great; ) { 268 int ak = a[k]; 269 if (ak < pivot1) { // Move a[k] to left part 270 a[k] = a[less]; 271 /* 272 * Here and below we use "a[i] = b; i++;" instead 273 * of "a[i++] = b;" due to performance issue. 274 */ 275 a[less] = ak; 276 ++less; 277 } else if (ak > pivot2) { // Move a[k] to right part 278 while (a[great] > pivot2) { 279 if (great-- == k) { 280 break outer; 281 } 282 } 283 if (a[great] < pivot1) { // a[great] <= pivot2 284 a[k] = a[less]; 285 a[less] = a[great]; 286 ++less; 287 } else { // pivot1 <= a[great] <= pivot2 288 a[k] = a[great]; 289 } 290 /* 291 * Here and below we use "a[i] = b; i--;" instead 292 * of "a[i--] = b;" due to performance issue. 293 */ 294 a[great] = ak; 295 --great; 296 } 297 } 298 299 // Swap pivots into their final positions 300 a[left] = a[less - 1]; a[less - 1] = pivot1; 301 a[right] = a[great + 1]; a[great + 1] = pivot2; 302 303 // Sort left and right parts recursively, excluding known pivots 304 sort(a, left, less - 2, leftmost); 305 sort(a, great + 2, right, false); 306 307 /* 308 * If center part is too large (comprises > 4/7 of the array), 309 * swap internal pivot values to ends. 310 */ 311 if (less < e1 && e5 < great) { 312 /* 313 * Skip elements, which are equal to pivot values. 314 */ 315 while (a[less] == pivot1) { 316 ++less; 317 } 318 319 while (a[great] == pivot2) { 320 --great; 321 } 322 323 /* 324 * Partitioning: 325 * 326 * left part center part right part 327 * +----------------------------------------------------------+ 328 * | == pivot1 | pivot1 < && < pivot2 | ? | == pivot2 | 329 * +----------------------------------------------------------+ 330 * ^ ^ ^ 331 * | | | 332 * less k great 333 * 334 * Invariants: 335 * 336 * all in (*, less) == pivot1 337 * pivot1 < all in [less, k) < pivot2 338 * all in (great, *) == pivot2 339 * 340 * Pointer k is the first index of ?-part. 341 */ 342 outer: 343 for (int k = less - 1; ++k <= great; ) { 344 int ak = a[k]; 345 if (ak == pivot1) { // Move a[k] to left part 346 a[k] = a[less]; 347 a[less] = ak; 348 ++less; 349 } else if (ak == pivot2) { // Move a[k] to right part 350 while (a[great] == pivot2) { 351 if (great-- == k) { 352 break outer; 353 } 354 } 355 if (a[great] == pivot1) { // a[great] < pivot2 356 a[k] = a[less]; 357 /* 358 * Even though a[great] equals to pivot1, the 359 * assignment a[less] = pivot1 may be incorrect, 360 * if a[great] and pivot1 are floating-point zeros 361 * of different signs. Therefore in float and 362 * double sorting methods we have to use more 363 * accurate assignment a[less] = a[great]. 364 */ 365 a[less] = pivot1; 366 ++less; 367 } else { // pivot1 < a[great] < pivot2 368 a[k] = a[great]; 369 } 370 a[great] = ak; 371 --great; 372 } 373 } 374 } 375 376 // Sort center part recursively 377 sort(a, less, great, false); 378 379 } else { // Partitioning with one pivot 380 /* 381 * Use the third of the five sorted elements as pivot. 382 * This value is inexpensive approximation of the median. 383 */ 384 int pivot = a[e3]; 385 386 /* 387 * Partitioning degenerates to the traditional 3-way 388 * (or "Dutch National Flag") schema: 389 * 390 * left part center part right part 391 * +-------------------------------------------------+ 392 * | < pivot | == pivot | ? | > pivot | 393 * +-------------------------------------------------+ 394 * ^ ^ ^ 395 * | | | 396 * less k great 397 * 398 * Invariants: 399 * 400 * all in (left, less) < pivot 401 * all in [less, k) == pivot 402 * all in (great, right) > pivot 403 * 404 * Pointer k is the first index of ?-part. 405 */ 406 for (int k = less; k <= great; ++k) { 407 if (a[k] == pivot) { 408 continue; 409 } 410 int ak = a[k]; 411 if (ak < pivot) { // Move a[k] to left part 412 a[k] = a[less]; 413 a[less] = ak; 414 ++less; 415 } else { // a[k] > pivot - Move a[k] to right part 416 while (a[great] > pivot) { 417 --great; 418 } 419 if (a[great] < pivot) { // a[great] <= pivot 420 a[k] = a[less]; 421 a[less] = a[great]; 422 ++less; 423 } else { // a[great] == pivot 424 /* 425 * Even though a[great] equals to pivot, the 426 * assignment a[k] = pivot may be incorrect, 427 * if a[great] and pivot are floating-point 428 * zeros of different signs. Therefore in float 429 * and double sorting methods we have to use 430 * more accurate assignment a[k] = a[great]. 431 */ 432 a[k] = pivot; 433 } 434 a[great] = ak; 435 --great; 436 } 437 } 438 439 /* 440 * Sort left and right parts recursively. 441 * All elements from center part are equal 442 * and, therefore, already sorted. 443 */ 444 sort(a, left, less - 1, leftmost); 445 sort(a, great + 1, right, false); 446 } 447 }DualPivotQuickSort.sort()
1. 判斷數組int[] a的長度是否大於常量QUICKSORT_THRESHOLD, 即286:
286是java設定的一個閾值,當數組長度小於此值時, 系統將不再考慮merge sort, 直接將參數傳入本類中的另一個私有sort方法進行排序,
private static void sort(long[] a, int left, int right, boolean leftmost)

1 // Use Quicksort on small arrays 2 if (right - left < QUICKSORT_THRESHOLD) { 3 sort(a, left, right, true); 4 return; 5 }判斷數組int[] a的長度是否大於常量QUICKSORT_THRESHOLD
2. 繼續判斷int[] a的長度是否大於常量INSERTION_SORT_THRESHOLD, 即47:
3. 若數組長度小於47, 則使用insertion sort:
數組傳入本類私有的sort方法後, 會繼續判斷數組長度是否大於47, 若小於此值, 則直接使用insertion sort並返回結果, 因為插入演算法並非本文重點, 此處不再展開敘述,

1 int length = right - left + 1; 2 3 // Use insertion sort on tiny arrays 4 if (length < INSERTION_SORT_THRESHOLD) {



