【學時總結】 ◆學時·III◆ 二分圖

-Advertisement-

圖論是演算法競賽的一大板塊，二分圖又是其中一個重要的特殊模型——好像有點像網路流QwQ 例題：eXam(SGU 172)、The Perfect Stall(POJ 1274)、Machine Schedule(POJ 1325) ...

【學時·III】二分圖

■基本策略■

其實本質是圖論中的網路流

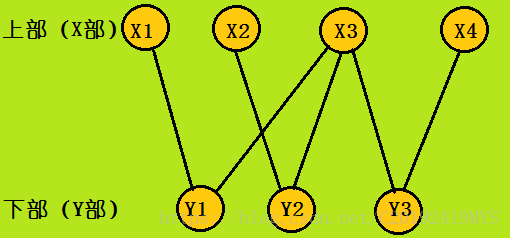
二分圖是兩個由多個點組成的集合（上部和下部，且沒有重疊），兩個集合中的點不與該集合內其他的點連通，但和另一個集合內的點連通。我們稱這兩個集合為上部、下部，或X、Y部，比如：
這裡寫圖片描述

判定

我們可以通過染色的方法將一個普通的連通圖轉換為二分圖（如果不是連通圖，則說明該圖存在多個二分圖或不為二分圖）。由於X部只與Y部相連，Y部也只與X部相連，我們可以把X、Y部染成不同的顏色。通過BFS(DFS也可以)從圖裡的一個點開始，假設它為X部，則與它相連的點為Y部，之後又為X部……直到訪問到一個標記過的點，且該點的標記與將要作的標記不同，則不是二分圖。將所有點標記完後還沒有衝突，則是二分圖。

演算法

與二分圖相關的有匈牙利演算法、König定理，分別處理增廣路和最大匹配問題。

最大匹配

二分圖中若存在邊集 E() 使得其中的邊沒有交點（共同的頂點），則稱 E() 是該二分圖的一個匹配。

特別的，若 E() 所含的頂點恰好是二分圖中所有的頂點，則稱 E() 為完全匹配。

最常考的是最大匹配，此時 E() 所包含的邊的數量達到二分圖中可能的最大數量。

增廣路徑

邊集 E() 為二分圖已經匹配的邊，路徑P連接不同部的未匹配的點，若在P中匹配的邊和未匹配的邊交替出現，則稱P為增廣路徑。可見P的邊數一定是奇數，且因為起點和終點都未匹配，所以匹配邊比未匹配邊少1。

通過將增廣路徑反色——未匹配邊換為匹配邊，匹配邊換為未匹配邊，我們可以得到一個更好的匹配。當沒有增廣路徑時，形成的匹配就是該二分圖的最大匹配。

這種演算法稱為匈牙利演算法。

■來一點版題■

◆沒有技術含量◆ eXam

只要知道二分圖的定義就可以了

SGU - 172
解析

這道題只需要判斷給出的數據是否合法，且數據完美地分為X部（考試）、Y部（學生），因此就是一個標準的非連通圖二分圖判斷。

考試與學生的關係可以看做連線，這樣我們就得到了一個圖，其實是多個圖。可以通過遍歷每一個沒有標記的點來判別每一個連通圖是否都是二分圖，只要有一個不是，就判斷"no"。這裡作者用vector 的鄰接表儲存圖，col[] 儲存標記。
這裡的方案其實就是X、Y部中的某一部。(⊙_⊙)

源代碼

/*Lucky_Glass*/
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<vector>
using namespace std;
int n_cla,n_stu,col[30005],error;
vector<int> vec[30005];
vector<int> ans;
void Solve(int u,int c)
{
    col[u]=c;
    if(c%2) ans.push_back(u);
    for(int i=0;i<(int)vec[u].size();i++)
    {
        int v=vec[u][i];
        if(col[v]){if((c+1)%2!=col[v]%2)error=true;continue;}
        Solve(v,c+1);
        if(error) return;
    }
}
int main()
{
    scanf("%d%d",&n_cla,&n_stu);
    for(int i=1;i<=n_stu;i++)
    {
        int A,B;scanf("%d%d",&A,&B);
        vec[B].push_back(A);vec[A].push_back(B);
    }
    for(int i=1;i<=n_cla;i++)
        if(!col[i])
        {
            Solve(i,1);
            if(error)
            {
                puts("no");
                return 0;
            }
        }
    printf("yes\n%d\n%d",ans.size(),ans[0]);
    for(int i=1;i<(int)ans.size();i++)
        printf(" %d",ans[i]);
    return 0;
}

◆最大匹配◆ The Perfect Stall

把匈牙利演算法的板套上去

POJ - 1274
解析

圖的建立

雖然二分圖分為2個部（牛欄、奶牛），但實際上它還是一個圖——所以必須將2個部的點放入同一個圖中。這裡可以通過將牛放入1~N的點，把牛欄放入N+1~N+M的點中。

匈牙利演算法的實現

尋找增廣路徑一般是採用DFS：

bool DFS(int u)
{
    for(int i=0;i<(int)vec[u].size();i++) //枚舉鄰接點
    {
        int v=vec[u][i];
        if(vis[v]) continue; //之前沒有訪問
        vis[v]=true; //標記
        if(mat[v]==0 || DFS(mat[v])) //如果該點沒有匹配，或通過該點能向下找到一個未匹配點
        { //這就是一條增廣路徑
            mat[u]=v;mat[v]=u; //反邊
            return true;
        }
    }
    return false;
}

這道題比較基礎，只要求找到最大匹配的數量，因此直接使用匈牙利演算法，統計有多少組匹配就可以了。

源代碼

/*Lucky_Glass*/
#include<cstdio>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;
#define MAXN 200
int n,m,mat[2*MAXN+5];
bool vis[2*MAXN+5];
vector<int> vec[2*MAXN+5];
bool DFS(int u)
{
    for(int i=0;i<(int)vec[u].size();i++)
    {
        int v=vec[u][i];
        if(vis[v]) continue;
        vis[v]=true;
        if(mat[v]==0 || DFS(mat[v]))
        {
            mat[u]=v;mat[v]=u;
            return true;
        }
    }
    return false;
}
int Solve()
{
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        memset(vis,false,sizeof vis);
        if(mat[i]==0 && DFS(i))
            ans++;
    }
    return ans;
}
int main()
{
    while(scanf("%d%d",&n,&m)==2)
    {
        memset(mat,0,sizeof mat);
        for(int i=1;i<=n;i++)
        {
            int n_;scanf("%d",&n_);
            for(int j=0,x;j<n_;j++)
            {
                scanf("%d",&x);
                vec[i].push_back(x+n);
                vec[x+n].push_back(i);
            }
        }
        printf("%d\n",Solve());
        for(int i=1;i<=n;i++) vec[i].erase(vec[i].begin(),vec[i].end());
        for(int i=1;i<=m;i++) vec[i+n].erase(vec[i+n].begin(),vec[i+n].end());
    }
    return 0;
}

◆最小覆蓋◆ Machine Schedule

就像一道結論題，結論一發現，就沒什麼難點了

POJ - 1325
解析

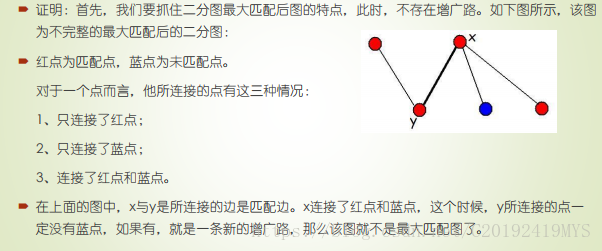
König定理

最小覆蓋點數=最大匹配數

下麵是證明：
這裡寫圖片描述

所以這道題還是最大匹配~

源代碼

/*Lucky_Glass*/
#include<cstdio>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;
#define MAXN 200
int n,m,mat[2*MAXN+5];
bool vis[2*MAXN+5];
vector<int> vec[2*MAXN+5];
bool DFS(int u)
{
    for(int i=0;i<(int)vec[u].size();i++)
    {
        int v=vec[u][i];
        if(vis[v]) continue;
        vis[v]=true;
        if(mat[v]==0 || DFS(mat[v]))
        {
            mat[u]=v;mat[v]=u;
            return true;
        }
    }
    return false;
}
int Solve()
{
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        memset(vis,false,sizeof vis);
        if(mat[i]==0 && DFS(i))
            ans++;
    }
    return ans;
}
int main()
{
    while(scanf("%d%d",&n,&m)==2)
    {
        memset(mat,0,sizeof mat);
        for(int i=1;i<=n;i++)
        {
            int n_;scanf("%d",&n_);
            for(int j=0,x;j<n_;j++)
            {
                scanf("%d",&x);
                vec[i].push_back(x+n);
                vec[x+n].push_back(i);
            }
        }
        printf("%d\n",Solve());
        for(int i=1;i<=n;i++) vec[i].erase(vec[i].begin(),vec[i].end());
        for(int i=1;i<=m;i++) vec[i+n].erase(vec[i+n].begin(),vec[i+n].end());
    }
    return 0;
}

The End

Thanks for reading!

- Lucky_Glass

您的分享是我們最大的動力!