3 插值與曲線擬合

Interpolation and Curve Fitting
給定n+1個數據點(xi,yi), i = 0,1,2,…,n，評估y(x).

3.1 介紹（introduction）

離散數據集，或者形如下麵的表格，常常在技術計算中用到，數據源可能來自於實驗觀察或者數值計算。

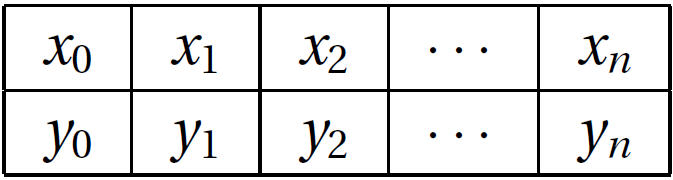
3.2 多項式插值（Polynomial Interpolation）
插值和曲線擬合存在差別。對於插值，我們通過數據擬合一條曲線，在擬合過程中，我們潛在假設數據是精確的和獨特的；對於曲線擬合，使用的數據通常存在測量誤差而引入了雜訊，在某種程度上，我們想發現一條光滑的曲線近似數據點，進而，曲線不必穿過每個數據點。插值和曲線擬合的區別如下圖：

Lagrange’s Method拉格朗如方法
插值最簡單的形式是多項式，經過n+1個明確的數據點，構建一個自由度為n的特定多項式總是可以實現的。包含這個多項式的方法就是朗格朗日方程：

其中基函數（cardinal function）li(x)如下：

• 例子1：n=1，p1(x)=y0l0(x)+y1l1(x)
  
• 例子2：n=2,
  

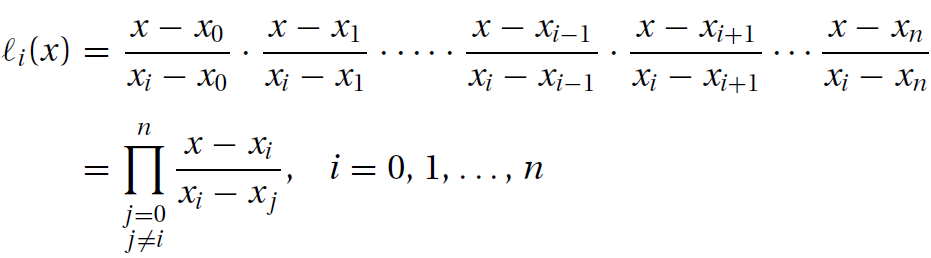
通過觀察，基函數具有如下性質

• 是一個自由度為n的多項式
• 
  註：Kronecker delta (δij)，當n=2，x0=0,x1=2,x2=3時，性質如下圖
  

多項式插值誤差如下：

ξ位於區間(x0,xn)

牛頓方法Newton’s Method
牛頓方法的插值多項式如下：

對於有四個數據點n=3，多項式如下：

n=3，利於編程，定義如下形式：

n，定義如下：

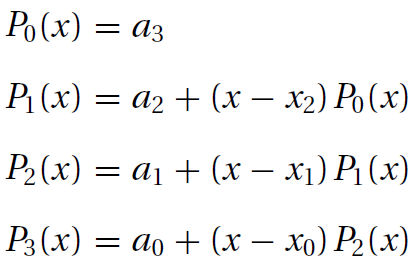
Denoting the x-coordinate array of the data points by xData and the degree of the polynomial by n, we have the following algorithm for computing Pn(x):

p = a[n]
for k in range(1, n+1):
    p = a[n-k] + (x - xData[n-k])*p

繫數Pn迫使多項式通過每一個數據點：yi=Pn(xi), i=0,1,...,n。則下麵的方程同時發生：

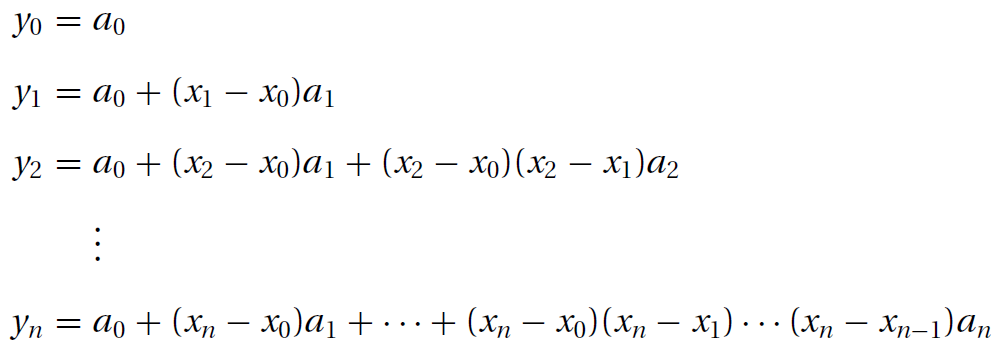
引入均差概念(divided differences)

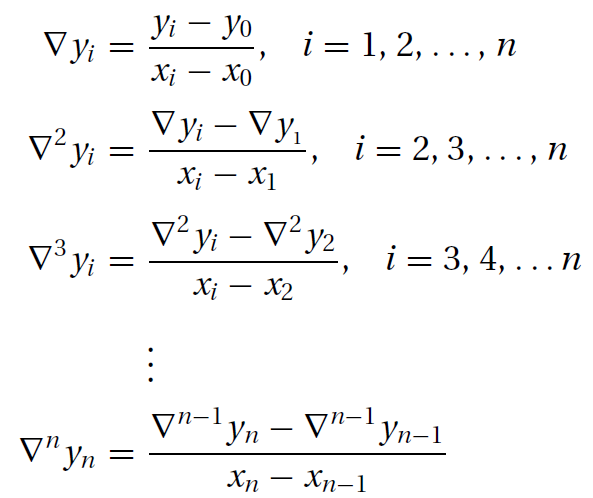
則有：

對於n=4，手工計算繫數，可以通過如下表格快速解決：

正好是多項式的繫數。

Machine computations can be carried out within a one-dimensional array a employing the following algorithm (we use the notation m = n + 1 = number of data points):
Python 計算流程如下：

a = yData.copy()
for k in range(1,m):
    for i in range(k, m):
        a[i] = (a[i] - a[k-1])/(xData[i] - xData[k-1])

最初，a包含數據的y坐標，因此它與上表中的第二列相同。 每次通過外部迴圈時，都會在下一列中生成條目，這會覆蓋a的相應元素。 因此，結束包含上表中的對角項（即多項式的繫數）。

牛頓多項式插值方法的Python代碼
Newton’s method. Given the data point arrays xData and yData, the function coeffts returns the coefficient array a. After the coefficients are found, the interpolant Pn(x) can be evaluated at any value of x with the function evalPoly.

def evalPoly(a, xData, x):
    n = len(xData) - 1
    p = a[n]
    for k in range(1, n+1):
        p = a[n-k]  + (x - xData[n-k])*p
    return p

def coeffts(xData, yData):
    m = len(xData)
    a = yData.copy()
    for k in range(1,m):
        a[k:m] = (a[k:m] - a[k-1]) / (xData[k:m] - xData[k-1])
    return a

參考翻譯《Numerical Methods in Engineering with Python 3》