恢復內容開始 作者 : liuyang0 來源 : 博客園 常見排序演算法總結與實現 本文使用Java實現這幾種排序。以下是對排序演算法總體的介紹。 冒泡排序 時間複雜度:O(n^2),最優時間複雜度:O(n),平均時間複雜度:O(n^2) 插入排序 時間複雜度:O(n^2),最優時間複雜度:O(n), ...
---恢復內容開始---
作者 : liuyang0
來源 : 博客園
常見排序演算法總結與實現
本文使用Java實現這幾種排序。
以下是對排序演算法總體的介紹。
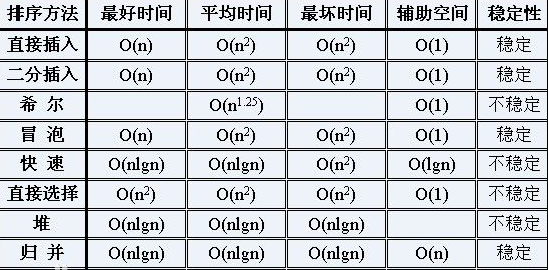
冒泡排序
- 比較相鄰的元素。如果第一個比第二個大,就交換他們兩個。
- 對每一對相鄰元素作同樣的工作,從開始第一對到結尾的最後一對。這步做完後,最後的元素會是最大的數。
- 針對所有的元素重覆以上的步驟,除了最後一個。
- 持續每次對越來越少的元素重覆上面的步驟,直到沒有任何一對數字需要比較。
時間複雜度:O(n^2),最優時間複雜度:O(n),平均時間複雜度:O(n^2)

1public static void bubbleSort(Comparable[] a) {
2 int j, flag;
3 Comparable temp;
4 for (int i = 0; i < a.length; i++) {
5 flag = 0;
6 for (j = 1; j < a.length - i; j++) {
7 if (a[j].compareTo(a[j - 1]) < 0) {
8 temp = a[j];
9 a[j] = a[j - 1];
10 a[j - 1] = temp;
11 flag = 1;
12 }
13 }
14 // 如果沒有交換,代表已經排序完畢,直接返回
15 if (flag == 0) {
16 return;
17 }
18 }
19}
插入排序
- 從第一個元素開始,該元素可以認為已經被排序
- 取出下一個元素,在已經排序的元素序列中從後向前掃描
- 如果該元素(已排序)大於新元素,將該元素移到下一位置
- 重覆步驟3,直到找到已排序的元素小於或者等於新元素的位置
- 將新元素插入到該位置後
- 重覆步驟2~5
時間複雜度:O(n^2),最優時間複雜度:O(n),平均時間複雜度:O(n^2)

下麵展示了三種插入排序的實現,第二種方法減少了交換次數,第三種採用二分查找法查到插入點。
1public static void insertionSort(Comparable[] a) {
2 int length = a.length;
3 Comparable temp;
4 for (int i = 1; i < length; i++) {
5 for (int j = i; j > 0 && a[j].compareTo(a[j - 1]) < 0; j--) {
6 temp = a[j];
7 a[j] = a[j - 1];
8 a[j - 1] = temp;
9 }
10 }
11}
12
13// 對實現Comparable的類型進行排序,先將大的元素都向右移動,減少一半交換次數
14public static void insertionSort(Comparable[] a) {
15 int length = a.length;
16 Comparable temp;
17 int j;
18 for (int i = 1; i < length; i++) {
19 temp = a[i];
20 for (j = i; j > 0 && temp.compareTo(a[j - 1]) < 0; j--) {
21 a[j] = a[j - 1];
22 }
23 a[j] = temp;
24 }
25}
26
27// 二分插入排序,使用二分查找找到插入點,然後進行移位
28public static void insertionSort(Comparable[] a) {
29 int length = a.length;
30 Comparable temp;
31 int j;
32 for (int i = 1; i < length; i++) {
33 if (a[i].compareTo(a[i - 1]) < 0) {
34 temp = a[i];
35 int index = binarySearch(a, a[i], 0, i - 1);
36 for (j = i - 1; j >= index; j--) {
37 a[j + 1] = a[j];
38 }
39 a[index] = temp;
40 }
41 }
42}
43
44private static int binarySearch(Comparable[] a, Comparable target, int start, int end) {
45 int mid;
46 while (start <= end) {
47 mid = (start + end) >> 1;
48 if (target.compareTo(a[mid]) < 0) {
49 end = mid - 1;
50 } else {
51 start = mid + 1;
52 }
53 }
54 return start;
55}
選擇排序
首先在未排序序列中找到最小元素,存放到排序序列的起始位置,然後,再從剩餘未排序元素中繼續尋找最小元素,然後放到已排序序列的末尾。
時間複雜度:O(n^2),最優時間複雜度:O(n^2),平均時間複雜度:O(n^2)

1public static void selectionSort1(Comparable[] a) {
2 int length = a.length;
3 int min;
4 Comparable temp;
5 for (int i = 0; i < length; i++) {
6 min = i;
7 for (int j = i + 1; j < length; j++) {
8 if (a[j].compareTo(a[min]) < 0) {
9 min = j;
10 }
11 }
12 temp = a[min];
13 a[min] = a[i];
14 a[i] = temp;
15 }
16}
希爾排序
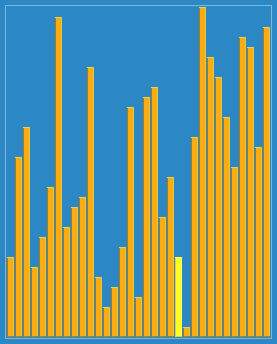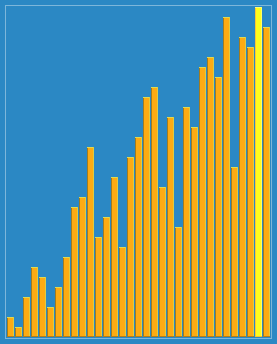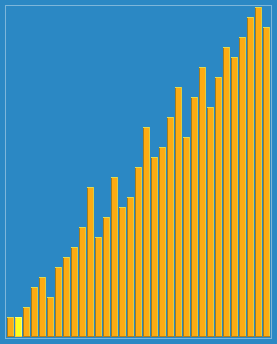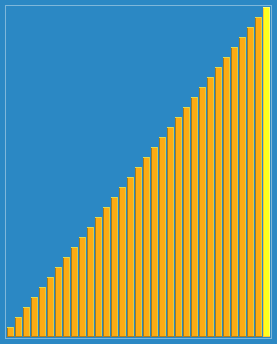
希爾排序通過將比較的全部元素分為幾個區域來提升插入排序的性能。這樣可以讓一個元素可以一次性地朝最終位置前進一大步。然後演算法再取越來越小的步長進行排序,演算法的最後一步就是普通的插入排序,但是到了這步,需排序的數據幾乎是已排好的了(此時插入排序較快)。
時間複雜度:根據步長而不同,最優時間複雜度:O(n),平均時間複雜度:根據步長而不同
1public static void shellSort(Comparable[] a) {
2 int length = a.length;
3 int h = 1;
4 Comparable temp;
5 while (h < length / 3) {
6 h = 3 * h + 1;
7 }
8 while (h >= 1) {
9 for (int i = h; i < length; i++) {
10 for (int j = i; j >= h && a[j].compareTo(a[j - h]) < 0; j -= h) {
11 temp = a[j];
12 a[j] = a[j - h];
13 a[j - h] = temp;
14 }
15 }
16 h /= 3;
17 }
18}
堆排序
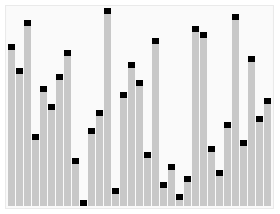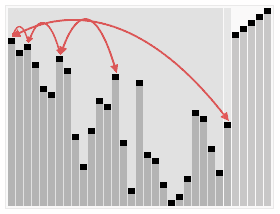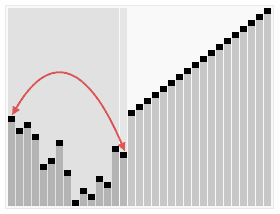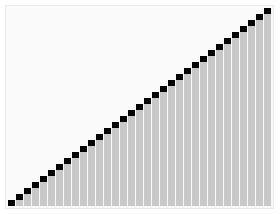
- 創建最大堆(Build_Max_Heap):將堆所有數據重新排序
- 堆排序(HeapSort):移除位在第一個數據的根節點,並做最大堆調整的遞歸運算
時間複雜度:O(nlogn),最優時間複雜度:O(nlogn),平均時間複雜度:O(nlogn)
1public static void heapSort(Comparable[] a) {
2 int length = a.length;
3 Comparable temp;
4 for (int k = length / 2; k >= 1; k--) {
5 sink(a, k, length);
6 }
7 while (length > 0) {
8 temp = a[0];
9 a[0] = a[length - 1];
10 a[length - 1] = temp;
11 length--;
12 sink(a, 1, length);
13 }
14}
15
16private static void sink(Comparable[] a, int k, int n) {
17 Comparable temp;
18 while (2 * k <= n) {
19 int j = 2 * k;
20 if (j < n && a[j - 1].compareTo(a[j]) < 0) {
21 j++;
22 }
23 if (a[k - 1].compareTo(a[j - 1]) >= 0) {
24 break;
25 }
26 temp = a[k - 1];
27 a[k - 1] = a[j - 1];
28 a[j - 1] = temp;
29 k = j;
30 }
31}
歸併排序
歸併操作(merge),也叫歸併演算法,指的是將兩個已經排序的序列合併成一個序列的操作。歸併排序演算法依賴歸併操作。
時間複雜度:O(nlogn),最優時間複雜度:O(n),平均時間複雜度:O(nlogn),空間複雜度O(n)

自頂向下的歸併排序
1private static Comparable[] aux;
2// 自頂向下
3public static void mergeSort(Comparable[] a) {
4 aux = new Comparable[a.length];
5 mergeSort(a, 0, a.length - 1);
6}
7
8public static void mergeSort(Comparable[] a, int lo, int hi) {
9 if (hi <= lo) {
10 return;
11 }
12 int mid = (lo + hi) >>> 1;
13 mergeSort(a, lo, mid);
14 mergeSort(a, mid + 1, hi);
15 merge(a, lo, mid, hi);
16}
17
18public static void merge(Comparable[] a, int lo, int mid, int hi) {
19 int i = lo, j = mid + 1;
20
21 for (int k = lo; k <= hi; k++) {
22 aux[k] = a[k];
23 }
24
25 for (int k = lo; k <= hi; k++) {
26 if



