lavaan簡明教程 [中文翻譯版] 譯者註:此文檔原作者為比利時Ghent大學的Yves Rosseel博士,lavaan亦為其開發,完全開源、免費。我在學習的時候順手翻譯了一下,向Yves的開源精神致敬。此翻譯因偷懶部分刪減,但也有增加,有錯誤請留言 「轉載請註明出處」 目錄 lavaan簡明教 ...
lavaan簡明教程 [中文翻譯版]
譯者註:此文檔原作者為比利時Ghent大學的Yves Rosseel博士,lavaan亦為其開發,完全開源、免費。我在學習的時候順手翻譯了一下,向Yves的開源精神致敬。此翻譯因偷懶部分刪減,但也有增加,有錯誤請留言
「轉載請註明出處」
目錄
lavaan簡明教程 [中文翻譯版]
目錄
摘要
- 在開始之前
- 安裝lavaan包
- 模型語法
- 例1:驗證性因數分析(CFA)
- 例2:結構方程(SEM)
- 更多關於語法的內容
6.1 固定參數
6.2 初值
6.3 參數標簽
6.4 修改器
6.5 簡單相等約束
6.6 非線性相等和不相等約束 - 引入平均值
- 結構方程的多組分析
8.1 在部分組中固定參數
8.2 約束一個參數使其在各組中相等
8.3 約束一組參數使其在各組中相等
8.4 測量不變性 - 增長曲線模型
- 使用分類變數
- 將協方差矩陣作為輸入
- 估計方法,標準誤差和缺失值
12.1 估計方法
12.2 最大似然估計
12.3 缺失值 - 間接效應和中介分析
- 修正指標
- 從擬合方程中提取信息
摘要
此教程首先介紹lavaan的基本組成部分:模型語法,擬合方程(CFA, SEM和growth),用來呈現結果的主要函數(summary, coef, fitted, inspect);
然後提供兩個實例;
最後再討論一些重要話題:均值結構模型(meanstructures),多組模型(multiple groups),增長曲線模型(growth curve models),中介分析(mediation analysis),分類數據(categorial data)等。
1. 在開始之前
在開始之前,有以下幾點需要註意:
- lavaan包需要安裝 3.0.0或更新版本的R。
- lavaan包仍處於未完成階段,目前尚未實現的功能有:對多層數據的支持,對離散潛變數的支持,貝葉斯估計。
- 雖然目前是測試版,但是結果精確,語法成熟,可以放心使用。
- lavaan包對R語言預備知識要求很低。
- 此教程不等於參考手冊,相關文檔正在準備。
- lavaan包是完全免費開源的軟體,不做任何承諾。
- 發現bug,到 https://groups.google.com/d/forum/lavaan/ 加組溝通。
2. 安裝lavaan包
啟動R,並輸入:
install.packages("lavaan", dependencies = TRUE) # 安裝lavaan包
library(lavaan) # 載入lavaan包出現以下提示,表示載入成功。

3. 模型語法
lavaan包的核心是描述整個模型的“模型語法”。這部分簡單介紹語法,更多細節在接下來的示例中可見。
R環境下的回歸方程有如下形式:
y ~ x1 + x2 + x3 + x4 # ~左邊為因變數y在lavaan中,一個典型模型是一個回歸方程組,其中可以包含潛變數,例如:
y ~ f1 + f2 + x1 + x2
f1 ~ f2 + f3
f2 ~ f3 + x1 + x2我們必須通過指示符=~(measured by)來“定義”潛變數。例如,通過以下方式來定義潛變數f1, f2和f3:
f1 =~ y1 + y2 + y3
f2 =~ y4 + y5 + y6
f3 =~ y7 + y8 + y9 + y10方差和協方差表示如下:
y1 ~~ y1 # 方差
y1 ~~ y2 # 協方差
f1 ~~ f2 # 協方差只有截距項的回歸方程表達如下:
y1 ~ 1
f1 ~ 1以上4種公式種類(~, ~~, =~, ~ 1)組合成完整的模型語法,用單引號表示如下:
myModel <- ' # 主要回歸方程
y1 + y2 ~ f1 + f2 + x1 + x2
f1 ~ f2 + f3
f2 ~ f3 + x1 + x2
# 定義潛變數
f1 =~ y1 + y2 + y3
f2 =~ y4 + y5 + y6
f3 =~ y7 + y8 + y9 + y10
# 方差和協方差
y1 ~~ y1
y1 ~~ y2
f1 ~~ f2
# 截距項
y1 ~ 1
f1 ~ 1如果模型很長,可以將模型(單引號之間的內容)儲存入myModel.lav的txt文檔中,用以下命令讀取:
myModel <- readLines("/mydirectory/myModel.lav") # 這裡需要絕對路徑4. 例1:驗證性因數分析(CFA)
lavaan包提供了一個內置數據集叫做HolzingerSwineford,輸入以下命令查看數據集描述:
?HolzingerSwineford數據形式是這樣的:

此數據集包含了來自兩個學校的七、八年級孩子的智力能力測驗分數。在我們的版本里,只包含原有26個測試中的9個,這9個測試分數作為9個測量變數分別對應3個潛變數:
- 視覺因數(visual)對應x1,x2,x3
- 文本因數(textual)對應x4,x5,x6
- 速度因數(speed)對應x7,x8,x9
模型如下圖所示:
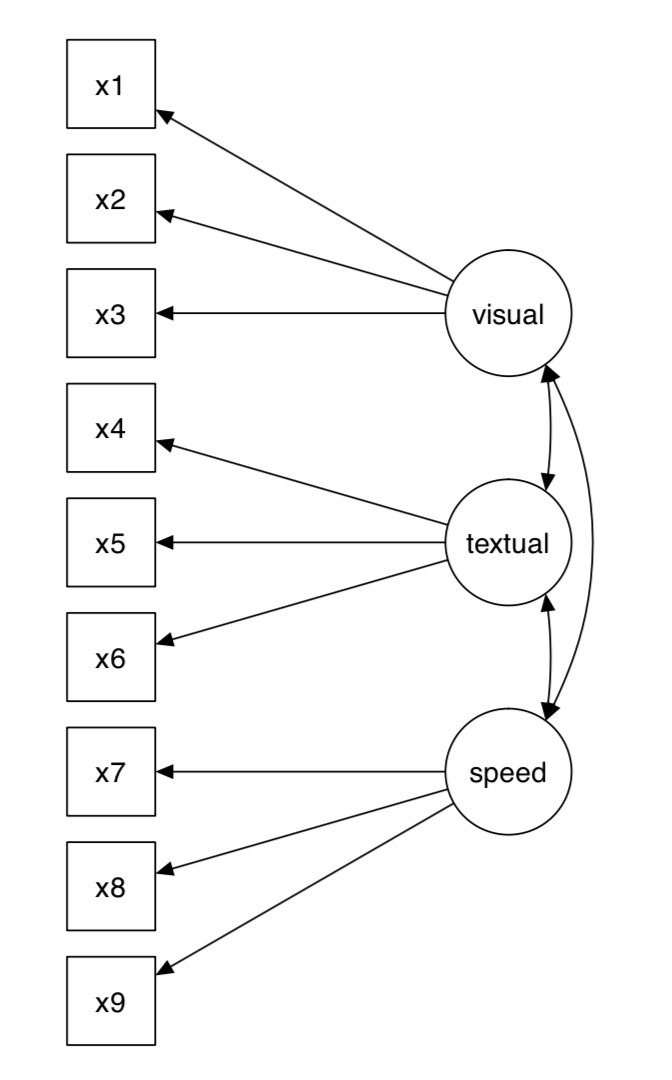
建立模型代碼如下:
HS.model <- ' visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9'
# 然後擬合cfa函數,第一個參數是模型,第二個參數是數據集
fit <- cfa(HS.model, data = HolzingerSwineford1939)
# 再通過summary函數給出結果
summary(fit, fit.measure = TRUE)結果展示如下:
# 前6行為頭部,包含版本號,收斂情況,迭代次數,觀測數,用來計算參數的估計量,模型檢驗統計量,自由度和相關的p值
lavaan (0.5-23.1097) converged normally after 35 iterations
Number of observations 301
Estimator ML
Minimum Function Test Statistic 85.306
Degrees of freedom 24
P-value (Chi-square) 0.000
#參數fit.measure = TRUE會顯示下麵從model test baseline model到SRMR的部分
Model test baseline model:
Minimum Function Test Statistic 918.852
Degrees of freedom 36
P-value 0.000
User model versus baseline model:
Comparative Fit Index (CFI) 0.931
Tucker-Lewis Index (TLI) 0.896
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -3737.745
Loglikelihood unrestricted model (H1) -3695.092
Number of free parameters 21
Akaike (AIC) 7517.490
Bayesian (BIC) 7595.339
Sample-size adjusted Bayesian (BIC) 7528.739
Root Mean Square Error of Approximation:
RMSEA 0.092
90 Percent Confidence Interval 0.071 0.114
P-value RMSEA <= 0.05 0.001
Standardized Root Mean Square Residual:
SRMR 0.065
#以下是參數估計部分
Parameter Estimates:
Information Expected
Standard Errors Standard
Latent Variables:
Estimate Std.Err z-value P(>|z|)
visual =~
x1 1.000
x2 0.554 0.100 5.554 0.000
x3 0.729 0.109 6.685 0.000
textual =~
x4 1.000
x5 1.113 0.065 17.014 0.000
x6 0.926 0.055 16.703 0.000
speed =~
x7 1.000
x8 1.180 0.165 7.152 0.000
x9 1.082 0.151 7.155 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
visual ~~
textual 0.408 0.074 5.552 0.000
speed 0.262 0.056 4.660 0.000
textual ~~
speed 0.173 0.049 3.518 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.x1 0.549 0.114 4.833 0.000
.x2 1.134 0.102 11.146 0.000
.x3 0.844 0.091 9.317 0.000
.x4 0.371 0.048 7.779 0.000
.x5 0.446 0.058 7.642 0.000
.x6 0.356 0.043 8.277 0.000
.x7 0.799 0.081 9.823 0.000
.x8 0.488 0.074 6.573 0.000
.x9 0.566 0.071 8.003 0.000
visual 0.809 0.145 5.564 0.000
textual 0.979 0.112 8.737 0.000
speed 0.384 0.086 4.451 0.000例1是一個定義模型、擬合模型、提取結果的過程。
5. 例2:結構方程(SEM)
例2中我們使用名為PoliticalDemocracy的數據集,圖示如下:
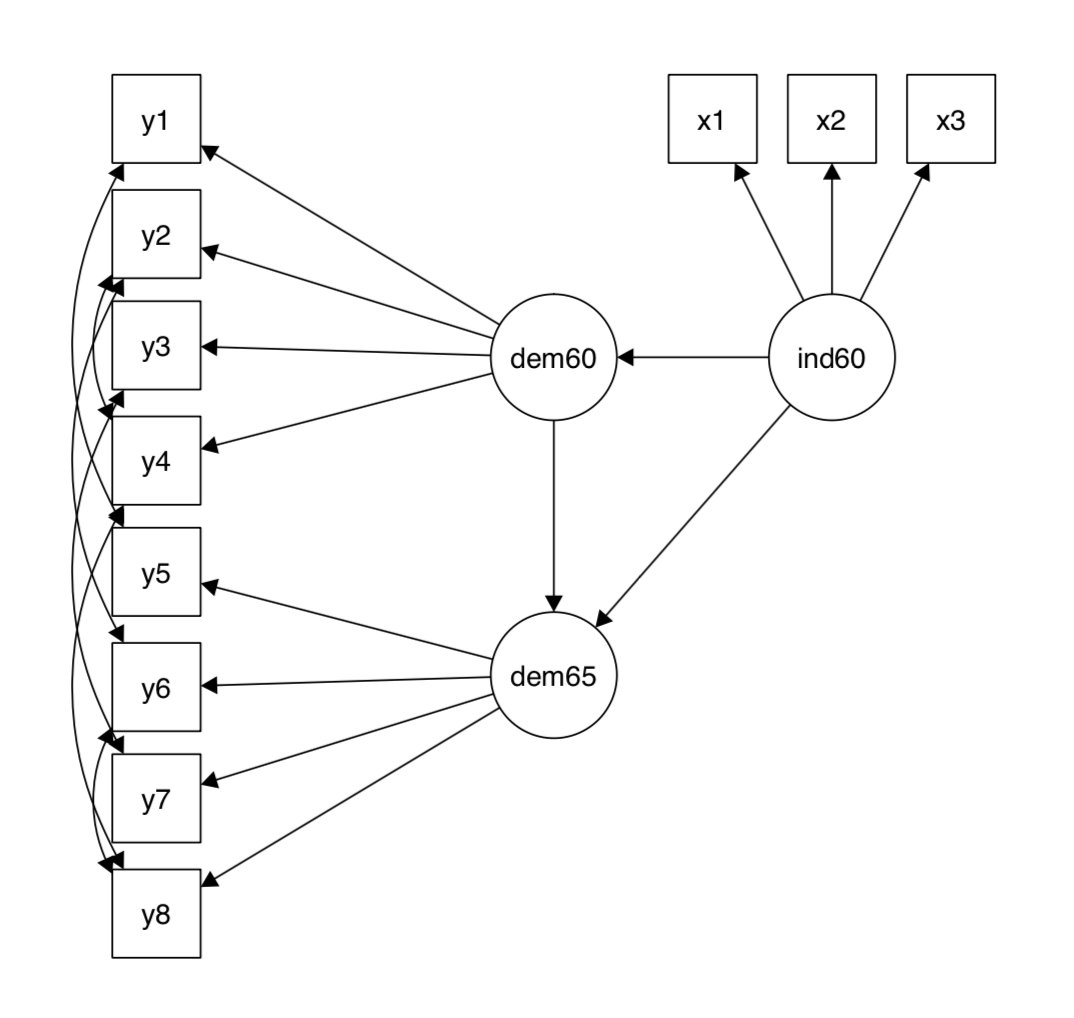
數據形式大致如下(只顯示前三行):

| 變數 | 含義 | 變數 | 含義 |
|---|---|---|---|
| ind60 | 1960年的非民主情況 | y5 | 1965年專家對出版物自由的評價 |
| dem60 | 1960年的民主情況 | y6 | 1965年的反對黨派自由 |
| dem65 | 1965年的民主情況 | y7 | 1965年選舉的公平性 |
| y1 | 1960年專家對出版物自由的評價 | y8 | 1965年選舉產生的立法機關效率 |
| y2 | 1960年的反對黨派自由 | x1 | 1960年每單位資本GNP |
| y3 | 1960年選舉的公平性 | x2 | 1960年每單位資本的物質能量消費 |
| y4 | 1960年選舉產生的立法機關效率 | x3 | 1960年工業勞動力占比 |
模型如下:
model <- '# measurement model 測量模型
ind60 =~ x1 + x2 + x3
dem60 =~ y1 + y2 + y3 + y4
dem65 =~ y5 + y6 + y7 + y8
# regressions 回歸
dem60 ~ ind60
dem65 ~ ind60 + dem60
# residual correlations 殘餘相關
y1 ~~ y5
y2 ~~ y4 + y6
y3 ~~ y7
y4 ~~ y8
y6 ~~ y8'
# 擬合SEM
fit <- sem(model, data = PoliticalDemocracy)
# 提取結果
summary(fit, standardized = TRUE)
#與上例不同,這裡我們忽略了參數fit.measure = TRUE,用standardized = TRUE來標準化參數值)結果如下:
lavaan (0.5-23.1097) converged normally after 68 iterations
Number of observations 75
Estimator ML
Minimum Function Test Statistic 38.125
Degrees of freedom 35
P-value (Chi-square) 0.329
Parameter Estimates:
Information Expected
Standard Errors Standard
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
ind60 =~
x1 1.000 0.670 0.920
x2 2.180 0.139 15.742 0.000 1.460 0.973
x3 1.819 0.152 11.967 0.000 1.218 0.872
dem60 =~
y1 1.000 2.223 0.850
y2 1.257 0.182 6.889 0.000 2.794 0.717
y3 1.058 0.151 6.987 0.000 2.351 0.722
y4 1.265 0.145 8.722 0.000 2.812 0.846
dem65 =~
y5 1.000 2.103 0.808
y6 1.186 0.169 7.024 0.000 2.493 0.746
y7 1.280 0.160 8.002 0.000 2.691 0.824
y8 1.266 0.158 8.007 0.000 2.662 0.828
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
dem60 ~
ind60 1.483 0.399 3.715 0.000 0.447 0.447
dem65 ~
ind60 0.572 0.221 2.586 0.010 0.182 0.182
dem60 0.837 0.098 8.514 0.000 0.885 0.885
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.y1 ~~
.y5 0.624 0.358 1.741 0.082 0.624 0.296
.y2 ~~
.y4 1.313 0.702 1.871 0.061 1.313 0.273
.y6 2.153 0.734 2.934 0.003 2.153 0.356
.y3 ~~
.y7 0.795 0.608 1.308 0.191 0.795 0.191
.y4 ~~
.y8 0.348 0.442 0.787 0.431 0.348 0.109
.y6 ~~
.y8 1.356 0.568 2.386 0.017 1.356 0.338
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.x1 0.082 0.019 4.184 0.000 0.082 0.154
.x2 0.120 0.070 1.718 0.086 0.120 0.053
.x3 0.467 0.090 5.177 0.000 0.467 0.239
.y1 1.891 0.444 4.256 0.000 1.891 0.277
.y2 7.373 1.374 5.366 0.000 7.373 0.486
.y3 5.067 0.952 5.324 0.000 5.067 0.478
.y4 3.148 0.739 4.261 0.000 3.148 0.285
.y5 2.351 0.480 4.895 0.000 2.351 0.347
.y6 4.954 0.914 5.419 0.000 4.954 0.443
.y7 3.431 0.713 4.814 0.000 3.431 0.322
.y8 3.254 0.695 4.685 0.000 3.254 0.315
ind60 0.448 0.087 5.173 0.000 1.000 1.000
.dem60 3.956 0.921 4.295 0.000 0.800 0.800
.dem65 0.172 0.215 0.803 0.422 0.039 0.039可以看出sem()和cfa()這兩個函數很相似,實際上,這兩個函數現在幾乎是一樣的,但在將來可能發生變化。
在添加了standardized參數後,出現了Std.lv, Std.all兩列,前者只有潛變數被標準化了,後者為所有變數都標準化了,也被稱為“完全標準化解”。
6. 更多關於語法的內容
6.1 固定參數
對於一個對應4個指標的潛變數,lavaan預設將第一個指標的因數載荷固定為1,其他指標為自由。
但如果你有一個很好的理由來讓所有因數載荷都固定為1,可以照如下做法:
f =~ y1 + 1*y2 + 1*y3 + 1*y4一般來說,你需要通過給相關變數預先乘以一個數字來固定公式的參數,這個叫做“預乘機制”。
回想例1中的模型,預設3個潛變數兩兩相關。如果你想將某對變數的相關係數設為0,你需要為其添加一個協方差公式並將參數設為0.
在下麵的語法中,除visual,textual間的協方差自由外,其他均設為0。並且我們希望固定speed的因數為一個單位,所以不需要設定第一個指標x7為1,因此我們給x7乘以NA使x7的因數載荷自由且未知,整個模型如下:
# three-factor model
visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ NA*x7 + x8 + x9
# orthogonal factors 正交因數
visual ~~ 0*speed
textual ~~ 0*speed
# fix variance of speed factor
speed ~~ 1*speed 你也可以用orthogonal = TRUE參數使所有潛變數正交,操作如下:
HS.model <- 'visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9'
fit.HS.ortho <- cfa(HS.model, data = HolzingerSwineford1939, orthogonal = TRUE)相似的,你可以用std.lv = TRUE使所有潛變數的方差固定為一個單位:
HS.model <- 'visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9'
fit <- cfa(HS.model, data = HolzingerSwineford1939, std.lv = TRUE)6.2 初值
lavaan包預設為自由參數自動生成初值,你也可以通過start()函數來自己設定初值,示例如下:
visual =~ x1 + start(0.8)*x2 + start(1.2)*x3
textual =~ x4 + start(0.5)x5 + start(1.0)x6
speed =~ x7 + start(0.7)x8 + start(1.8)x96.3 參數標簽
我們也可以自己定義參數標簽,標簽不能以數字開頭:
model <- '
# latent variable definitions
ind60 =~ x1 + x2 + myLabel*x3 #將ind60 =~ x3顯示為myLabel
dem60 =~ y1 + y2 + y3 + y4
dem65 =~ y5 + y6 + y7 + y8
# regressions
dem60 ~ ind60
dem65 ~ ind60 + dem60
# residual (co)variances
y1 ~~ y5
y2 ~~ y4 + y6
y3 ~~ y7
y4 ~~ y8
y6 ~~ y8'
fit <- sem(model,
data = PoliticalDemocracy)
coef(fit)結果如下:

6.4 修改器
我們預乘機制所使用的固定參數,修改初始值和參數標簽等操作,都可以稱為修改器,比如:
f =~ y1 + y2 + myLabel*y3 + start(0.5)*y3 + y4
#雖然y3項出現了兩次,過濾器仍然會將y3作為一個指標對待6.5 簡單相等約束
有些情況我們會預設變數參數相等,可以用相同的label達到效果,也可以用equal()函數:
visual =~ x1 + v2*x2 + v2*x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9
#或者用equal()
visual =~ x1 + x2 + equal("visual=~x2")*x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x96.6 非線性相等和不相等約束
假設有如下回歸方程:
y ~ b1*x1 + b2*x2 + b3*x3我們用隨機數生成一個數據集,並用sem函數擬合:
set.seed(1234)
Data <- data.frame(y = rnorm(100),
x1 = rnorm(100),
x2 = rnorm(100),
x3 = rnorm(100))
model <- 'y ~ b1*x1 + b2*x2 + b3*x3'
fit <- sem(model, data = Data)
coef(fit)結果為:
b1 b2 b3 y~~y
-0.052 0.084 0.139 0.970
如果我們想要為b1增加兩個約束:\(b_1=(b_2+b_3)^2\) 和 \(b_1\ge\exp(b_2+b_3)\),操作如下:
model.constr <- '# model with labeled parameters
y ~ b1*x1 + b2*x2 + b3*x3
# constraints
b1 == (b2 + b3)^2
b1 > exp(b2 + b3)'
fit <- sem(model.constr, data = Data)
coef(fit)結果如下:
b1 b2 b3 y~~y
0.495 -0.405 -0.299 1.6107. 引入平均值
總的來說,結構方程用來模擬指標變數的協方差矩陣,但是在一些應用中,引入指標變數的均值也是有用的。一個方法是求助於截距項,使用如下所示的“截距公式”:
variable ~ 1右邊的1代表截距,比如在例1中,我們可以增加截距項到指標變數中:
# three-factor model
visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9
# intercepts
x1 ~ 1
x2 ~ 1
x3 ~ 1
x4 ~ 1
x5 ~ 1
x6 ~ 1
x7 ~ 1
x8 ~ 1
x9 ~ 1然而還有一種更簡單的方法:
fit <- cfa(HS.model,
data = HolzingerSwineford1939,
meanstructure = TRUE)
summary(fit)結果如下:
lavaan (0.5-23.1097) converged normally after 35 iterations
Number of observations 301
Estimator ML
Minimum Function Test Statistic 85.306
Degrees of freedom 24
P-value (Chi-square) 0.000
Parameter Estimates:
Information Expected
Standard Errors Standard
Latent Variables:
Estimate Std.Err z-value P(>|z|)
visual =~
x1 1.000
x2 0.554 0.100 5.554 0.000
x3 0.729 0.109 6.685 0.000
textual =~
x4 1.000
x5 1.113 0.065 17.014 0.000
x6 0.926 0.055 16.703 0.000
speed =~
x7 1.000
x8 1.180 0.165 7.152 0.000
x9 1.082 0.151 7.155 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
visual ~~
textual 0.408 0.074 5.552 0.000
speed 0.262 0.056 4.660 0.000
textual ~~
speed 0.173 0.049 3.518 0.000
Intercepts:
Estimate Std.Err z-value P(>|z|)
.x1 4.936 0.067 73.473 0.000
.x2 6.088 0.068 89.855 0.000
.x3 2.250 0.065 34.579 0.000
.x4 3.061 0.067 45.694 0.000
.x5 4.341 0.074 58.452 0.000
.x6 2.186 0.063 34.667 0.000
.x7 4.186 0.063 66.766 0.000
.x8 5.527 0.058 94.854 0.000
.x9 5.374 0.058 92.546 0.000
visual 0.000
textual 0.000
speed 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.x1 0.549 0.114 4.833 0.000
.x2 1.134 0.102 11.146 0.000
.x3 0.844 0.091 9.317 0.000
.x4 0.371 0.048 7.779 0.000
.x5 0.446 0.058 7.642 0.000
.x6 0.356 0.043 8.277 0.000
.x7 0.799 0.081 9.823 0.000
.x8 0.488 0.074 6.573 0.000
.x9 0.566 0.071 8.003 0.000
visual 0.809 0.145 5.564 0.000
textual 0.979 0.112 8.737 0.000
speed 0.384 0.086 4.451 0.000如上圖所示,模型包含觀測變數和潛變數的截距參數。lavaan包預設cfa()和sem()函數將潛變數截距固定為0,否則模型不能被估計。要註意的是均值結構模型中卡方統計量和自由度和原方程一樣,原因是我們引入了9個觀測變數的均值,也同時加上了9個額外的結截距參數。新老兩模型的估計結果是完全一樣的。在實踐中,我們增加截距公式的唯一原因是因為一些約束必須被規定。例如,我們必須設定x1,x2,x3,x4的截距都為0.5時,語法如下:
# three-factor model
visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9
# intercepts with fixed values
x1 + x2 + x3 + x4 ~ 0.5*18. 結構方程的多組分析
lavaan包完全支持多組分析。為了進行多組分析,你需要在數據組中加上組變數的名稱。預設情況下,所有組會擬合相同的模型。在以下示例中,我們針對兩個學校(Pasteur和Grant-White,可以看到數據集中有關學校的變數名為school)擬合例1的模型:
HS.model <- 'visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9'
fit <- cfa(HS.model,
data = HolzingerSwineford1939,
group = "school")
summary(fit)結果如下:
lavaan (0.5-23.1097) converged normally after 57 iterations
Number of observations per group
Pasteur 156
Grant-White 145
Estimator ML
Minimum Function Test Statistic 115.851
Degrees of freedom 48
P-value (Chi-square) 0.000
Chi-square for each group:
Pasteur 64.309
Grant-White 51.542
Parameter Estimates:
Information Expected
Standard Errors Standard
Group 1 [Pasteur]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
visual =~
x1 1.000
x2 0.394 0.122 3.220 0.001
x3 0.570 0.140 4.076 0.000
textual =~
x4 1.000
x5 1.183 0.102 11.613 0.000
x6 0.875 0.077 11.421 0.000
speed =~
x7 1.000
x8 1.125 0.277 4.057 0.000
x9 0.922 0.225 4.104 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
visual ~~
textual 0.479 0.106 4.531 0.000
speed 0.185 0.077 2.397 0.017
textual ~~
speed 0.182 0.069 2.628 0.009
Intercepts:
Estimate Std.Err z-value P(>|z|)
.x1 4.941 0.095 52.249 0.000
.x2 5.984 0.098 60.949 0.000
.x3 2.487 0.093 26.778 0.000
.x4 2.823 0.092 30.689 0.000
.x5 3.995 0.105 38.183 0.000
.x6 1.922 0.079 24.321 0.000
.x7 4.432 0.087 51.181 0.000
.x8 5.563 0.078 71.214 0.000
.x9 5.418 0.079 68.440 0.000
visual 0.000
textual 0.000
speed 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.x1 0.298 0.232 1.286 0.198
.x2 1.334 0.158 8.464 0.000
.x3 0.989 0.136 7.271 0.000
.x4 0.425 0.069 6.138 0.000
.x5 0.456 0.086 5.292 0.000
.x6 0.290 0.050 5.780 0.000
.x7 0.820 0.125 6.580 0.000
.x8 0.510 0.116 4.406 0.000
.x9 0.680 0.104 6.516 0.000
visual 1.097 0.276 3.967 0.000
textual 0.894 0.150 5.963 0.000
speed 0.350 0.126 2.778 0.005
Group 2 [Grant-White]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
visual =~
x1 1.000
x2 0.736 0.155 4.760 0.000
x3 0.925 0.166 5.583 0.000
textual =~
x4 1.000
x5 0.990 0.087 11.418 0.000
x6 0.963 0.085 11.377 0.000
speed =~
x7 1.000
x8 1.226 0.187 6.569 0.000
x9 1.058 0.165 6.429 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
visual ~~
textual 0.408 0.098 4.153 0.000
speed 0.276 0.076 3.639 0.000
textual ~~
speed 0.222 0.073 3.022 0.003
Intercepts:
Estimate Std.Err z-value P(>|z|)
.x1 4.930 0.095 51.696 0.000
.x2 6.200 0.092 67.416 0.000
.x3 1.996 0.086 23.195 0.000
.x4 3.317 0.093 35.625 0.000
.x5 4.712 0.096 48.986 0.000
.x6 2.469 0.094 26.277 0.000
.x7 3.921 0.086 45.819 0.000
.x8 5.488 0.087 63.174 0.000
.x9 5.327 0.085 62.571 0.000
visual 0.000
textual 0.000
speed 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.x1 0.715 0.126 5.676 0.000
.x2 0.899 0.123 7.339 0.000
.x3 0.557 0.103 5.409 0.000
.x4 0.315 0.065 4.870 0.000
.x5 0.419 0.072 5.812 0.000
.x6 0.406 0.069 5.880 0.000
.x7 0.600 0.091 6.584 0.000
.x8 0.401 0.094 4.249 0.000
.x9 0.535 0.089 6.010 0.000
visual 0.604 0.160 3.762 0.000
textual 0.942 0.152 6.177 0.000
speed 0.461 0.118 3.910 0.000如果你想要固定參數,或者自己設定初值,只需要用到如下所示的參數數列。如果只用一個參數的話,這個參數會被用到所有組:
HS.model <- 'visual =~ x1 + 0.5*x2 + c(0.6, 0.8)*x3
textual =~ x4 + start(c(1.2, 0.6))*x5 + a*x6
speed =~ x7 + x8 + x9'註意如上所示的a只會被用於第一組,如果想為每組提供不同的標簽,可以使用c(a1, a2)*x6,要註意不能使用c(a, a), 它們會被視為一個相同的參數,使得結果出現問題(請看8.2,這會導致兩組中textual =~ x6的估計相等)。
8.1 在部分組中固定參數
操作如下:
f =~ item1 + c(1,NA,1,1)*item2 + item38.2 約束一個參數使其在各組中相等
操作如下:
HS.model <- 'visual =~ x1 + x2 + c(v3,v3)*x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9'8.3 約束一組參數使其在各組中相等
一個更方便的辦法,通過group.equal()來做“組間相等約束”。例如,約束所有因數載荷使其在各組中相等(觀測變數對潛變數在各組中的對應繫數都相等,即latent variables中的estimate):
HS.model <- 'visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9'
fit <- cfa(HS.model,
data = HolzingerSwineford1939,
group = "school",
group.equal = c("loadings"))
summary(fit)結果如下:
lavaan (0.5-23.1097) converged normally after 42 iterations
Number of observations per group
Pasteur 156
Grant-White 145
Estimator ML
Minimum Function Test Statistic 124.044
Degrees of freedom 54
P-value (Chi-square) 0.000
Chi-square for each group:
Pasteur 68.825
Grant-White 55.219
Parameter Estimates:
Information Expected
Standard Errors Standard
Group 1 [Pasteur]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
visual =~
x1 1.000
x2 (.p2.) 0.599 0.100 5.979 0.000
x3 (.p3.) 0.784 0.108 7.267 0.000
textual =~
x4 1.000
x5 (.p5.) 1.083 0.067 16.049 0.000
x6 (.p6.) 0.912 0.058 15.785 0.000
speed =~
x7 1.000
x8 (.p8.) 1.201 0.155 7.738 0.000
x9 (.p9.) 1.038 0.136 7.629 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
visual ~~
textual 0.416 0.097 4.271 0.000
speed 0.169 0.064 2.643 0.008
textual ~~
speed 0.176 0.061 2.882 0.004
Intercepts:
Estimate Std.Err z-value P(>|z|)
.x1 4.941 0.093 52.991 0.000
.x2 5.984 0.100 60.096 0.000
.x3 2.487 0.094 26.465 0.000
.x4 2.823 0.093 30.371 0.000
.x5 3.995 0.101 39.714 0.000
.x6 1.922 0.081 23.711 0.000
.x7 4.432 0.086 51.540 0.000
.x8 5.563 0.078 71.087 0.000
.x9 5.418 0.079 68.153 0.000
visual 0.000
textual 0.000
speed 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.x1 0.551 0.137 4.010 0.000
.x2 1.258 0.155 8.117 0.000
.x3 0.882 0.128 6.884 0.000
.x4 0.434 0.070 6.238 0.000
.x5 0.508 0.082 6.229 0.000
.x6 0.266 0.050 5.294 0.000
.x7 0.849 0.114 7.468 0.000
.x8 0.515 0.095 5.409 0.000
.x9 0.658 0.096 6.865 0.000
visual 0.805 0.171 4.714 0.000
textual 0.913 0.137 6.651 0.000
speed 0.305 0.078 3.920 0.000
Group 2 [Grant-White]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
visual =~
x1 1.000
x2 (.p2.) 0.599 0.100 5.979 0.000
x3 (.p3.) 0.784 0.108 7.267 0.000
textual =~
x4 1.000
x5 (.p5.) 1.083 0.067 16.049 0.000
x6 (.p6.) 0.912 0.058 15.785 0.000
speed =~
x7 1.000
x8 (.p8.) 1.201 0.155 7.738 0.000
x9 (.p9.) 1.038 0.136 7.629 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
visual ~~
textual 0.437 0.099 4.423 0.000
speed 0.314 0.079 3.958 0.000
textual ~~
speed 0.226 0.072 3.144 0.002
Intercepts:
Estimate Std.Err z-value P(>|z|)
.x1 4.930 0.097 50.763 0.000
.x2 6.200 0.091 68.379 0.000
.x3 1.996 0.085 23.455 0.000
.x4 3.317 0.092 35.950 0.000
.x5 4.712 0.100 47.173 0.000
.x6 2.469 0.091 27.248 0.000
.x7 3.921 0.086 45.555 0.000
.x8 5.488 0.087 63.257 0.000
.x9 5.327 0.085 62.786 0.000
visual 0.000
textual 0.000
speed 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.x1 0.645 0.127 5.084 0.000
.x2 0.933 0.121 7.732 0.000
.x3 0.605 0.096 6.282 0.000
.x4 0.329 0.062 5.279 0.000
.x5 0.384 0.073 5.270 0.000
.x6 0.437 0.067 6.576 0.000
.x7 0.599 0.090 6.651 0.000
.x8 0.406 0.089 4.541 0.000
.x9 0.532 0.086 6.202 0.000
visual 0.722 0.161 4.490 0.000
textual 0.906 0.136 6.646 0.000
speed 0.475 0.109 4.347 0.000group.equal()的其他的參數就不翻譯了,太累。
- intercepts: the intercepts of the observed variables
- means: the intercepts/means of the latent variables
- residuals: the residual variances of the observed variables
- residual.covariances: the residual covariances of the observed variables
- lv.variances: the (residual) variances of the latent variables
- lv.covariances: the (residual) covariances of the latent varibles
- regressions: all regression coefficients in the model
8.4 測量不變性
因數分析的測量不變性(Measurement Invariance)是指測驗的觀察變數與潛變數之間的關係在不同組別或時間點上保持不變。測量不變性的成立是進行有意義組間比較的重要前提。可以用semTools包的measurementInvariance()函數來按特定次序執行多組分析,每個模型都與基線模型比較並且對先前的模型進行卡方差異性檢驗,並且展示擬合度量差別。不過這個方法仍舊比較原始。
library(semTools)
measurementInvariance(HS.model,
data = HolzingerSwineford1939,
group = "school")9. 增長曲線模型
潛變數模型的另一個重要種類是潛增長曲線模型。增長模型常用於分析縱向和發展數據。這種數據的結果度量基於幾個場景,我們需要研究跨時間變化。在許多情況下,隨時間變化的軌跡可以用簡單線性或二次函數曲線來模擬。隨機效應用來捕捉個體間差異,這種隨機效應可以很方便地用潛變數表示,也叫做增長因數。
在以下例子中,我們使用人工數據Demo.growth(),包含4個時間點。為了在4個時間點上擬合線性增長模型,我們需要用到含有一個隨機截距潛變數和一個隨機斜率潛變數的模型。
模型如下:
# linear growth model with 4 timepoints
# intercept and slope with fixed coefficients
i =~ 1*t1 + 1*t2 + 1*t3 + 1*t4
s =~ 0*t1 + 1*t2 + 2*t3 + 3*t4
數據格式如下:

代碼如下:
model <- 'i =~ 1*t1 + 1*t2 + 1*t3 + 1*t4
s =~ 0*t1 + 1*t2 + 2*t3 + 3*t4'
fit <- growth(model, data = Demo.growth)
summary(fit)結果如下:
lavaan (0.5-23.1097) converged normally after 29 iterations
Number of observations 400
Estimator ML
Minimum Function Test Statistic 8.069
Degrees of freedom 5
P-value (Chi-square) 0.152
Parameter Estimates:
Information Expected
Standard Errors Standard
Latent Variables:
Estimate Std.Err z-value P(>|z|)
i =~
t1 1.000
t2 1.000
t3 1.000
t4 1.000
s =~
t1 0.000
t2 1.000
t3 2.000
t4 3.000
Covariances:
Estimate Std.Err z-value P(>|z|)
i ~~
s 0.618 0.071 8.686 0.000
Intercepts:
Estimate Std.Err z-value P(>|z|)
.t1 0.000
.t2 0.000
.t3 0.000
.t4 0.000
i 0.615 0.077 8.007 0.000
s 1.006 0.042 24.076 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.t1 0.595 0.086 6.944 0.000
.t2 0.676 0.061 11.061 0.000
.t3 0.635 0.072 8.761 0.000
.t4 0.508 0.124 4.090 0.000
i 1.932 0.173 11.194 0.000
s 0.587 0.052 11.336 0.000從技巧上來看,growth()函數與sem()幾乎相同。但是其自動包含了均值結構假設,並預設觀測截距固定為0,潛變數結局和均值自由估計。現在我們再加入兩個變數x1,x2,發展出以下模型:

代碼如下:
# a linear growth model with a time-varying covariate
model <- '# intercept and slope with fixed coefficients
i =~ 1*t1 + 1*t2 + 1*t3 + 1*t4
s =~ 0*t1 + 1*t2 + 2*t3 + 3*t4
# regressions
i ~ x1 + x2
s ~ x1 + x2
# time-varying covariates
t1 ~ c1
t2 ~ c2
t3 ~ c3
t4 ~ c4'
fit <- growth(model, data = Demo.growth)
summary(fit)10. 使用分類變數
對於外生分類變數:直接轉換成虛擬變數。
對於內生分類變數:可以直接處理,目前只有WLS方法可用。
fit <- cfa(myModel, data = myData,
ordered=c("item1","item2",
"item3","item4"))11. 將協方差矩陣作為輸入
在沒有完整數據集但有協方差矩陣時可以使用,如下例:
# 輸入協方差矩陣
lower <- '
11.834
6.947 9.364
6.819 5.091 12.532
4.783 5.028 7.495 9.986
-3.839 -3.889 -3.841 -3.625 9.610
-21.899 -18.831 -21.748 -18.775 35.522 450.288'
# 用getCov建立完整協方差矩陣,輸出是一個矩陣
wheaton.cov <-
getCov(lower, names = c("anomia67", "powerless67",
"anomia71", "powerless71",
"education", "sei"))
# 模型描述
wheaton.model <- '
# latent variables
ses =~ education + sei
alien67 =~ anomia67 + powerless67
alien71 =~ anomia71 + powerless71
# regressions
alien71 ~ alien67 + ses
alien67 ~ ses
# correlated residuals
anomia67 ~~ anomia71
powerless67 ~~ powerless71'
fit <- sem(wheaton.model,
sample.cov = wheaton.cov,
sample.nobs = 932)
summary(fit, standardized = TRUE)結果如下:
lavaan (0.5-23.1097) converged normally after 73 iterations
Number of observations 932
Estimator ML
Minimum Function Test Statistic 4.735
Degrees of freedom 4
P-value (Chi-square) 0.316
Parameter Estimates:
Information Expected
Standard Errors Standard
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
ses =~
education 1.000 2.607 0.842
sei 5.219 0.422 12.364 0.000 13.609 0.642
alien67 =~
anomia67 1.000 2.663 0.774
powerless67 0.979 0.062 15.895 0.000 2.606 0.852
alien71 =~
anomia71 1.000 2.850 0.805
powerless71 0.922 0.059 15.498 0.000 2.628 0.832
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
alien71 ~
alien67 0.607 0.051 11.898 0.000 0.567 0.567
ses -0.227 0.052 -4.334 0.000 -0.207 -0.207
alien67 ~
ses -0.575 0.056 -10.195 0.000 -0.563 -0.563
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.anomia67 ~~
.anomia71 1.623 0.314 5.176 0.000 1.623 0.356
.powerless67 ~~
.powerless71 0.339 0.261 1.298 0.194 0.339 0.121
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.education 2.801 0.507 5.525 0.000 2.801 0.292
.sei 264.597 18.126 14.597 0.000 264.597 0.588
.anomia67 4.731 0.453 10.441 0.000 4.731 0.400
.powerless67 2.563 0.403 6.359 0.000 2.563 0.274
.anomia71 4.399 0.515 8.542 0.000 4.399 0.351
.powerless71 3.070 0.434 7.070 0.000 3.070 0.308
ses 6.798 0.649 10.475 0.000 1.000 1.000
.alien67 4.841 0.467 10.359 0.000 0.683 0.683
.alien71 4.083 0.404 10.104 0.000 0.503 0.503
12. 估計方法,標準誤差和缺失值
12.1 估計方法
如果所有數據都是連續的,預設估計方法是最大似然法,還有一些其他方法:
- "GLS": generalized least squares. 只能用於完整數據
- "WLS": weighted least squares (sometimes called ADF estimation). 只能用於完整數據
- "DWLS": diagonally weighted least squares
- "ULS": unweighted least squares
許多估計方法都有“穩健”變體,意味著它們提供穩健標準誤差和縮放的檢驗統計量。例如,對於最大似然,lavaan提供如下穩健變體:
- "MLM": maximum likelihood estimation with robust standard errors and a Satorra-Bentler scaled test statistic. 只能用於完整數據
- "MLMVS": maximum likelihood estimation with robust standard errors and a mean- and variance adjusted test statistic (aka the Satterthwaite approach). 只能用於完整數據
- "MLMV": maximum likelihood estimation with robust standard errors and a mean- and variance adjusted test statistic (using a scale-shifted approach). 只能用於完整數據
- "MLF": for maximum likelihood estimation with standard errors based on the first-order derivatives, and a conventional test statistic. 可以用於完整和非完整數據
- "MLR": maximum likelihood estimation with robust (Huber-White) standard errors and a scaled test statistic that is (asymptotically) equal to the Yuan-Bentler test statistic. 可以用於完整和非完整數據
12.2 最大似然估計
lavaan預設使用有偏樣本協方差矩陣,與Mplus所使用方法相似(“normal”)。我們也可以使用likelihood = "wishart"來使用無偏協方差用以接近EQS, LISREL或AMOS的計算結果(“Wishart”):
fit <- cfa(HS.model,
data = HolzingerSwineford1939,
fit12.3 缺失值
預設為列表狀態刪除,在進行統計量的計算時,把含有缺失值的記錄刪除,這種方法可以用於計算全體無缺失值數據的均數、協方差和標準差。
13. 間接效應和中介分析
設想一個典型的中介分析,X->M->Y,隨機生成人工數據,示例如下:
set.seed(1234)
X <- rnorm(100)
M <- 0.5*X + rnorm(100)
Y <- 0.7*M + rnorm(100)
Data <- data.frame(X = X, Y = Y, M = M)
model <- '# direct effect
Y ~ c*X
# mediator
M ~ a*X
Y ~ b*M
# indirect effect (a*b)
ab := a*b
# total effect
total := c + (a*b)'
fit <- sem(model, data = Data)
summary(fit)結果如下:
lavaan (0.5-23.1097) converged normally after 12 iterations
Number of observations 100
Estimator ML
Minimum Function Test Statistic 0.000
Degrees of freedom 0
Minimum Function Value 0.0000000000000
Parameter Estimates:
Information Expected
Standard Errors Standard
Regressions:
Estimate Std.Err z-value P(>|z|)
Y ~
X (c) 0.036 0.104 0.348 0.728
M ~
X (a) 0.474 0.103 4.613 0.000
Y ~
M (b) 0.788 0.092 8.539 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.Y 0.898 0.127 7.071 0.000
.M 1.054 0.149 7.071 0.000
Defined Parameters:
Estimate Std.Err z-value P(>|z|)
ab 0.374 0.092 4.059 0.000
total 0.410 0.125 3.287 0.00114. 修正指標
可以通過在summary()函數中增加參數modindices = TRUE,來得出修正指標,例如:
fit <- cfa(HS.model,
data = HolzingerSwineford1939)
mi <- modindices(fit)
mi[mi$op == "=~",]結果為:
lhs op rhs mi epc sepc.lv sepc.all sepc.nox
25 visual =~ x4 1.211 0.077 0.069 0.059 0.059
26 visual =~ x5 7.441 -0.210 -0.189 -0.147 -0.147
27 visual =~ x6 2.843 0.111 0.100 0.092 0.092
28 visual =~ x7 18.631 -0.422 -0.380 -0.349 -0.349
29 visual =~ x8 4.295 -0.210 -0.189 -0.187 -0.187
30 visual =~ x9 36.411 0.577 0.519 0.515 0.515
31 textual =~ x1 8.903 0.350 0.347 0.297 0.297
32 textual =~ x2 0.017 -0.011 -0.011 -0.010 -0.010
33 textual =~ x3 9.151 -0.272 -0.269 -0.238 -0.238
34 textual =~ x7 0.098 -0.021 -0.021 -0.019 -0.019
35 textual =~ x8 3.359 -0.121 -0.120 -0.118 -0.118
36 textual =~ x9 4.796 0.138 0.137 0.136 0.136
37 speed =~ x1 0.014 0.024 0.015 0.013 0.013
38 speed =~ x2 1.580 -0.198 -0.123 -0.105 -0.105
39 speed =~ x3 0.716 0.136 0.084 0.075 0.075
40 speed =~ x4 0.003 -0.005 -0.003 -0.003 -0.003
41 speed =~ x5 0.201 -0.044 -0.027 -0.021 -0.021
42 speed =~ x6 0.273 0.044 0.027 0.025 0.025再根據MI(一般以4為標準)和EPC值進行調整。
15. 從擬合方程中提取信息
summary():結果概覽
parameterEstimates(fit):參數估計
fit <- cfa(HS.model, data=HolzingerSwineford1939)
parameterEstimates(fit)standardizedSolution():標準化參數估計
fit <- cfa(HS.model, data=HolzingerSwineford1939)
standardizedSolution(fit)fitted():擬合協方差矩陣和均值向量
fit <- cfa(HS.model, data=HolzingerSwineford1939)
fitted(fit)resid():擬合模型殘差,[觀測協方差矩陣/均值向量]和[隱含協方差矩陣/均值向量]的差
fit <- cfa(HS.model, data=HolzingerSwineford1939)
resid(fit, type="standardized")fitMeasures():返回所有擬合度量指標
fit <- cfa(HS.model, data=HolzingerSwineford1939)
fitMeasures(fit)
fitMeasures(fit, "cfi") # 提取某個具體指標,例如cfiinspect():查看擬合的lavaan對象具體信息



