Q: 棧、隊列與數組的區別? A: 本篇主要涉及三種數據存儲類型:棧、隊列和優先順序隊列,它與數組主要有如下三個區別: A: (一)程式員工具 數組和其他的結構(棧、隊列、鏈表、樹等等)都適用於資料庫應用中作為數據記錄。它們常用於記錄那些對應於現實世界的對象和活動的數據,如職員檔案等,這些結構便於數據 ...
Q: 棧、隊列與數組的區別?
A: 本篇主要涉及三種數據存儲類型:棧、隊列和優先順序隊列,它與數組主要有如下三個區別:
A: (一)程式員工具
數組和其他的結構(棧、隊列、鏈表、樹等等)都適用於資料庫應用中作為數據記錄。它們常用於記錄那些對應於現實世界的對象和活動的數據,如職員檔案等,這些結構便於數據的訪問:它們易於進行插入、刪除和查找特定數據項的操作。
然而,本篇要講解的數據結構和演算法更多的是作為程式員的工具來運用。它們主要作為構思演算法的輔助工具,而不是完全的數據存儲工具。這些數據結構的生命周期比那些資料庫類型的結構要短得多。在程式操作執行期間它們才被創建,通常用它們去執行某項特殊的任務;當完成任務之後,它們則被銷毀。
A: (二)受限訪問
在數組中,若知道數據項的下標,便可以立即訪問該數據項;而在本篇的數據結構中,訪問是受限制的,即在特定時刻只有一個數據項可以被讀取或者刪除。
這些結構介面的設計增強了這種受限訪問,訪問其他數據項理論上是不允許的。
A: (三)更加抽象
棧、隊列和優先隊列是比數組和其他數據存儲結構更為抽象的結構。主要是通過介面對棧、隊列和優先隊列進行定義,介面表明瞭它們可以完成的操作,而主要實現機制對用戶來說是不可見的。
例如:棧的實現機制可以用數組實現,本篇的示例就是這樣處理的,但它也可以用鏈表來實現。優先順序隊列的內部實現可以用數組或一種特別的樹-堆來實現。
Q: 什麼是棧?
A: 棧只允許訪問一個數據項:即最後插入的數據項。移除這個數據項才能訪問倒數第二個插入的數據項,以此類推。
Q: 棧有哪些實際場景?
A: 大部分微處理器運用基於棧的體繫結構,當調用一個方法時,把它的返回值和參數壓入棧,當方法結束返回時,哪些數據出棧。棧操作就嵌入在微處理器中。
Q: 棧的Java代碼?
A: 在本例中,StackX類裡面數據項的類型為long型,是用數組來實現,top變數存儲棧頂元素的下標。
示例: StackX.java, StackXTest.java
Q: 棧示例1:單詞逆序?
A: 棧的第一個例子是做一件非常簡單的事情:單詞逆序。因為棧的後進先出(LIFO)的特點,所以字母的順序就顛倒了。
Q: 棧示例2:分隔符匹配?
A: 棧通常用於匹配左分隔符和右分隔符,因為最後出現的左邊分隔符需要最先匹配,這個規律符合棧的LIFO的特點。
下麵是一些例子:
c[d] // correct
a{b[c]d}e // correct
a{b(c]d}e // not correct; ] doesn’t match (
a[b{c}d]e} // not correct; nothing matches final }
a{b(c) // not correct; nothing matches opening {
分隔符匹配程式從字元串中不斷地讀取字元,每次讀取一個字元。若發現它是左分隔符,將它壓入棧中。當讀到一個右分隔符時,彈出棧頂的左分隔符,並且查看它是否和右分隔符向匹配。(註:非分隔符的字元不插入棧中,只需忽略它們。)
Q: 棧的效率?
A: StackX類中實現的棧,入棧和出棧的時間複雜度為常數O(1), 棧操作所消耗的時間不依賴於棧中數據項的個數,因此操作時間很短。棧不需要比較和移動操作。
Q: 什麼是隊列?
A: 隊列(Queue)在詞典里是“排隊”(waiting line)的意思。電腦科學中,隊列是一種數據結構,有點類似棧,只是隊列中的第一個插入的數據項最先被移除(先進先出,FIFO),而在棧中,最後插入的數據項最先移除(LIFO)。
Q: 什麼是迴圈隊列?
A: 為了避免隊列不滿卻不能插入新數據項的問題,可以讓隊頭隊尾指針繞過到數組開始的位置,這就是迴圈隊列。
Q: 隊列有哪些實際的場景?
A: 使用文字處理器,敲擊一個鍵,而電腦又暫時要做其他的事情。敲擊的內容不會被丟失,它會在隊列中等待,知道文字處理程式有時間來讀取它。利用隊列保證了鍵入內容在處理時其順序不會改變。
Q: 隊列的Java代碼?
A: Queue類不但有mFront(隊頭)和mRear(隊尾),還有隊列當中當前數據項的個數mSize。
A: add/offer()方法
將指定的元素插入此隊列。區別在於add(e)會拋出異常,offer(e)返回特殊值。
內部調用insert()方法,一般情況,插入操作mRear(隊尾指針)加一後,在隊尾指針所指的位置處插入新的數據項。但是,當mRear指向數組的最後一個元素,即mItems.length - 1位置的時候,在插入數據項之前,它必須回到數組的第一個元素前面,即mRear設置為-1,因此當mRear加1後,它等於0,是數組第一個元素的下標值。最後,mSize加一。
A: remove()/poll()方法
獲取並移除此隊列的頭。區別在於remove(e)會拋出異常,poll(e)返回特殊值。
內部調用extract()方法,該方法總是由mFront指針得到隊頭數據項的值,然後將mFront加一。但是,如果這樣做mFront會超過數組的大小,mFront必須繞回到數組下標為0的位置上。註意先將返回值臨時存儲起來。最後mSize減一。
A: peek()方法
獲取但不移除此隊列的頭;如果此隊列為空,則返回NULL_ELEMENT。
A: 示例:Queue.java
Q: 沒有數據項計數欄位的隊列Java代碼?
A: 在Queue類中包含數據項計數欄位mSize會使insert()和extract()方法增加一點額外的操作,因為處理insert()和remove()方法必須分別遞增和遞減這個變數值。這可能算不上額外的開銷,但是如果處理大量的插入和移除操作,這就可能會影響性能。因此,一些隊列的實現不使用數據項計數的欄位,而是通過mFront和mRear來計算出隊列是否為空或者滿以及數據項的個數。
示例:Queue.java
Q: 隊列的效率?
A: 和棧一樣,隊列中插入數據項和移除數據項的時間複雜度均為O(1)
Q: 雙端隊列?
A: 略
Q: 優先順序隊列?
A: 優先順序隊列是不同於先進先出隊列的另一種隊列。每次從隊列中取出的是具有最高優先權的元素。
Q: 優先順序隊列有哪些實際場景?
A: 例如,在搶先式多任務操作系統中,程式排列在優先順序隊列中,這樣優先順序最高的程式會得到時間片並得以運行。
Q: 優先順序隊列的Java代碼?
A: 本示例使用有序數組實現優先順序隊列,這種方式插入比較慢,但是它比較簡單,適用於數據量比較小並且不是特別註重插入速度的情況。
A: 最小關鍵字值得數據項總是數組的高端(最高下標值處),而最大的數據項在低端(下標值為0的位置)。 
A: 待出隊的數據項總是在數組的高端,所以刪除操作又快又容易。刪除數據項後,隊頭指針下移指向隊列新的高端,不需要移動和比較。
A: 註意沒有指針迴繞,隊尾指針從不移動,它總是指著數組低端的元素。
A: Font和Rear指針是為了和普通隊列做比較,實際上並不需要它們。
A: 在數據項個數比較少,或不太關心速度的情況下,用數組實現優先順序隊列還可以滿足要求。如果數據項很多,或速度很重要時,採用堆是更好的選擇。
Q: 優先順序隊列的效率?
A: 本示例的優先順序隊列插入操作需要O(N)時間,而刪除操作則需要O(1)的時間。後面將介紹如何通過堆來改進插入操作的時間。
Q: 如何解析算術表達式?
A: 對於諸如 2*(3+4) 或者 ((2+4)*7)+3*(9-5)的算術表達式,前面我們已經演示了怎麼應用棧來檢查分隔符是否匹配正確,但是接下來我們將學習如何解析這些算術表達式。
事實上,對電腦演算法來說如果要直接求算術表達式的值還是相當困難,因此對於演算法來說分這兩步實現更容易:
1. 將算術表達式轉換成另一種形式:尾碼表達式
2. 計算尾碼表達式的值
Q: 中綴/尾碼表達式?
A: 中綴表達式:操作符放在兩個操作數之間。比如A+B或A/B等。
A: 尾碼表達式:也稱作逆波蘭表達式(Reverse Polish Notation或者RPN),它是由一位波蘭的數學家發明的。操作符跟在兩個操作數的後面,而且不包含括弧。這樣A+B 就變成AB+,A/B變成AB/。
A: 下麵是中綴表達式轉化為尾碼表達式的例子: 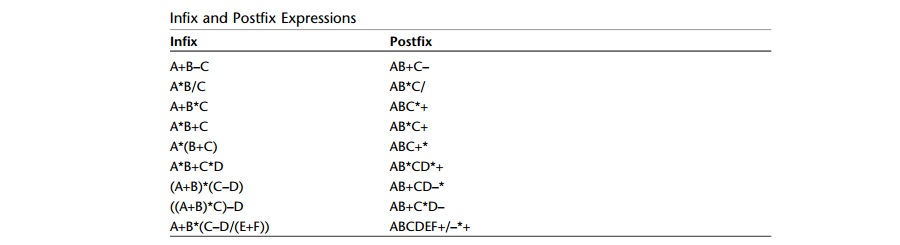
Q: 人類是如何計算中綴表達式?
A: 由於Mr. Klemmer的長期的教學教育,對於3+4+5或者3*(4+5)表達式,我們人類做起這個問題卻相當容易。通過分析人類如何計算這些表達式的值,可以得出轉化為尾碼表達式的啟示:
粗略地說,解析算術表達式時,應該遵循下列幾條規則:
1. 從左到右讀取算式
2. 已經讀到了可以計算值得兩個操作數和一個操作符時,就可以計算,並用計算結果代替那兩個操作數和哪個操作符
3.繼續這個過程--從左到右,能算就算--直到表達式的結尾。
A: 示例:3 + 4 - 5

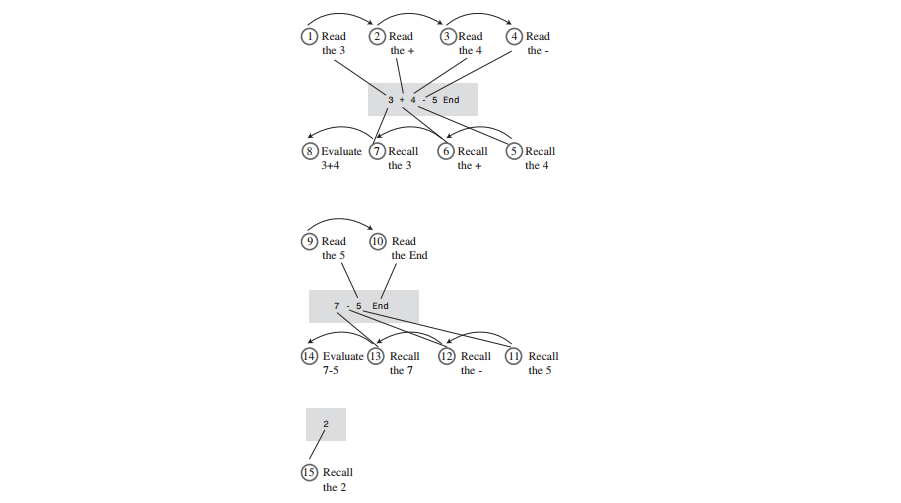
A: 示例: 3 + 4 * 5 

A: 示例: 3 * (4 + 5) 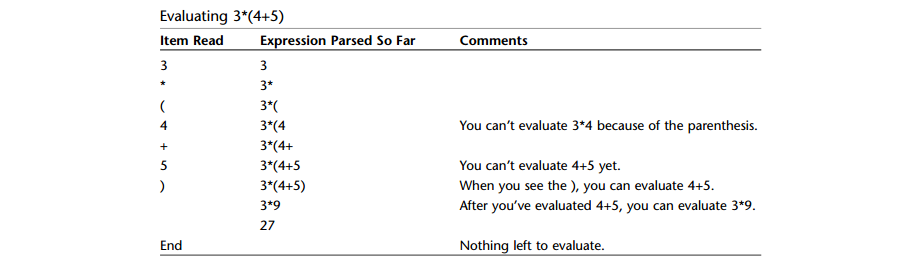
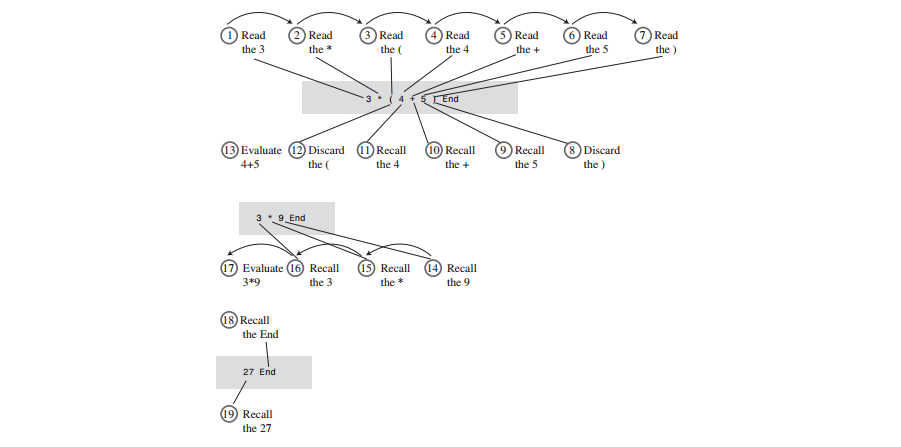
Q: 如何把中綴表達式轉換成尾碼表達式?
A: 正如前面看到的那樣,計算中綴表達式,既要向前,也要向後讀表達式。將中綴表達式轉換成尾碼表達式的規則和計算中綴表達式的規則類似。但是還是有點變化。
A: 將中綴表達式轉換成尾碼表達式不用做算術運算,它不求中綴表達式的值,只是把操作數和操作符重新排列成另一種形式。
A: 轉換規則: 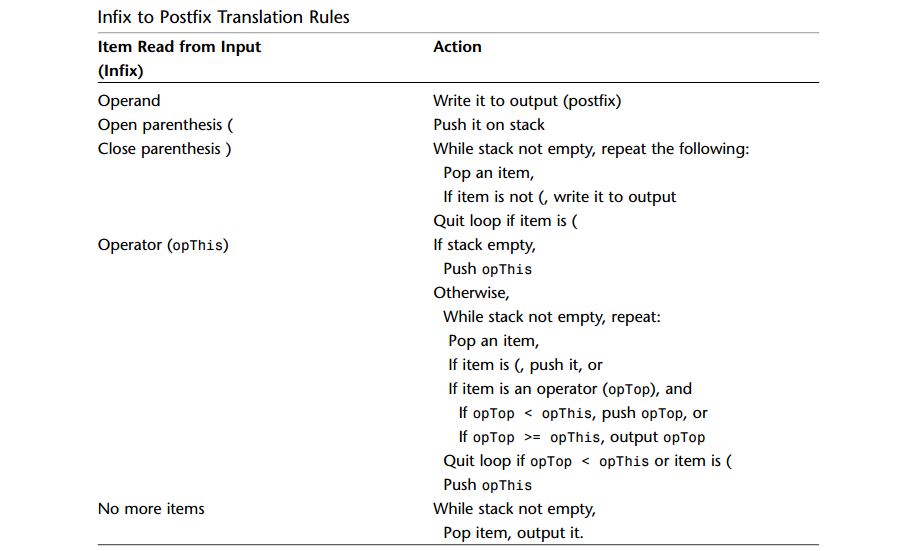
A: 示例:A+B-C 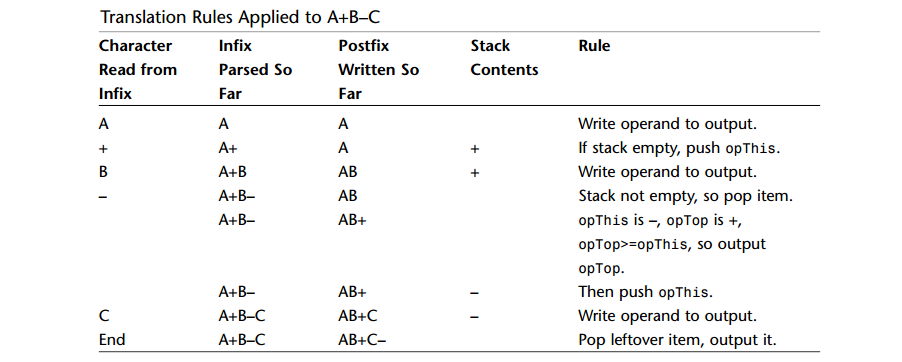
A: 示例:A+B*C 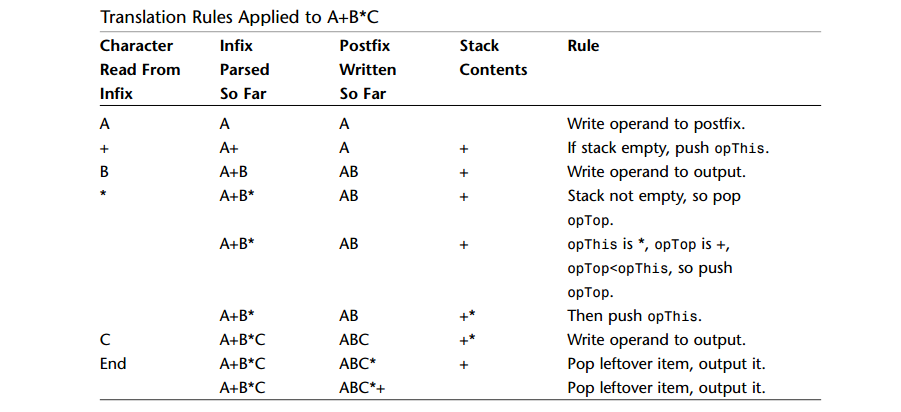
A: 示例:A*(B+C) 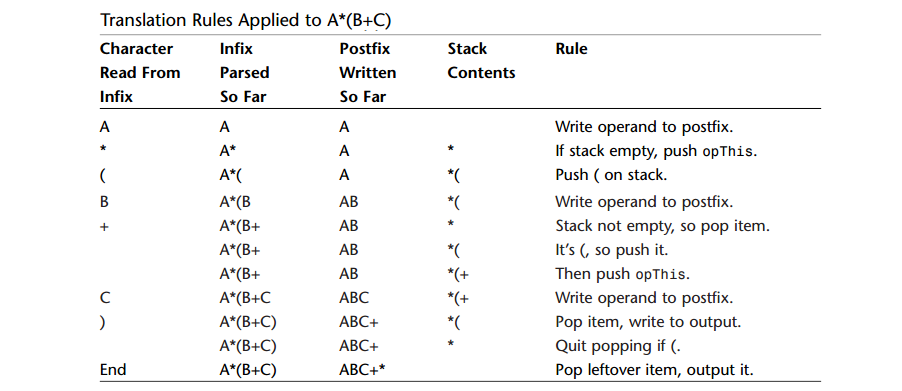
Q: 中綴表達式轉換成尾碼表達式的Java代碼 ?
A: 示例: In2PostTransform.java
Q: 人類如何用尾碼表達式求值?
A: 下圖展示了人類是如何通過觀察和鉛筆在紙上計算尾碼表達式的。
示例:345+*612+/– 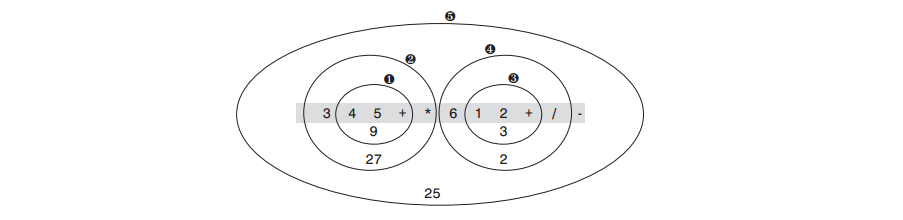
從左邊第一個操作符開始,把它和它左邊相鄰的兩個操作數畫在一個圓圈裡,然後應用操作符運算兩個操作數並把結果寫在圓圈裡。最大的圓圈裡算出來的值就是這個表達式最後的結果。
Q: 尾碼表達式求值的規則?
A: 怎麼才能寫一個程式來重覆剛纔的求值過程呢?正如上面所描述,每遇到一個操作符,就用它來運算在這之前最後看到的兩個操作數,這就表明可以利用棧來存儲操作數。它的規則如下: 
算術操作的結果被壓入到棧中,在最後一個字元(一定是操作符)被讀取並執行計算以後,棧里只剩一個數據項,它就是整個表達式的運算結果。
Q: 尾碼表達式求值的Java代碼?
A: 為了簡化代碼,這裡限制只能輸入一位數的數字。
示例:PostfixParser.java
Q: 本篇小結?
- 棧、隊列和優先順序隊列是經常用於簡化某些程式操作的數據結構。
- 在這些數據結構中,只有一個數據項可以被訪問。
- 棧只允許訪問最後一個插入的數據項。
- 隊列只允許訪問第一個插入的數據項。
- 隊列可以實現為迴圈隊列,它基於數組,數組下標可以從數組末端迴繞到數組的開始位置。
- 優先順序隊列的重要操作是有序地插入新數據項和移除關鍵字最小(有時是最大)的數據項。
- 這些數據結構可以用數組實現,也可以用其他機制(例如鏈表)來實現。
Q: 參考
- 《Java數據結構和演算法》Robert Lafore 著,第4章 - 棧和隊列



