HASH意為(散列),是OI的常用演算法。 我們常用哈希的原因是,hash可以快速(一般來說是O(段長))的求出一個子段的hash值,然後就可以快速的判斷兩個串是否相同。 今天先講string類的hash。 可以發現,與一個string有關的HASH值不僅僅跟每個字元的個數有關,還和字元的位子有關。 ...
HASH意為(散列),是OI的常用演算法。
我們常用哈希的原因是,hash可以快速(一般來說是O(段長))的求出一個子段的hash值,然後就可以快速的判斷兩個串是否相同。
今天先講string類的hash。
可以發現,與一個string有關的HASH值不僅僅跟每個字元的個數有關,還和字元的位子有關。
通過簡單的思考,我們可以構造如圖的模型:
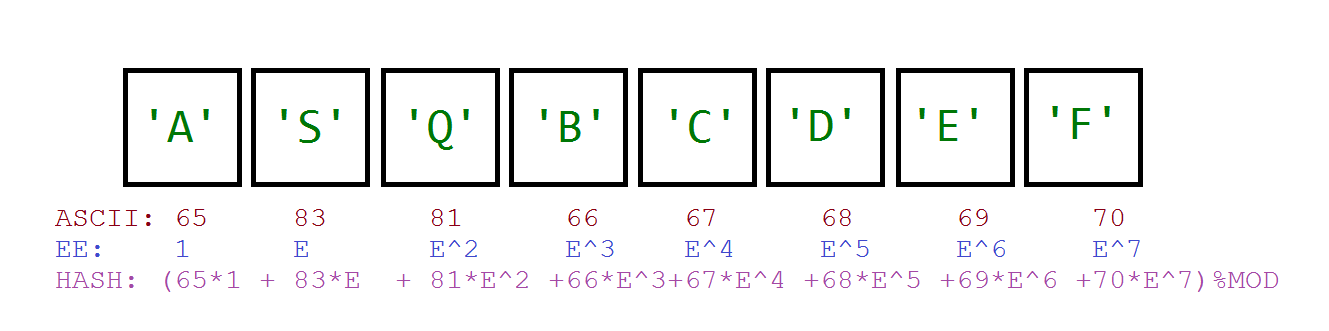
寫一個比較正常的hash模板吧
const int EE = 97;const int MOD = 100000007;
int HASH(string &p)
{
int E = 1;
int ret = 0;
int tl = p.size();
for (int i=0;i<tl;i++)
ret += E*p[i], E *= EE;
return ret;
}
題目來了:
KMP問題
題目描述
如題,給出兩個字元串s1和s2,其中s2為s1的子串,求出s2在s1中所有出現的位置。
輸入輸出格式
輸入格式:
第一行為一個字元串,即為s1
第二行為一個字元串,即為s2
輸出格式:
若幹行,每行包含一個整數,表示s2在s1中出現的位置
接下來1行,包括length(s2)個整數,表示首碼數組next[i]的值。
輸入輸出樣例
輸入樣例#1:ABABABC
ABA
輸出樣例#1:
1
3
說明
時空限制:1000ms,128M
數據規模:
設s1長度為N,s2長度為M
對於30%的數據:N<=15,M<=5
對於70%的數據:N<=10000,M<=100
對於100%的數據:N<=1000000,M<=1000000
思路
首先說明:此題正解為KMP,不為hash。如果想知道KMP演算法,請百度一下。
但是我們學的可是“hash”呀,不能直接預處理,如果直接預處理的話,時間為O(n*m),炸掉。
我們就可以遞推:
"已知長度為m的序列a[1]...a[m],現在已知"a[1]...a[m]"的hash值為K,欲求a[2]...a[m+1]的hash值。"
可以這一樣想:"改變EE的賦值方式,反過來賦值,這樣的話可以直接刪去第一個'a[1]*EE^(m-1)',再乘一個'EE',往後再移一位,再加上一個a[m+1]."
那麼,轉移方程也很容易寫了,為HASH[i]=(HASH[i-1]-a[i-2]*E[1]%M+M)%M*EE%M+a[i-2+m];(HASH[i]表示a[i-1]到a[i+m-2]的hash值。
另附代碼:
#include<cstdio>#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int n,k,len1,len2;
int next1[1000001];
char s1[1000001];
char s2[1000001];
long long HASH[1000001];
long long E[1000001],M=1234567898765;
long long EE = 97;
int init()
{
long long Key=0;
int ans=0;
memset(E,0,sizeof(E));
memset(HASH,0,sizeof(HASH));
E[len2]=1;
for (int i=len2-1;i>=1;i--)
E[i]=E[i+1]*EE%M;
for (int i=1;i<=len2;i++)
HASH[1]=(HASH[1]+E[i]*(s1[i-1]))%M;
for (int i=1;i<=len2;i++)
Key=(Key+E[i]*(s2[i-1]))%M;
if (HASH[1]==Key) ans++;
for (int i=2;i<=len1-len2+1;i++)
{
HASH[i]=(HASH[i-1]-s1[i-2]*E[1]%M+M)%M*EE%M+s1[i-2+len2];
if (HASH[i]==Key) ans++;
}
printf("%d\n",ans);
}
int main(){
scanf("%s",s1) ;
scanf("%s",s2) ;
len1=strlen(s1);
len2=strlen(s2);
init();
return 0;
}



