Coloring Brackets time limit per test: 2 seconds time limit per test: 2 seconds memory limit per test: 256 megabytes memory limit per test: 256 megaby ...
Coloring Brackets
time limit per test: 2 seconds memory limit per test: 256 megabytes input: standard input output: standard outputOnce Petya read a problem about a bracket sequence. He gave it much thought but didn't find a solution. Today you will face it.
You are given string s. It represents a correct bracket sequence. A correct bracket sequence is the sequence of opening ("(") and closing (")") brackets, such that it is possible to obtain a correct mathematical expression from it, inserting numbers and operators between the brackets. For example, such sequences as "(())()" and "()" are correct bracket sequences and such sequences as ")()" and "(()" are not.
In a correct bracket sequence each bracket corresponds to the matching bracket (an opening bracket corresponds to the matching closing bracket and vice versa). For example, in a bracket sequence shown of the figure below, the third bracket corresponds to the matching sixth one and the fifth bracket corresponds to the fourth one.
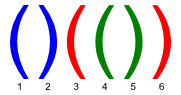
You are allowed to color some brackets in the bracket sequence so as all three conditions are fulfilled:
- Each bracket is either not colored any color, or is colored red, or is colored blue.
- For any pair of matching brackets exactly one of them is colored. In other words, for any bracket the following is true: either it or the matching bracket that corresponds to it is colored.
- No two neighboring colored brackets have the same color.
Find the number of different ways to color the bracket sequence. The ways should meet the above-given conditions. Two ways of coloring are considered different if they differ in the color of at least one bracket. As the result can be quite large, print it modulo 1000000007 (109 + 7).
Input
The first line contains the single string s (2 ≤ |s| ≤ 700) which represents a correct bracket sequence.
Output
Print the only number — the number of ways to color the bracket sequence that meet the above given conditions modulo 1000000007 (109 + 7).
Examples
Input
(())
Output
12
Input
(()())
Output
40
Input
()
Output
4
Note
Let's consider the first sample test. The bracket sequence from the sample can be colored, for example, as is shown on two figures below.


The two ways of coloring shown below are incorrect.


題目大意:給定一個合法的括弧序列,現在要你給括弧序列染色。但是必須要滿足如下條件:一、一個括弧可以不染色,或者染紅色,或者染藍色;二、一對匹配的括弧只能有一邊染色(這裡的匹配是唯一的對應,而不是只要是"()"就可,下同),且必須有一邊染色;三、相鄰的括弧染的顏色必須不一樣,但是可以都不染色。問你有多少種方案?因為方案數很大,所以結果模去1e9+7。
解題思路:容易看出這是一道DP題,並且是一道區間DP題。自己的DP很差,想了半天沒想出來。於是去網上搜了一下別人的解法,瞬間恍然大悟了。設dp[l][r][x][y]表示區間[l,r]左端染的色是x,右端染的色是y的方案數,其中x,y取0,1,2,分別表示不染色,染紅色,染藍色。則該區間有三種情況,如下:
1、l+1==r,那麼它們一定就是一對匹配的括弧,此時,只可能有四種情況,方案數均為1,即:dp[l][r][0][1] = dp[l][r][1][0] = 1;dp[l][r][0][2] = dp[l][r][2][0] = 1;
2、l和r是一對匹配的括弧,此時,區間被分為兩部分,兩端點以及區間[l+1,r-1],那麼我們可以先算出區間[l+1,r-1]的方案數,再由此狀態轉移到當前區間,兩端點情況也就四種,不衝突即可轉移,詳見代碼;
3、l和r不是一對匹配的括弧,此時,區間也可被分成兩部分,區間[l,mid]和區間[mid+1,r],其中mid為l所對應與之匹配的括弧,這樣,一個合法的括弧序列變成兩個合法的括弧序列,將它們分別求出方案數,再將不衝突的情況組合起來即可,詳見代碼。
附上AC代碼:

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int maxn = 705; 5 const int mod = 1000000007; 6 ll dp[maxn][maxn][3][3]; 7 string str; 8 stack<int> s; 9 map<int, int> pos; 10 11 void get_match(){ 12 for (int i=0; i<str.size(); ++i){ 13 if (str[i] == '(') 14 s.push(i); 15 else{ 16 pos[i] = s.top(); 17 pos[s.top()] = i; 18 s.pop(); 19 } 20 } 21 } 22 23 void dfs(int l, int r){ 24 if (l+1 == r){ 25 dp[l][r][0][1] = dp[l][r][1][0] = 1; 26 dp[l][r][0][2] = dp[l][r][2][0] = 1; 27 return ; 28 } 29 if (pos[l] == r){ 30 dfs(l+1, r-1); 31 for (int i=0; i<3; ++i) 32 for (int j=0; j<3; ++j){ 33 if (j != 1) 34 dp[l][r][0][1] = (dp[l][r][0][1]+dp[l+1][r-1][i][j])%mod; 35 if (j != 2) 36 dp[l][r][0][2] = (dp[l][r][0][2]+dp[l+1][r-1][i][j])%mod; 37 if (i != 1) 38 dp[l][r][1][0] = (dp[l][r][1][0]+dp[l+1][r-1][i][j])%mod; 39 if (i != 2) 40 dp[l][r][2][0] = (dp[l][r][2][0]+dp[l+1][r-1][i][j])%mod; 41 } 42 return ; 43 } 44 int mid = pos[l]; 45 dfs(l, mid); 46 dfs(mid+1, r); 47 for (int i=0; i<3; ++i) 48 for (int j=0; j<3; ++j) 49 for (int k=0; k<3; ++k) 50 for (int s=0; s<3; ++s) 51 if (!(k==1&&s==1) && !(k==2&&s==2)) 52 dp[l][r][i][j] = (dp[l][r][i][j]+dp[l][mid][i][k]*dp[mid+1][r][s][j])%mod; 53 } 54 55 int main(){ 56 ios::sync_with_stdio(false); 57 cin.tie(0); 58 cin >> str; 59 get_match(); 60 dfs(0, str.size()-1); 61 ll ans = 0; 62 for (int i=0; i<3; ++i) 63 for (int j=0; j<3; ++j) 64 ans = (ans+dp[0][str.size()-1][i][j])%mod; 65 cout << ans << endl; 66 return 0; 67 }View Code




