bzoj 1179[Apio2009]Atm (tarjan+spfa)

題目

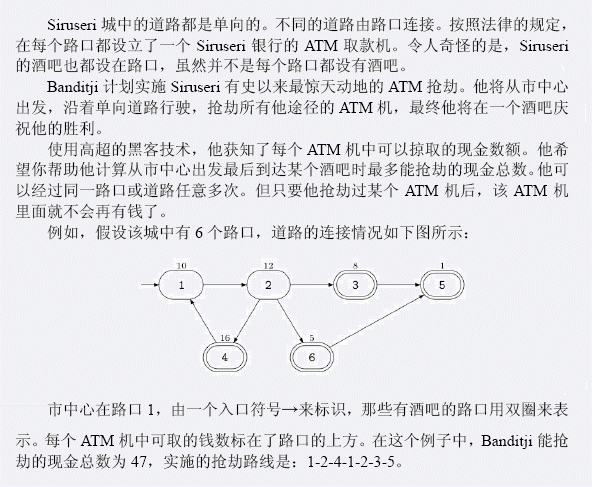
輸入

第一行包含兩個整數N、M。N表示路口的個數，M表示道路條數。接下來M行，每行兩個整數，這兩個整數都在1到N之間，第i+1行的兩個整數表示第i條道路的起點和終點的路口編號。接下來N行，每行一個整數，按順序表示每個路口處的ATM機中的錢數。接下來一行包含兩個整數S、P，S表示市中心的編號，也就是出發的路口。P表示酒吧數目。接下來的一行中有P個整數，表示P個有酒吧的路口的編號

輸出

輸出一個整數，表示Banditji從市中心開始到某個酒吧結束所能搶劫的最多的現金總數。

樣例輸入

6 7
1 2
2 3
3 5
2 4
4 1
2 6
6 5
10
12
8
16
1
5
1 4
4
3
5
6
樣例輸出

47
提示

50%的輸入保證N, M<=3000。所有的輸入保證N, M<=500000。每個ATM機中可取的錢數為一個非負整數且不超過4000。輸入數據保證你可以從市中心沿著Siruseri的單向的道路到達其中的至少一個酒吧。

 這道題我們需要用tarjan+spfa（用來跑最長路）

 首先要做的是把圖上的點跑一邊tarjan求出所有的強連通分量，把強連通分量上的點的父節點都設成該強連通分量的根

              //因為強連通分量上的點只要能到達一個就可以到達該強連通分量上的其它點，並且一條路可以走很多遍。

 再把所有強連通分量中的除了根以外的點上的值全部加到根上。

 然後將所有不在強連通分量中的點以及所有強連通分量的根為新的點，重新建圖

 對新建的圖進行spfa求最長路

 最後找出所有酒吧的父節點找出來，找出這些節點中到起點值最大的

              //因為強連通分量上的點只要能到達一個就可以到達該強連通分量上的其它點，並且一條路可以走很多遍。

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int cnt, hh[510000], hhh[510000], stack[510000];
int dfn[510000], low[510000], num, ans, q, top, w[510000];
int father[510000], dd[510000], j, n, h, t, l[510000], z, x, y, m, s, p;
bool d[510000];
struct node
{
    int v, next;
};
node b[510000], ss[510000];
void add(int aa, int bb)//連邊
{
    b[++cnt].v = bb;
    b[cnt].next = hh[aa];
    hh[aa] = cnt;
}
void addd(int aa, int bb)//連接新建圖上的邊
{
    ss[++cnt].v = bb;
    ss[cnt].next = hhh[aa];
    hhh[aa] = cnt;
}



void tarjan(int k)
{
    int i;
    dfn[k] = low[k] = ++num;
    stack[++top] = k;
    d[k] = true;
    for(i = hh[k]; i != 0; i = b[i].next)
    {
        int e = b[i].v;
        if(!dfn[e])
        {
            tarjan(e);
            low[k] = min(low[k], low[e]);
        }
        else if(d[e] == true)
        {
            low[k] = min(low[k], dfn[e]);
        }
    }
    if(dfn[k] == low[k])
    {
        d[k] = false;
        father[k] = k;
        while(stack[top] != k)
        {
            w[k] += w[stack[top]];
            father[stack[top]] = k;
            d[stack[top--]] = false;
        }
        top--;
    }

}
void rebuild()
{
    cnt = 0;
    int i;
    for(i = 1; i <= n; i++)
    {
        for(j = hh[i]; j != 0; j = b[j].next)
        {
            t = b[j].v;
            if(father[i] == father[t])continue;
            addd(father[i], father[t]);
        }
    }
}
void spfa()
{
    int i;
    q = s;
    memset(d, 0, sizeof(d));
    h = 0, t = 0;
    l[q] = w[q];
    d[q] = true;
    while(1)
    {
        if(h > t)break;

        for(i = hhh[q]; i != 0; i = ss[i].next)
        {
            z = ss[i].v;
            if(l[q] + w[z] > l[z])
            {
                l[z] = l[q] + w[z];
                if(d[z])continue;
                dd[++t] = z;
                d[z] = true;
            }
        }
        d[q] = false;
        q = dd[++h];
    }
}
int main()
{
    int i;
    scanf("%d %d", &n, &m);
    for(i = 1; i <= m; i++)
    {
        scanf("%d %d", &x, &y);
        add(x, y);
    }
    for(i = 1; i <= n; i++)
    {
        scanf("%d", &w[i]);
    }
    scanf("%d %d", &s, &p);
    for(j = 1; j <= n; j++)
    {
        if(!dfn[j])tarjan(j);
    }
    rebuild();//利用tarjan求出所有強連通分量

    s = father[s];//如果起點在一個強連通分量中，那麼將起點換成該強連通分量的根
                  //因為強連通分量上的點只要能到達一個就可以到達該強連通分量上的其它點，並且一條路可以走很多遍。
                  //重要的事說三遍

    spfa();//利用spfa求出最長路

    for(i = 1; i <= p; i++)
    {
        scanf("%d", &q);
        ans = max(ans, l[father[q]]);
    }
    printf("%d", ans);
    return 0;
}