一、前言 演算法（Algorithm）是指用來操作數據、解決程式問題的一組方法。對於同一個問題，使用不同的演算法，也許最終得到的結果是一樣的，但在過程中消耗的資源和時間卻會有很大的區別 衡量不同演算法之間的優劣主要是通過時間和空間兩個維度去考量： 時間維度：是指執行當前演算法所消耗的時間，我們通常用「時間復 ...
一、前言
演算法（Algorithm）是指用來操作數據、解決程式問題的一組方法。對於同一個問題，使用不同的演算法，也許最終得到的結果是一樣的，但在過程中消耗的資源和時間卻會有很大的區別
衡量不同演算法之間的優劣主要是通過時間和空間兩個維度去考量：
- 時間維度：是指執行當前演算法所消耗的時間，我們通常用「時間複雜度」來描述。
- 空間維度：是指執行當前演算法需要占用多少記憶體空間，我們通常用「空間複雜度」來描述
通常會遇到一種情況，時間和空間維度不能夠兼顧，需要在兩者之間取得一個平衡點是我們需要考慮的
一個演算法通常存在最好、平均、最壞三種情況，我們一般關註的是最壞情況
最壞情況是演算法運行時間的上界，對於某些演算法來說，最壞情況出現的比較頻繁，也意味著平均情況和最壞情況一樣差
二、時間複雜度
時間複雜度是指執行這個演算法所需要的計算工作量，其複雜度反映了程式執行時間「隨輸入規模增長而增長的量級」，在很大程度上能很好地反映出演算法的優劣與否
一個演算法花費的時間與演算法中語句的「執行次數成正比」，執行次數越多，花費的時間就越多
演算法的複雜度通常用大O符號表述，定義為T(n) = O(f(n))，常見的時間複雜度有：O(1)常數型、O(log n)對數型、O(n)線性型、O(nlogn)線性對數型、O(n^2)平方型、O(n^3)立方型、O(n^k)k次方型、O(2^n)指數型，如下圖所示：
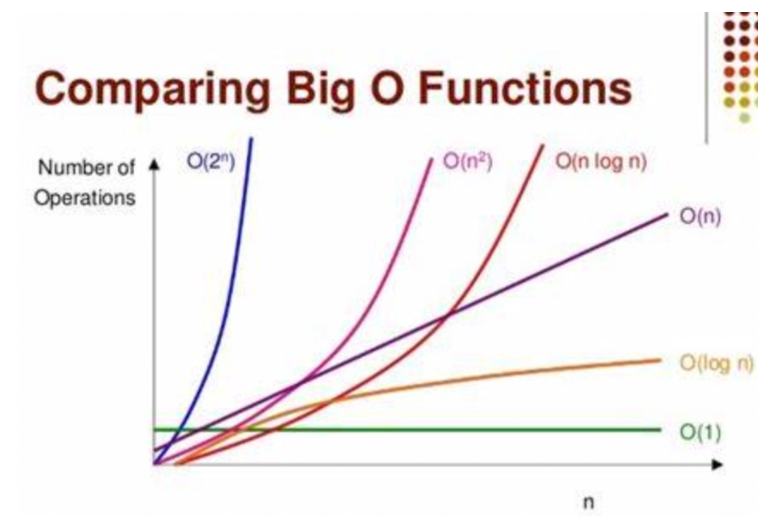
從上述可以看到，隨著問題規模n的不斷增大，上述時間複雜度不斷增大，演算法的執行效率越低，由小到大排序如下：
Ο(1)＜Ο(log n)＜Ο(n)＜Ο(nlog n)＜Ο(n2)＜Ο(n3)＜…＜Ο(2^n)＜Ο(n!)
註意的是，演算法複雜度只是描述演算法的增長趨勢，並不能說一個演算法一定比另外一個演算法高效，如果常數項過大的時候也會導致演算法的執行時間變長
關於如何計算時間複雜度，可以看看如下簡單例子：
function process(n) {
let a = 1
let b = 2
let sum = a + b
for(let i = 0; i < n; i++) {
sum += i
}
return sum
}
該函數演算法需要執行的運算次數用輸入大小n的函數表示，即 T(n) = 2 + n + 1，那麼時間複雜度為O(n + 3)，又因為時間複雜度只關註最高數量級，且與之繫數也沒有關係，因此上述的時間複雜度為O(n)
又比如下麵的例子：
function process(n) {
let count = 0
for(let i = 0; i < n; i++){
for(let i = 0; i < n; i++){
count += 1
}
}
}
迴圈裡面嵌套迴圈，外面的迴圈執行一次，裡面的迴圈執行n次，因此時間複雜度為 O(n*n*1 + 2) = O(n^2)
對於順序執行的語句，總的時間複雜度等於其中最大的時間複雜度，如下：
function process(n) {
let sum = 0
for(let i = 0; i < n; i++) {
sum += i
}
for(let i = 0; i < n; i++){
for(let i = 0; i < n; i++){
sum += 1
}
}
return sum
}
上述第一部分複雜度為O(n)，第二部分複雜度為O(n^2)，總複雜度為max(O(n^2), O(n)) = O(n^2)
又如下一個例子：
function process(n) {
let i = 1; // ①
while (i <= n) {
i = i * 2; // ②
}
}
迴圈語句中以2的倍數來逼近n，每次都乘以2。如果用公式表示就是1 * 2 * 2 * 2 … * 2 <=n，也就是說2的x次方小於等於n時會執行迴圈體，記作2^x <= n，於是得出x<=logn
因此迴圈在執行logn次之後，便結束，因此時間複雜度為O(logn)
同理，如果一個O(n)迴圈裡面嵌套O(logn)的迴圈，則時間複雜度為O(nlogn)，像O(n^3)無非也就是嵌套了三層O(n)迴圈
三、空間複雜度
空間複雜度主要指執行演算法所需記憶體的大小，用於對程式運行過程中所需要的臨時存儲空間的度量
除了需要存儲空間、指令、常數、變數和輸入數據外，還包括對數據進行操作的工作單元和存儲計算所需信息的輔助空間
下麵給出空間複雜度為O(1)的示例，如下
let a = 1 let b = 2 let c = 3
上述代碼的臨時空間不會隨著n的變化而變化，因此空間複雜度為O(1)
let arr []
for(i=1; i<=n; ++i){
arr.push(i)
}
上述可以看到，隨著n的增加，數組的占用的記憶體空間越大
通常來說，只要演算法不涉及到動態分配的空間，以及遞歸、棧所需的空間，空間複雜度通常為O(1)，一個一維數組a[n]，空間複雜度O(n)，二維數組為O(n^2)
參考文獻
-
https://juejin.cn/post/6844904167824162823#heading-7
-
https://zhuanlan.zhihu.com/p/50479555
-
https://cloud.tencent.com/developer/article/1769988
如果對您有所幫助，歡迎您點個關註，我會定時更新技術文檔，大家一起討論學習，一起進步。
