學了分塊,感覺這玩意好難啊,怎麼聽起來這麼簡單?【】【】分塊! 先推薦一個東西:loj 分塊全家桶! 首先,把一整個數組劈成 \(\sqrt n\) 塊是最優的!(當然如果你想寫一個 \(114514\) 塊的分塊也沒問題但他不優啊!) 長這樣: 這樣它的複雜度是: 預處理:\(O(n\sqrt n ...
學了分塊,感覺這玩意好難啊,怎麼聽起來這麼簡單?【】【】分塊!
先推薦一個東西:loj 分塊全家桶!
首先,把一整個數組劈成 \(\sqrt n\) 塊是最優的!(當然如果你想寫一個 \(114514\) 塊的分塊也沒問題但他不優啊!)
長這樣:
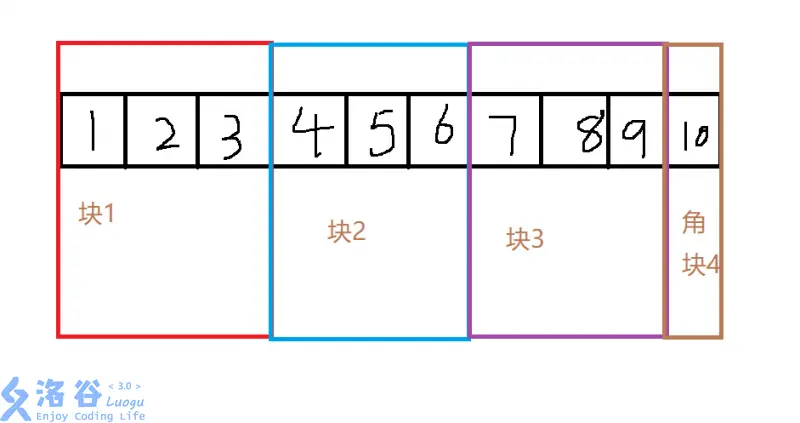
這樣它的複雜度是:
- 預處理:\(O(n\sqrt n+q)\)
- 線上處理:\(O(q\sqrt n+n)\)
分塊其實就是三層的樹,每個非葉子結點的節點有 \(\sqrt n\) 個子節點。
像這樣:
然後呢?
沒了。
你問咋處理?每個塊的處理,兩邊的“散塊”就暴力啊!
分塊的思路很簡單。
但某些毒瘤題的代碼不做評價。
T1
模板。只放代碼註釋不放解析。
本題代碼
#include<stdio.h>
#include<bits/stdc++.h>
#define N 1000010
#define MOD 998244353
#define esp 1e-8
#define INF 999999999999999999
#define LL long long
#define rep(i,a,b,g) for(LL i=a;i<=b;i+=g)
#define rem(i,a,b,g) for(LL i=a;i>=b;i-=g)
#define repn(i,a,b,g) for(LL i=a;i<b;i+=g)
#define remn(i,a,b,g) for(LL i=a;i>b;i-=g)
#define pll pair<LL,LL>
#define mkp(x,y) make_pair(x,y)
#define i128 __int128
#define lowbit(x) ((x)&(-(x)))
using namespace std;
void read(i128 &x)
{
i128 f=1;
x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
x*=f;
}
void write(i128 x)
{
if(x>=10)write(x/10);
putchar(x%10+'0');
}
LL n,a[50010],lz[50010],op,l,r,c,kc;
//kc:塊長(根號n),lz:類似lazytag,給整個塊的標記
LL q(LL x)
{
return lz[x/kc]+a[x];
}
void ud(LL l,LL r,LL c)
{
if(l/kc==r/kc)
{
rep(i,l,r,1)
{
a[i]+=c;
}
}
else
{
rep(i,l,(l/kc+1)*kc-1,1)a[i]+=c;
rep(i,r/kc*kc,r,1)a[i]+=c;
//兩邊的散塊
repn(i,l/kc+1,r/kc,1)lz[i]+=c;
//中間的整塊
}
}
int main()
{
cin>>n;
kc=sqrt(n);
rep(i,1,n,1)cin>>a[i];
rep(i,1,n,1)
{
cin>>op>>l>>r>>c;
if(!op)
{
ud(l,r,c);
}
else
{
cout<<q(r)<<endl;
}
}
return 0;
}



