卡爾曼濾波器(Kalman filter)是一種高效的遞歸濾波器, 能夠從一系列包含噪音的測量值中估計動態系統的狀態. 因為不需要存儲歷史狀態, 沒有複雜計算, 非常適合在資源有限的嵌入式系統中使用. 常用於飛行器的導引, 導航及控制, 機械和金融中的時間序列分析, 軌跡最佳化等. 本文對卡爾曼濾波... ...

卡爾曼濾波器(Kalman filter)是一種高效的遞歸濾波器, 能夠從一系列包含噪音的測量值中估計動態系統的狀態. 因為不需要存儲歷史狀態, 沒有複雜計算, 非常適合在資源有限的嵌入式系統中使用. 常用於飛行器的導引, 導航及控制, 機械和金融中的時間序列分析, 軌跡最佳化等. 卡爾曼濾波不需要假設誤差是正態分佈, 但如果誤差屬於正態分佈, 卡爾曼濾波的結果會更為準確.

卡爾曼濾波的計算分二個步驟: 預測與更新. 在預測階段, 濾波器基於上一步的預測結果, 預測當前狀態和誤差; 在更新階段, 濾波器利用當前的測量值和預測值, 計算得到新的狀態值和誤差.

Original Error Estimate, calculate the Kalman Gain using Error in Estimate and Error in Data(Measurement)
預測階段, 用預測誤差和測量誤差計算卡爾曼增益
Original Estimate, calculate Current Estimate using Kalman Gain, Previous Estimate and Measured Value
更新階段, 結合測量值, 用卡爾曼增益計算當前的狀態
Calculate the new Error in Estimate
計算新的預測誤差

定義

完整的卡爾曼濾波定義是這樣的

Predict step 預測階段
- State prediction 預測系統狀態:
  $\hat{x_{t|t-1}} = F_t \hat{x_{t-1|t-1}} + B_t u_t$
- Uncertainty prediction 預測誤差:
  $P_{t|t-1} = F_t P_{t-1|t-1} F_t^T + Q_t$
Update step 更新階段
- Kalman gain 更新卡爾曼增益:
  $K_t = \frac{P_{t|t-1} H_t^T} {H_t P_{t|t-1} H_t^T + R_t}$
- State update 更新狀態:
  $\hat{x_{t|t}} = \hat{x_{t|t-1}} + K_t (z_t - H_t \hat{x_{t|t-1}})$
- Uncertainty update 更新誤差:
  $P_{t|t} = (I - K_t H_t) P_{t|t-1}$

對以上符號的說明

$\hat{x}$: 預測的系統狀態向量
The state vector, which represents the true state of the system that we want to estimate.
$t$: 時間序列
The time step index, corresponding to different time periods.
$F_t$: 狀態轉移矩陣
The state transition matrix, which models how the system evolves from time step $t-1$ to $t$ without taking into account external factors.
$B_t$: 控制輸入矩陣
The control input matrix, used to incorporate the effect of any external factors $u_t$ (e.g., motors or steer engines inputs).
$u_t$: 控制輸入向量
The control input vector, containing the external factors impacting the system.
$P$: 誤差矩陣
The uncertainty (covariance) matrix, which quantifies our uncertainty about the estimated state.
$Q_t$: 過程雜訊協方差矩陣
The process noise covariance matrix, representing the estimation error caused by our simplified model of the system state dynamics. Q矩陣表示系統模型的過程雜訊, 系統模型是一個近似值, 在系統狀態的整個生命周期中, 系統模型的準確性會發生波動, Q矩陣用於表示這種不確定性, 並增加了狀態上的現有雜訊. 例如飛行器電機的震動給加速度的讀數帶來的誤差.
$H_t$: 觀察值轉換矩陣
The observation matrix, which models how the true system state is transformed into the observed system state.
$K_t$: 卡爾曼增益
The Kalman gain, which determines how much we trust the new observation relative to our prediction. 卡爾曼增益是一個介於0到1之間的數, 用於表示在預測中觀察值所占的比重, 卡爾曼增益越大說明雜訊越大, 觀察值越重要.
$z_t$: 觀察值(測量值)向量
The observation (measurement) vector, containing the recorded states.
$R_t$: 測量雜訊協方差矩陣
測量雜訊指的是測量工具(如感測器)測量時的固有雜訊, 例如在靜止時加速度感測器讀數的上下波動, The observation noise covariance matrix, representing the measurement noise in the observed states.
$I$: 單位矩陣
The identity matrix.

簡化

對於一個靜止(或勻速運動)的物體觀測加速度和角速度, 可以忽略控制輸入 $B_t$ 和 $u_t$, 將 $F_t$, $H_t$視為單位矩陣, 卡爾曼計算公式可以簡化為

Predict step 預測階段,
- State prediction 預測狀態等於前一步的狀態:
  $\hat{x_{t|t-1}} = \hat{x_{t-1|t-1}}$
- Uncertainty prediction 預測誤差等於更新後的誤差加上過程雜訊:
  $P_{t|t-1} = P_{t-1|t-1} + Q_t$
Update step 更新階段,
- Kalman gain 更新卡爾曼增益:
  $K_t = \frac{P_{t|t-1}} {P_{t|t-1} + R_t}$
- State update 更新狀態:
  $\hat{x_{t|t}} = \hat{x_{t|t-1}} + K_t (z_t - \hat{x_{t|t-1}})$
- Uncertainty update 更新誤差:
  $P_{t|t} = (I - K_t) P_{t|t-1}$

實例

1. 初始化

令預測誤差初始值為 $P = 10000$
測量誤差$σ = 0.1$，方差 $σ^2 = 0.01$, 即 $R$ 為固定的 0.01
雜訊方差為 $q = 0.15$
令初始預測值 $ \hat{x} = 10 $
預測誤差 $ P = P + q = 10000 + 0.15 = 10000.15 $

2. 觀察值 $Z = 50.486$

卡爾曼增益

$K = \frac{P}{P + r} = \frac{10000.15}{10000.15 + 0.01} = 0.99999$

更新系統狀態(等於預測狀態)

$\hat{x} = \hat{x} + K * (Z - \hat{x}) = 10 + 0.99999 * (50.486 - 10) = 50.486$

更新預測誤差

$P = (1 - K) * P = (1 - 0.99999) * 10000.15 = 0.01$

$P = P + q = 0.01 + 0.15 = 0.16$

3. 觀察值 $Z = 50.963$

卡爾曼增益

$K = \frac{P}{P + r} = \frac{0.16}{0.16 + 0.01} = 0.9412$

更新系統狀態(等於預測狀態)

$\hat{x} = \hat{x} + K * (Z - \hat{x}) = 50.486 + 0.9412 * (50.963 - 50.486) = 50.934$

更新預測誤差

$P = (1 - K) * P = (1 - 0.9412) * 0.16 = 0.0094$

$P = P + q = 0.0094 + 0.15 = 0.1594$

可以看到 $P$ 和 $K$ 的值迅速收斂

實現

一個簡單的C語言演示代碼, 會輸出每次迭代後產生的K增益, P誤差和預測值.

#include <stdio.h>

const int measures[] = {
  -269,   -255,   -130,    228,   -437,  -1234,   1247,    173,   -400,  -1561,  -1038,    207,    958,   -516,   -581,   -716,    -18,  -1193,   -989,   -593,    484,    102,    718,   1362,   1563,   2683,    428,   1616,   2922,   2968,   3046,   3572,   4006,   4821,   3964,   3127,   3086,   3190,   3682,   4015,   4471,   4211,   4523,   5098,   6452,   5947,   6150,   5694,   6498,   7048,   7519,   6820,   5652,   6608,   7409,   8729,  10569,  10760,   9054,   9856,   8656,   7972,   9320,   6958,   6820,   7391,   7702,   8248,   9426,   8812,   8666,   8838,   7943,   6878,   7233,   7536,   8381,   8314,   7267,   6704,   7343,   6321,   6409,   6023,   7334,   7975,   7659,   6159,   5990,   6187,   6645,   6702,   6273,   7196,   7381,   6939,   4201,   4108,   5338,   6469,   4528,   3679,   4113,   4158,   3428,   2966,   3466,   3704,   3220,   2582,   2818,   3039,   2835,   1929,   1362,    890,    396,   -201,   -992,  -1502,  -2009,  -1667,  -1503,  -1881,  -2713,  -3231,  -2856,  -2868,  -2989,  -4140,  -4878,  -4690,  -3838,  -4244,  -5312,  -9966,  -6514,  -5246,  -4559,  -4832,  -6833,  -8869,  -9207,  -8021,  -7959,  -9219, -10911, -12606, -12296, -11710, -10460, -10827, -13095, -12183, -10989,  -9458,  -9520, -10622, -12221, -11792,  -9510,  -7964,  -7935,  -8728,  -9137,  -8076,  -6628,  -6379,  -7132,  -8076,  -7499,  -6536,  -5855,  -6285,  -7310,  -7517,  -7217,  -6997,  -6440,  -5806,  -4647,  -4006,  -4144,  -3800,  -2820,  -1811,    215,    768,    531,    186,    514,   2117,   2618,   2396,   1600,   1477,   1800,   2329,   2015,   1585,   1461
};

static float k_gain, r_noise, q_noise, x_est, p_err, z_measure;


void Kalman_Init(void)
{
  p_err = 1.0;
  r_noise = 10.0;
  q_noise = 1;
  x_est = -200.0;

  p_err = p_err + q_noise;
}

float Kalman_Update(float measure)
{
  k_gain = p_err / (p_err + r_noise);
  x_est = x_est + k_gain * (measure - x_est);
  p_err = (1 - k_gain) * p_err;
  p_err = p_err + q_noise;
  return x_est;
}

int main(int argc, char *const argv[])
{
  int i;
  float estimate, new_measure;

  Kalman_Init();

  for (i = 0; i < sizeof(measures)/sizeof(int); i++)
  {
    estimate = Kalman_Update((float)measures[i]);
    printf("%3d: %6d %10.5f %10.5f %10.5f\r\n", i, measures[i], k_gain, p_err, estimate);
  }
  return 0;
}

對參數的說明

measures數值來自於手持物體旋轉時陀螺儀感測器的真實讀數, 本例中陀螺儀的實測雜訊$R$在10至20這個數量級, 運動中的抖動來源於手持產生的抖動
p_err = 1.0; 和 x_est = -200.0;, 預測和誤差的初始值可以隨意取一個接近的值, 如果不知道取什麼值, 設為0也問題不大.
r_noise = 10.0; 和 q_noise = 1; 這兩個值會顯著影響結果, 其中r_noise可以使用感測器收集靜止狀態數據後計算方差得到, q_noise無法明確計算, 初始可以賦0.1至1之間的數.

輸出結果格式

  0:   -269    0.04762    0.97619  -12.80952
  1:   -255    0.08894    1.38937  -34.34924
  2:   -130    0.12199    1.71988  -46.01752
  3:    228    0.14675    1.96749   -5.80566
  4:   -437    0.16440    2.14403  -76.69533
  5:  -1234    0.17655    2.26550 -281.01764
  6:   1247    0.18471    2.34705    1.21512
  7:    173    0.19009    2.40090   33.86971
  8:   -400    0.19361    2.43607  -50.13048
  9:  -1561    0.19589    2.45887 -346.09082
 10:  -1038    0.19736    2.47359 -482.64551
 11:    207    0.19831    2.48306 -345.88443
 12:    958    0.19891    2.48915  -86.52280
 13:   -516    0.19930    2.49305 -172.11964
 14:   -581    0.19955    2.49555 -253.71368
 15:   -716    0.19971    2.49715 -346.03918
 16:    -18    0.19982    2.49818 -280.49121
 17:  -1193    0.19988    2.49883 -462.88641
...

使用不同的 r_noise 和 q_noise 得到的變化曲線如圖

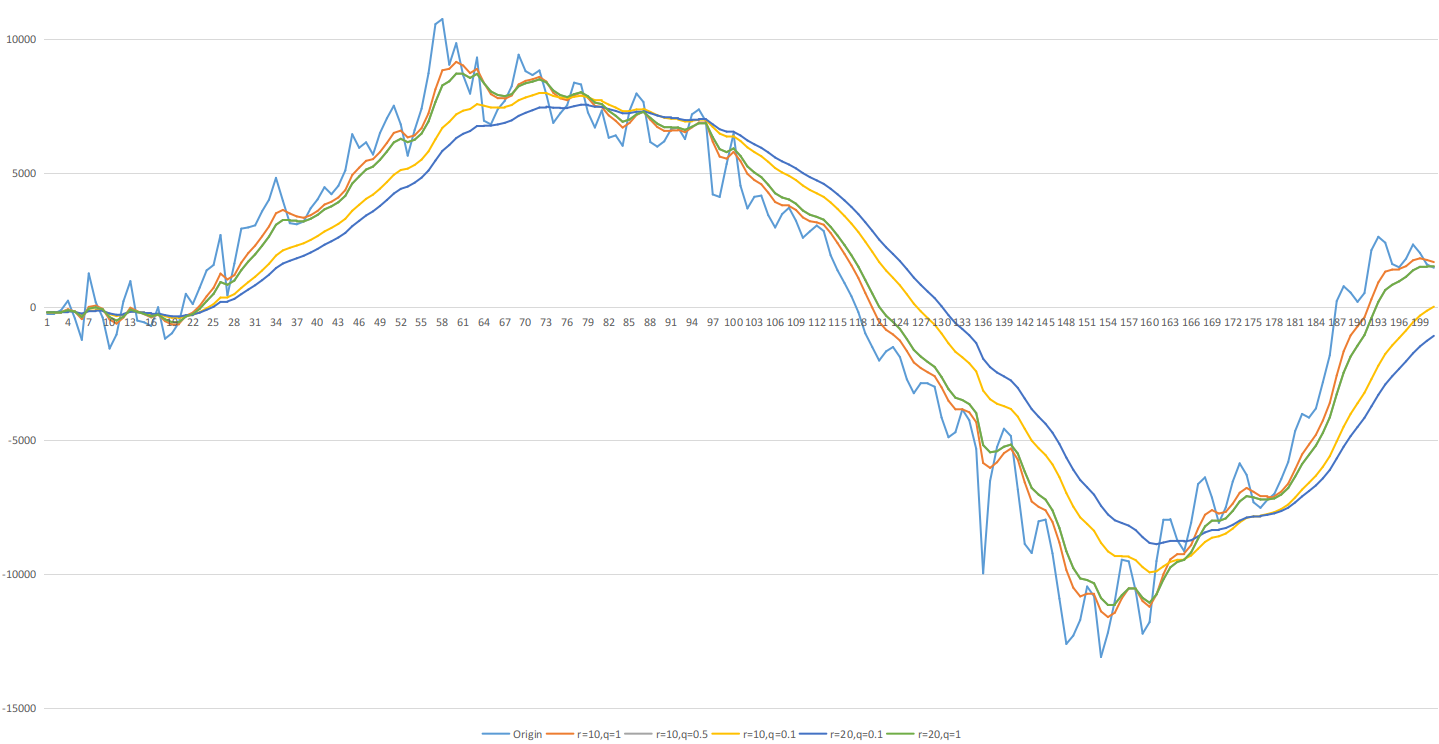
圖中變化最劇烈的藍色曲線是從感測器得到的原始測量值, 可以看到原始數據的抖動是很明顯的, 經過卡爾曼濾波後可以明顯消除抖變, 使結果數據更平滑.

通過變換多種雜訊組合, 可以觀察到的現象有

在r_noise 和 q_noise 不變的情況下, 不管 p_err 和 x_est 設置什麼初始值, 都會很快收斂, 最後輸出相同的結果序列(這點沒有在本例體現, 需要自己驗證)
r_noise越大表示測量雜訊越大, 測量值的權重越低, r_noise越大, 結果越平滑但是延遲也越大
q_noise是系統的固有誤差, q_noise越小, 結果越平滑延遲越大
r_noise 和 q_noise 等比例變化時, 產生的結果序列不變, 圖中 r=10,q=0.5 和 r=20,q=1 這兩個曲線是重合的.

總結

從卡爾曼濾波器的定義看

整個過程中, 對狀態 $\hat{x}$ 的預測和更新, 除了自身和觀測值$z_t$之外, 關係到這幾個參數 $F_t, B_t, u_t, K_t, H_t$, 其中 $F_t, u_t, H_t$ 在系統中都相對固定, 而 $B_t$ 是已知輸入, 例如電機或舵機的動作, 已知且確定的, 不存在雜訊, 真正起作用的是 $K_t$ 這個參數.
而 $K_t$ 這個參數的計算, 和 $\hat{x}$ 沒關係. 系統中不存在反饋, 觀測值 $z_t$ 和預測值 $\hat{x}$ 都不會影響 $K_t$, 只要 $H_t, R_t, Q_t$ 這三個值固定, 最後 $K_t$ 會收斂為一個常量

當符合上面兩點條件時, 狀態的更新公式就變成下麵的式子

$\hat{x_{t|t}} = \hat{x_{t|t-1}} + K_t (z_t - \hat{x_{t|t-1}}) \\ = \hat{x_{t|t-1}} + K_t z_t - K_t \hat{x_{t|t-1}} \\ = (1 - K_t) \hat{x_{t|t-1}} + K_t z_t$

令 $\beta = 1 - K_t$, 這就是一個典型的離散序列差分方程(difference equation)構成的低通濾波器

$\hat{x_{t|t}} = \beta \hat{x_{t|t-1}} + (1 - \beta) z_t$

在實際使用中, $Q$和$R$大概率是常數, 增益$K_t$會快速收斂, 上面的式子更簡單, 更容易理解和實現, 也符合它的典型使用方式, 即手動調整$\beta$ (等價於調整$Q$和$R$), 在延遲和平滑之間找到最佳平衡.