本文向大家介紹了最小二乘法以及公式推導的過程,並使用C#與Python進行實現。重點介紹了C#中是如何實現的,同時介紹了在C#中如何使用OxyPlot繪圖。希望對你有所幫助。 ...
最小二乘法介紹✨
最小二乘法(Least Squares Method)是一種常見的數學優化技術,廣泛應用於數據擬合、回歸分析和參數估計等領域。其目標是通過最小化殘差平方和來找到一組參數,使得模型預測值與觀測值之間的差異最小化。
最小二乘法的原理✨
線性回歸模型將因變數 (y) 與至少一個自變數 (x) 之間的關係建立為:
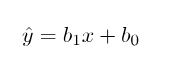
在 OLS 方法中,我們必須選擇一個b1和b0的值,以便將 y 的實際值和擬合值之間的差值的平方和最小化。
平方和的公式如下:
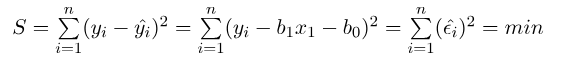
我們可以把它看成是一個關於b1和b0的函數,分別對b1和b0求偏導,然後讓偏導等於0,就可以得到最小平方和對應的b1和b0的值。
先說結果,斜率最後推導出來如下所示:
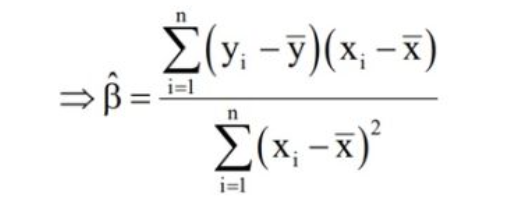
截距推導出來結果如下:
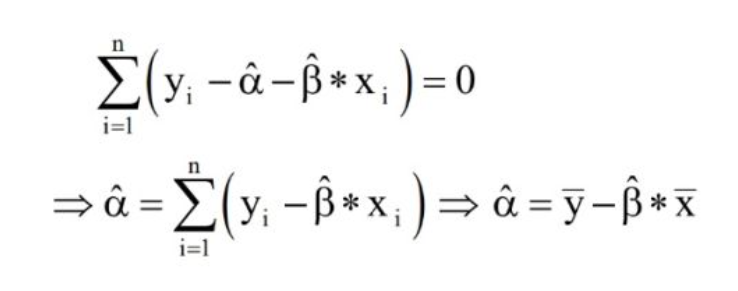
don't worry about that,慢慢推導總是可以弄明白的(不感興趣可以直接略過):

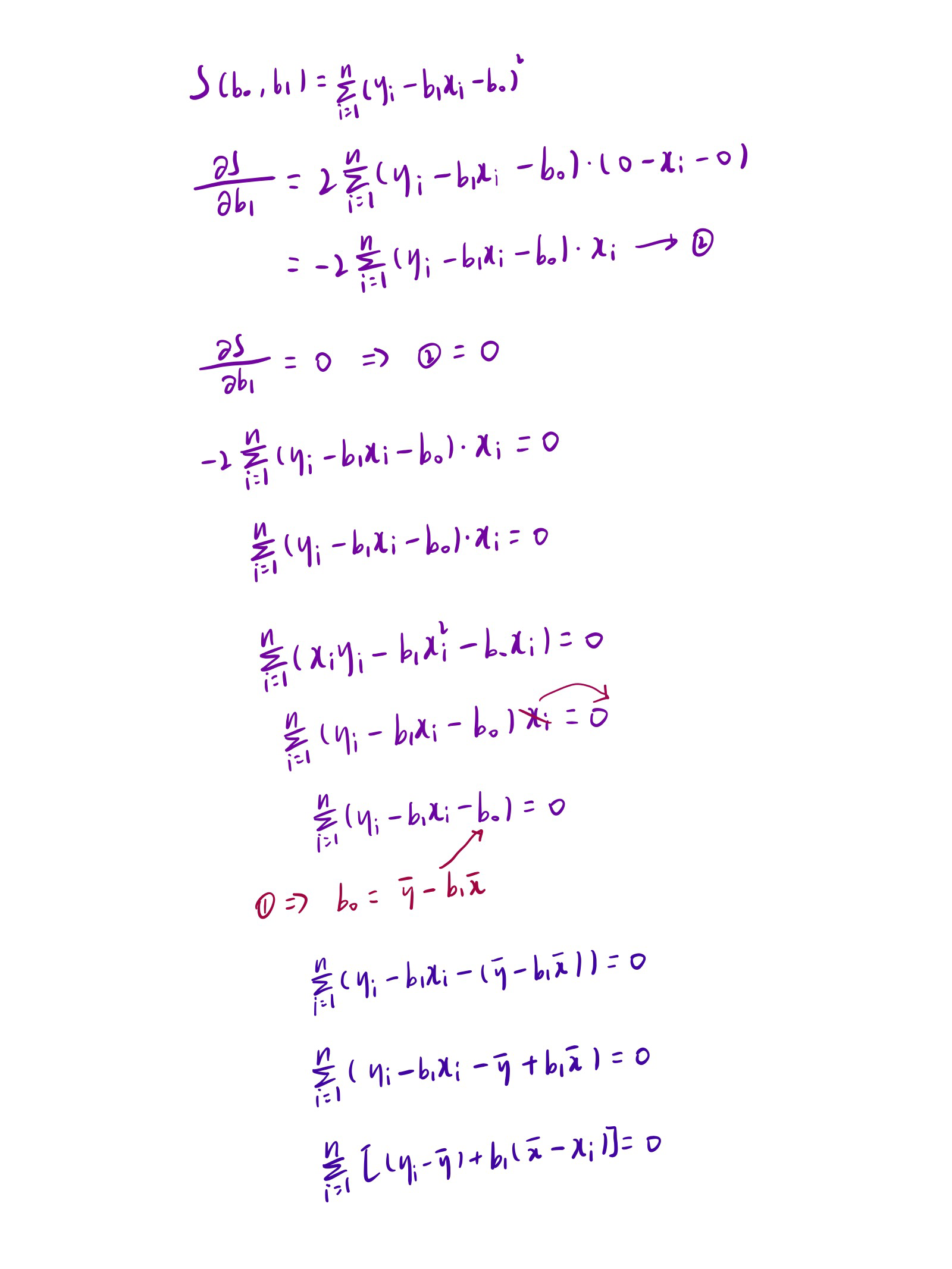
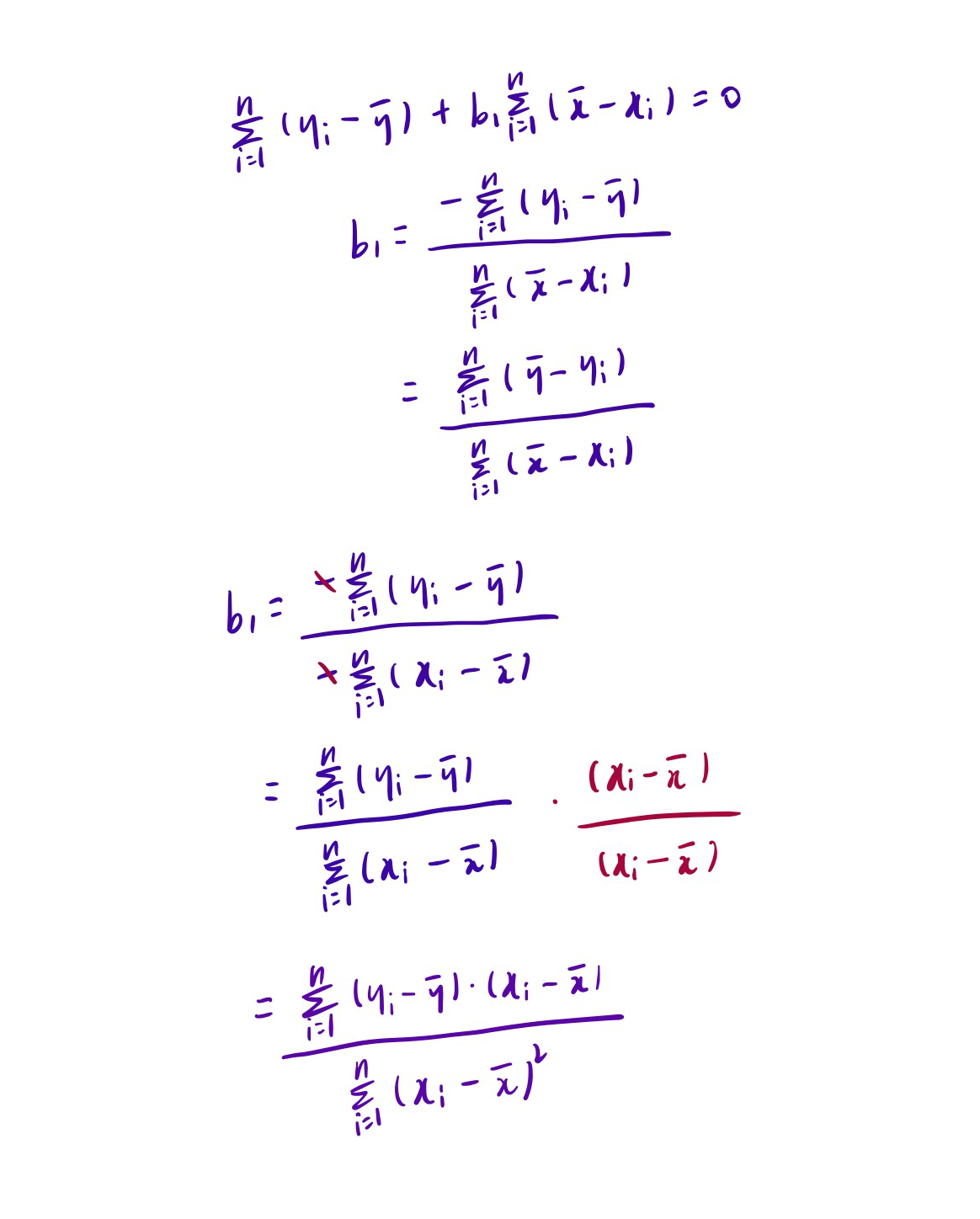
用C#實現最小二乘法✨
創建數據點✨
首先創建想要擬合的數據點:
NDArray? x, y;
x,y為全局變數。
//使用NumSharp創建線性回歸的數據集
x = np.arange(0, 10, 0.2);
y = 2 * x + 3 + np.random.normal(0, 3, x.size);
使用到了NumSharp,需要為項目添加NumSharp包:

x = np.arange(0, 10, 0.2);
的意思是x從0增加到10(不包含10),步長為0.2:

np.random.normal(0, 3, x.size);
的意思是生成了一個均值為0,標準差為3,數量與x數組長度相同的正態分佈隨機數數組。這個數組被用作線性回歸數據的雜訊。
使用OxyPlot畫散點圖✨
OxyPlot是一個用於在.NET應用程式中創建數據可視化圖表的開源圖表庫。它提供了豐富的功能和靈活性,使開發者能夠輕鬆地在其應用程式中集成各種類型的圖表,包括折線圖、柱狀圖、餅圖等。
添加OxyPlot.WindowsForms包:

將PlotView控制項添加到窗體設計器上:
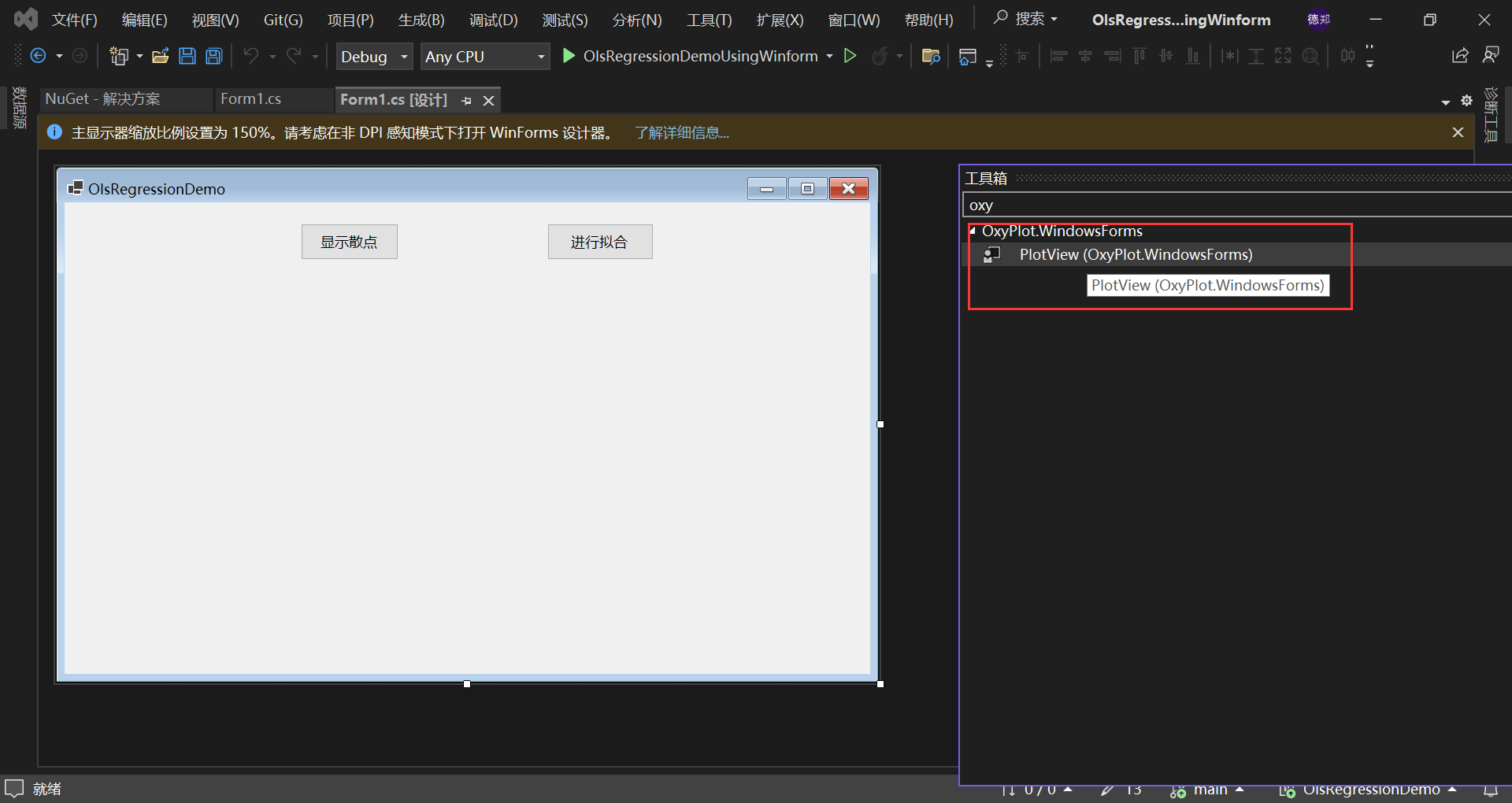
// 初始化散點圖數據
var scatterSeries = new ScatterSeries
{
MarkerType = MarkerType.Circle,
MarkerSize = 5,
MarkerFill = OxyColors.Blue
};
表示標誌為圓形,標誌用藍色填充,標誌的大小為5。
for (int i = 0; i < x.size; i++)
{
scatterSeries.Points.Add(new ScatterPoint(x[i], y[i]));
}
添加數據點。
PlotModel? plotModel;
將plotModel設置為全局變數。
// 創建 PlotModel
plotModel = new PlotModel()
{
Title = "散點圖"
};
plotModel.Series.Add(scatterSeries);
// 將 PlotModel 設置到 PlotView
plotView1.Model = plotModel;
這樣就成功繪製了散點圖,效果如下所示:
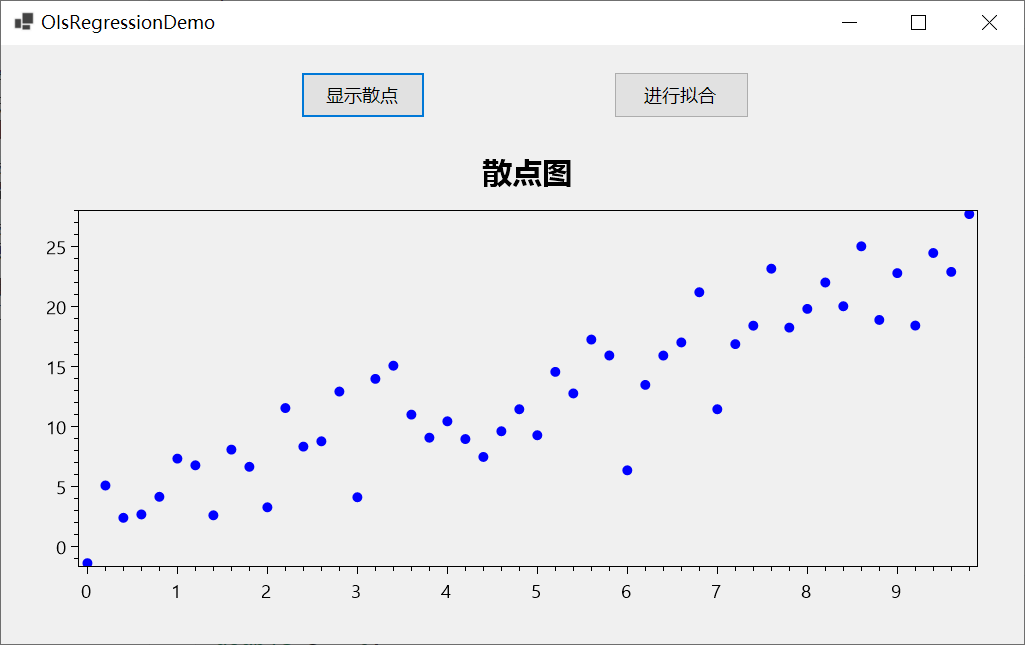
使用最小二乘法擬合數據點✨
double a = 0;
double c = 0;
double x_mean = x?.mean();
double y_mean = y?.mean();
//計算a和c
for(int i = 0; i < x?.size; i++)
{
a += (x[i] - x_mean) * (y?[i] - y_mean);
c += (x[i] - x_mean) * (x[i] - x_mean);
}
//計算斜率和截距
double m = a / c;
double b = y_mean - m * x_mean;
//擬合的直線
var y2 = m * x + b;
套用公式就可以,a表示上面斜率公式的上面那部分,c表示上面斜率公式的下麵那部分。
double x_mean = x?.mean();
double y_mean = y?.mean();
計算x與y的平均值。
使用OxyPlot畫擬合出來的直線✨
//畫這條直線
var lineSeries = new LineSeries
{
Points = { new DataPoint(x?[0], y2[0]), new DataPoint(x?[-1], y2[-1]) },
Color = OxyColors.Red
};
// 創建 PlotModel
plotModel?.Series.Add(lineSeries);
// 為圖表添加標題
if (plotModel != null)
{
plotModel.Title = $"擬合的直線 y = {m:0.00}x + {b:0.00}";
}
// 刷新 PlotView
plotView1.InvalidatePlot(true);
Points = { new DataPoint(x?[0], y2[0]), new DataPoint(x?[-1], y2[-1]) },
畫直線只要添加兩個點就好了x?[0], y2[0]表示x和y的第一個點,x?[-1], y2[-1])表示x和y的最後一個點,使用了NumSharp的切片語法。
畫出來的效果如下所示:
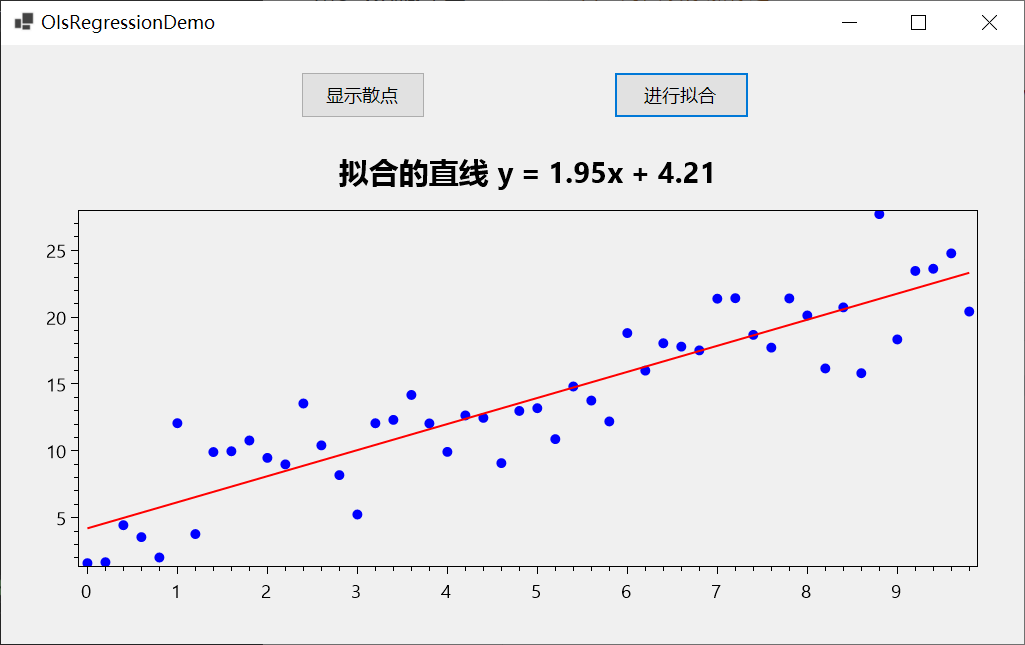
C#實現的全部代碼:
using NumSharp;
using OxyPlot.Series;
using OxyPlot;
namespace OlsRegressionDemoUsingWinform
{
public partial class Form1 : Form
{
NDArray? x, y;
PlotModel? plotModel;
public Form1()
{
InitializeComponent();
}
private void button1_Click(object sender, EventArgs e)
{
//使用NumSharp創建線性回歸的數據集
x = np.arange(0, 10, 0.2);
y = 2 * x + 3 + np.random.normal(0, 3, x.size);
// 初始化散點圖數據
var scatterSeries = new ScatterSeries
{
MarkerType = MarkerType.Circle,
MarkerSize = 5,
MarkerFill = OxyColors.Blue
};
for (int i = 0; i < x.size; i++)
{
scatterSeries.Points.Add(new ScatterPoint(x[i], y[i]));
}
// 創建 PlotModel
plotModel = new PlotModel()
{
Title = "散點圖"
};
plotModel.Series.Add(scatterSeries);
// 將 PlotModel 設置到 PlotView
plotView1.Model = plotModel;
}
private void button2_Click(object sender, EventArgs e)
{
double a = 0;
double c = 0;
double x_mean = x?.mean();
double y_mean = y?.mean();
//計算a和c
for(int i = 0; i < x?.size; i++)
{
a += (x[i] - x_mean) * (y?[i] - y_mean);
c += (x[i] - x_mean) * (x[i] - x_mean);
}
