AVL樹 AVL樹是一種自平衡二叉搜索樹。在這種樹中,任何節點的兩個子樹的高度差被嚴格控制在1以內。這確保了樹的平衡,從而保證了搜索、插入和刪除操作的高效性。AVL樹是由Georgy Adelson-Velsky和Evgenii Landis在1962年發明的,因此得名(Adelson-Velsky ...
AVL樹
AVL樹是一種自平衡二叉搜索樹。在這種樹中,任何節點的兩個子樹的高度差被嚴格控制在1以內。這確保了樹的平衡,從而保證了搜索、插入和刪除操作的高效性。AVL樹是由Georgy Adelson-Velsky和Evgenii Landis在1962年發明的,因此得名(Adelson-Velsky和Landis樹)。
平衡因數:每個節點的平衡因數是其左子樹的高度減去其右子樹的高度。平衡因數必須保持在-1、0或1之間。
旋轉操作:為了維持平衡,在進行插入或刪除操作後,可能會執行單旋轉或雙旋轉。單旋轉包括右旋(針對左重失衡)和左旋(針對右重失衡)。雙旋轉是一種更複雜的調整,包括左-右旋轉和右-左旋轉。
時間複雜度:在AVL樹中,查找、插入和刪除操作的時間複雜度均為O(log n),其中n是樹中的節點數。
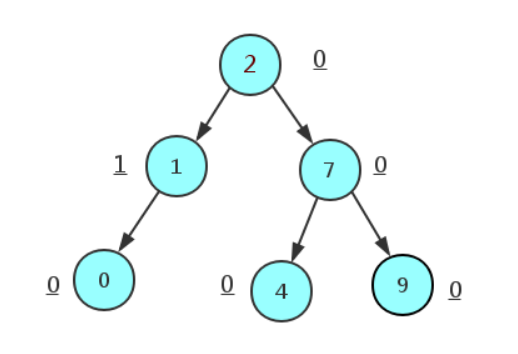
AVL樹節點定義
class AVLNode: def __init__(self, key): self.key = key self.height = 1 self.left = None self.right = None
這裡定義了一個AVL樹的節點。每個節點有一個鍵值key,一個高度屬性height,以及指向左右子節點的指針left和right。
AVL樹的高度和平衡因數
AVL樹的關鍵是保持每個節點的平衡。平衡因數被定義為節點的左子樹高度減去其右子樹高度。這個因數應該是-1、0或1。如果在任何時候,一個節點的平衡因數不在這個範圍內,我們需要通過旋轉來重新平衡樹。
def get_height(node): if not node: return 0 return node.height def get_balance(node): if not node: return 0 return get_height(node.left) - get_height(node.right)
這兩個函數幫助我們計算任何節點的高度和平衡因數。
AVL樹旋轉操作
為了維持平衡,我們可能需要進行樹的旋轉操作。主要有四種類型的旋轉:右旋轉、左旋轉、左-右旋轉和右-左旋轉。
-
右旋轉:
當一個節點的左子樹比右子樹高時,我們進行右旋轉。 def rotate_right(z): y = z.left T3 = y.right y.right = z z.left = T3 z.height = 1 + max(get_height(z.left), get_height(z.right)) y.height = 1 + max(get_height(y.left), get_height(y.right)) return y
-
左旋轉:
當一個節點的右子樹比左子樹高時,我們進行左旋轉。
def rotate_left(z): y = z.right T2 = y.left y.left = z z.right = T2 z.height = 1 + max(get_height(z.left), get_height(z.right)) y.height = 1 + max(get_height(y.left), get_height(y.right)) return y
-
左-右旋轉和右-左旋轉:
這些是雙旋轉操作,先進行一次旋轉使其成為第一種或第二種情況,然後再進行相應的旋轉。
AVL樹插入操作
插入操作類似於普通的二叉搜索樹插入,但是在插入後,我們需要更新祖先節點的高度,並檢查每個節點的平衡因數,以確保樹保持平衡。
def insert(node, key): if not node: return AVLNode(key) elif key < node.key: node.left = insert(node.left, key) else: node.right = insert(node.right, key) node.height = 1 + max(get_height(node.left), get_height(node.right)) balance = get_balance(node) if balance > 1 and key < node.left.key: return rotate_right(node) if balance < -1 and key > node.right.key: return rotate_left(node) if balance > 1 and key > node.left.key: node.left = rotate_left(node.left) return rotate_right(node) if balance < -1 and key < node.right.key: node.right = rotate_right(node.right) return rotate_left(node) return node
AVL樹刪除操作
刪除操作也與普通的二叉搜索樹類似,但在刪除節點後,我們需要更新祖先節點的高度,並檢查每個節點的平衡因數以重新平衡樹。
def min_value_node(node): current = node while current.left is not None: current = current.left return current def delete(node, key): if not node: return node if key < node.key: node.left = delete(node.left, key) elif key > node.key: node.right = delete(node.right, key) else: if node.left is None: temp = node.right node = None return temp elif node.right is None: temp = node.left node = None return temp temp = min_value_node(node.right) node.key = temp.key node.right = delete(node.right, temp.key) if node is None: return node node.height = 1 + max(get_height(node.left), get_height(node.right)) balance = get_balance(node) if balance > 1 and get_balance(node.left) >= 0: return rotate_right(node) if balance < -1 and get_balance(node.right) <= 0: return rotate_left(node) if balance > 1 and get_balance(node.left) < 0: node.left = rotate_left(node.left) return rotate_right(node) if balance < -1 and get_balance(node.right) > 0: node.right = rotate_right(node.right) return rotate_left(node) return node
這個刪除函數處理了三種情況:要刪除的節點有兩個子節點、一個子節點或沒有子節點。在刪除節點後,它會通過旋轉操作確保樹保持平衡。
使用AVL樹
現在我們可以創建一個AVL樹的實例,併進行插入和刪除操作:
avl_tree = None keys = [20, 4, 15, 70, 50, 80, 100] for key in keys: avl_tree = insert(avl_tree, key) avl_tree = delete(avl_tree, 70)
在這個例子中,我們插入了一些數字,然後刪除了一個。
紅黑樹
紅黑樹是另一種自平衡二叉搜索樹,它通過確保樹從根到葉子的最長可能路徑不超過最短可能路徑的兩倍來維持大致的平衡。
紅黑樹的節點有兩種顏色:紅色或黑色。這種樹遵循以下重要屬性:
顏色屬性:每個節點要麼是紅色,要麼是黑色。
根屬性:樹的根總是黑色。
葉子屬性:所有葉子(NIL節點)都是黑色。
紅色節點屬性:如果一個節點是紅色的,那麼它的兩個子節點都是黑色的。
路徑屬性:從任一節點到其每個葉子的所有路徑都包含相同數量的黑色節點。
紅黑樹通過旋轉和重新著色來維持這些屬性。雖然紅黑樹的平衡性不如AVL樹,但它在插入和刪除操作中需要更少的旋轉,這使得它在某些類型的應用中更高效。

紅黑樹節點定義:
class RedBlackNode: def __init__(self, key, color="red"): self.key = key self.color = color self.left = None self.right = None self.parent = None
這裡定義了一個紅黑樹的節點。除了常規的key外,節點還包含一個color屬性以及指向父節點和子節點的鏈接。
紅黑樹旋轉操作:
為了維持紅黑樹的特性,在插入和刪除節點時可能需要進行樹的旋轉操作。主要有兩種類型的旋轉:左旋和右旋。
-
左旋:
當一個節點的右子節點是紅色而左子節點是黑色時進行。
def rotate_left(self, x): y = x.right x.right = y.left if y.left != self.TNULL: y.left.parent = x y.parent = x.parent if x.parent == None: self.root = y elif x == x.parent.left: x.parent.left = y else: x.parent.right = y y.left = x x.parent = y
-
右旋:
當一個節點的左子節點是紅色而左子節點的左子節點也是紅色時進行。
def rotate_right(self, x): y = x.left x.left = y.right if y.right != self.TNULL: y.right.parent = x y.parent = x.parent if x.parent == None: self.root = y elif x == x.parent.right: x.parent.right = y else: x.parent.left = y y.right = x x.parent = y
紅黑樹插入操作:
插入操作首先類似於普通的二叉搜索樹插入。但在插入一個節點後,可能需要進行多次顏色更改和旋轉來修複可能違反的紅黑樹性質。
def insert(self, key): node = RedBlackNode(key) node.parent = None node.key = key node.left = self.TNULL node.right = self.TNULL node.color = 1 # 新節點必須是紅色 y = None x = self.root while x != self.TNULL: y = x if node.key < x.key: x = x.left else: x = x.right node.parent = y if y == None: self.root = node elif node.key < y.key: y.left = node else: y.right = node if node.parent == None: node.color = 0 return if node.parent.parent == None: return self.fix_insert(node)
在插入節點後,fix_insert函數被調用以重新平衡樹,確保樹仍然是一個有效的紅黑樹。
紅黑樹刪除操作:
刪除操作比插入操作更複雜。刪除節點後,可能需要進行多次顏色更改和旋轉來修複可能違反的紅黑樹性質。
def delete_node(self, node, key): # 省略具體刪除邏輯 self.fix_delete(x)
在刪除節點後,fix_delete函數被調用以重新平衡樹。
使用紅黑樹:
現在我們可以創建一個紅黑樹的實例,併進行插入和刪除操作:
rbt = RedBlackTree() numbers = [20, 15, 25, 10, 30, 5, 35] for number in numbers: rbt.insert(number) rbt.delete_node(rbt.root, 15)
在這個例子中,我們插入了一些數字,然後刪除了一個。
紅黑樹是一種複雜的數據結構,它通過一系列精心設計的規則和操作來確保樹的平衡。儘管它的實現比普通的二叉搜索樹複雜得多,但它在插入、刪除和查找操作上提供了良好的最壞情況性能。這種平衡是通過確保任何路徑上的黑色節點數目大致相同來實現的。紅黑樹廣泛應用於電腦科學的許多領域,尤其是在那些需要快速查找操作的場景中,如資料庫和文件系統。
實現紅黑樹要求對它的性質和操作有深入的理解。上述代碼提供了一個基本的框架,但它並不完整。在實際應用中,您可能還需要處理更多的邊界情況和優化。每個操作背後都有複雜的邏輯和數學原理,這是理解和實現紅黑樹的關鍵部分。
From:BigQuant量化平臺 —— 《AVL樹和紅黑樹的Python代碼實現》



