二叉樹（binary tree）

来源:https://www.cnblogs.com/dupengpeng/archive/2023/09/12/17695088.html
-Advertisement-
Play Games

二叉樹（binary tree） 二叉樹（Binary Tree）是一種常見的樹狀數據結構，它由一組節點組成，每個節點最多有兩個子節點，分別稱為左子節點和右子節點。二叉樹具有以下特點： 每個節點最多有兩個子節點，分別稱為左子節點和右子節點。 左子樹和右子樹也是二叉樹，它們的結構與父節點類似。 二叉樹 ...


二叉樹（binary tree）

二叉樹（Binary Tree）是一種常見的樹狀數據結構，它由一組節點組成，每個節點最多有兩個子節點，分別稱為左子節點和右子節點。二叉樹具有以下特點：

  1. 每個節點最多有兩個子節點，分別稱為左子節點和右子節點。
  2. 左子樹和右子樹也是二叉樹，它們的結構與父節點類似。
  3. 二叉樹的順序不固定，可以是任意形狀。

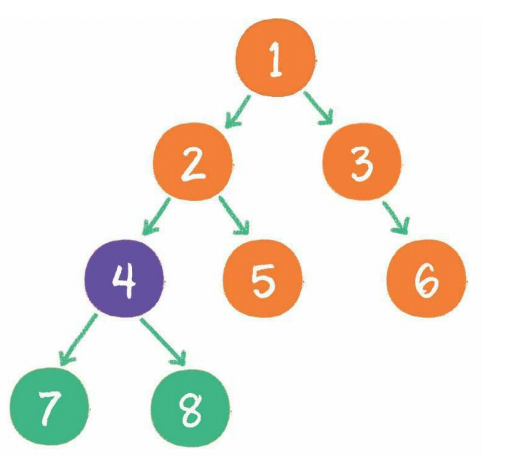
兩種特殊形式

二叉樹還有兩種特殊形式，一個叫作滿二叉樹 ，另一個叫作完全二叉樹

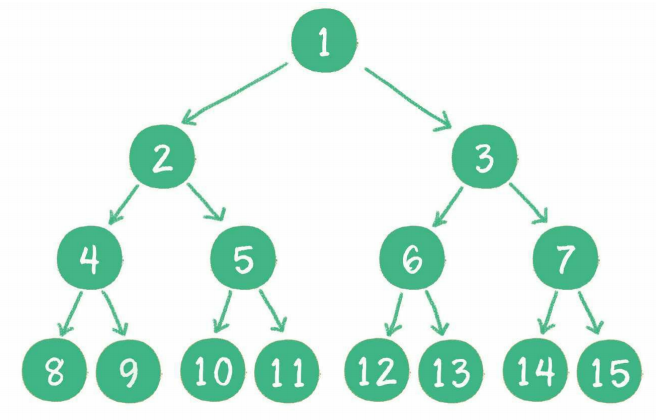
滿二叉樹

如果該二叉樹的所有葉子節點都在最後一層，並且結點總數= 2^n -1,n 為層數，則我們稱為滿二又樹。簡單點說，滿二叉樹的每一個分支都是滿的。

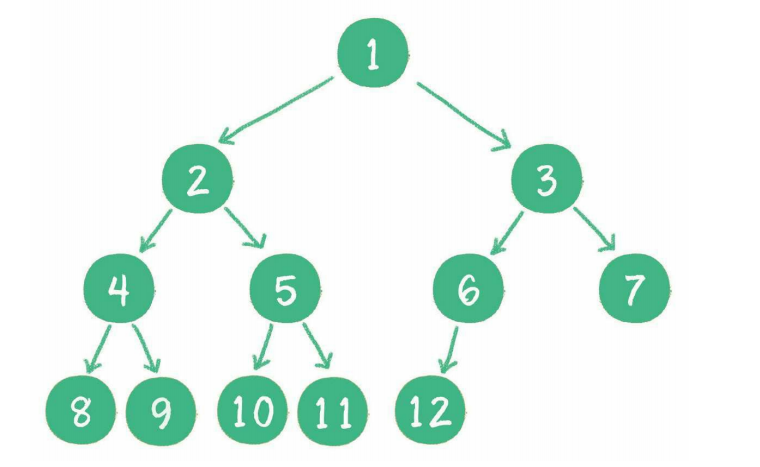
完全二叉樹

對一個有n個節點的二叉樹，按層級順序編號，則所有節點的編號為從1到n。如果這個樹所有節點和同樣深度的滿二叉樹的編號為從1到n的節點位置相同，則這個二叉樹為完全二叉樹。完全二叉樹的條件沒有滿二叉樹那麼苛刻: 滿二叉樹要求所有分支都是滿的;而完全二叉樹只需保證最後一個節點之前的節點都齊全即可。

遍歷二叉樹

在電腦程式中，遍歷本身是一個線性操作。所以遍歷同樣具有線性結構的數組或鏈表，是一件輕而易舉的事情。反觀二叉樹，是典型的非線性數據結構，遍歷時需要把非線性關聯的點轉化成一個線性的序列，以不同的方式來遍歷，遍歷出的序列順序也不同。

遍歷方式

深度優先和廣度優先這兩個概念不止局限於二叉樹，它們更是一種抽象的演算法思想，決定了訪問某些複雜數據結構的順序。在訪問樹、圖，或其他一些複雜數據結構時，這兩個概念常常被使用到。

1.深度優先遍歷（Depth-First Search，DFS）

所謂深度優先，顧名思義，就是偏向於縱深，“一頭扎到底”的訪問方式。可能這種說法有些抽象，下麵就通過二叉樹的前序遍歷、中序遍歷、後序遍歷 ，來看一看深度優先

2.廣度優先遍歷 (Breadth-First Search，BFS)

如果說深度優先遍歷是在一個方向上“一頭扎到底”，那麼廣度優先遍歷則恰恰相反:先在各個方向上各走出1步，再在各個方向上走出第2步、第3步......一直到各個方向全部走完。聽起來有些抽象，下麵讓我們通過二叉樹的層序遍歷

也是一種遍歷或搜索樹或圖的演算法。在廣度優先遍歷中，從根節點開始，按照層級順序逐層訪問節點，先訪問當前層的所有節點，然後再訪問下一層的節點。廣度優先遍歷可以使用隊列來實現。

前序遍歷

根節點 -> 左子樹 -> 右子樹。在前序遍歷中，首先訪問根節點，然後按照左子樹和右子樹的順序遞歸地進行前序遍歷。

    // 前序遍歷二叉樹（根-左-右）
    public static void preOrderTraversal(TreeNode node) {
        if (node == null) {
            return;
        }

        System.out.print(node.val + " ");

        preOrderTraversal(node.left);
        preOrderTraversal(node.right);
    }

中序遍歷

左子樹 -> 根節點 -> 右子樹。在中序遍歷中，首先按照左子樹的順序遞歸地進行中序遍歷，然後訪問根節點，最後按照右子樹的順序遞歸地進行中序遍歷。

    // 中序遍歷二叉樹（左-根-右）
    public static void inOrderTraversal(TreeNode node) {
        if (node == null) {
            return;
        }

        inOrderTraversal(node.left);

        System.out.print(node.val + " ");

        inOrderTraversal(node.right);
    }

後序遍歷

左子樹 -> 右子樹 -> 根節點。在後序遍歷中，首先按照左子樹和右子樹的順序遞歸地進行後序遍歷，然後訪問根節點。

    // 後序遍歷二叉樹（左-右-根）
    public static void postOrderTraversal(TreeNode node) {
        if (node == null) {
            return;
        }

        postOrderTraversal(node.left);
        postOrderTraversal(node.right);

        System.out.print(node.val + " ");
    }

 public static void main(String[] args) {
        // 創建一個二叉樹
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.left.left = new TreeNode(4);
        root.left.right = new TreeNode(5);

        // 前序遍歷二叉樹
        System.out.println("前序遍歷結果：");
        preOrderTraversal(root);

        // 中序遍歷二叉樹
        System.out.println("\n中序遍歷結果：");
        inOrderTraversal(root);

        // 後序遍歷二叉樹
        System.out.println("\n後序遍歷結果：");
        postOrderTraversal(root);
    }

層次遍歷

是一種廣度優先遍歷的應用，它按照層級順序逐層訪問二叉樹的節點。在層次遍歷中，從根節點開始，先訪問根節點，然後按照從左到右的順序逐層訪問每個節點的子節點，一層一層橫向遍歷各個節點，可以藉助於隊列實現。

public static void levelOrderTraversal(TreeNode root) {
    if (root == null) {
        return;
    }
    
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root); // 將根節點入隊
    
    while (!queue.isEmpty()) {
        int levelSize = queue.size(); // 當前層級的節點數量
        
        for (int i = 0; i < levelSize; i++) {
            TreeNode node = queue.poll(); // 出隊當前節點
            System.out.print(node.val + " "); // 訪問當前節點
            
            if (node.left != null) {
                queue.offer(node.left); // 左子節點入隊
            }
            
            if (node.right != null) {
                queue.offer(node.right); // 右子節點入隊
            }
        }
        
        System.out.println(); // 換行表示進入下一層級
    }
}

存儲結構

順序結構存儲

使用數組來表示二叉樹的結構。按照層級順序依次將二叉樹節點存儲到數組中，空缺位置用特定值（如null）表示。這種存儲結構適用於完全二叉樹，因為不是完全二叉樹會有空間的浪費，可以通過數組下標計算節點之間的關係。

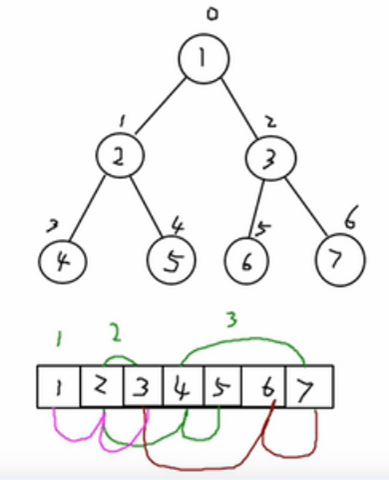
特點：

  • 順序二叉樹通常只考慮完全二叉樹

  • 第n個元素的左子節點為 2* n +1

  • 第n個元素的右子節點為 2* n + 2

  • 第n個元素的父節點為 (n-1)/2

n: 表示二又樹中的第幾個元素(按0開始編號如圖所示)

代碼示例

public class ArrayBinaryTree {
    private int[] treeArray;
    private int size;

    public ArrayBinaryTree(int capacity) {
        treeArray = new int[capacity];
        size = 0;
    }

    public void insert(int data) {
        if (size >= treeArray.length) {
            System.out.println("The tree is full");
            return;
        }

        treeArray[size] = data;
        size++;
    }

    public void inorderTraversal(int index) {
        if (index >= size) {
            return;
        }
        
        inorderTraversal(index * 2 + 1); // 訪問左子樹
        System.out.print(treeArray[index] + " "); // 訪問當前節點
        inorderTraversal(index * 2 + 2); // 訪問右子樹
    }

    public static void main(String[] args) {
        ArrayBinaryTree tree = new ArrayBinaryTree(10);
        tree.insert(1);
        tree.insert(2);
        tree.insert(3);
        tree.insert(4);
        tree.insert(5);

        System.out.print("Inorder Traversal: ");
        tree.inorderTraversal(0); // 輸出: 4 2 5 1 3
    }
}

鏈式存儲

用節點對象和指針來表示二叉樹的結構。每個節點包含一個數據元素和左右子節點的指針。用鏈表來表示一棵二叉樹，即用鏈來指示元素的邏輯關係。 通常的方法是鏈表中每個結點由三個域組成，數據域和左右指針域，左右指針分別用來給出該結點左孩子和右孩子所在的鏈結點的存儲地址 。這種存儲結構可以靈活地表示任意形狀的二叉樹。

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    public TreeNode(int val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}

線索化二叉樹

線索二叉樹是對普通二叉樹的一種擴展，它通過在空指針位置存儲指向當前節點的前驅節點和後繼節點的指針，使得二叉樹的遍歷更加方便。可以有效地減少遍歷的次數，同時也可以避免空指針的浪費。

  • n個結點的二又鏈表中含有n+1 [公式 2n-(n-1)=n+1] 個空指針域。利用二又鏈表中的空指針域，存放指向該結點在某種遍歷次序下的前驅和後繼結點的指針(這種附加的指針稱為"線索")

  • 這種加上了線索的二叉鏈表稱為線索鏈表，相應的二叉樹稱為線索二叉樹(Threaded BinaryTree)。根據線索性質的不同，線索二叉樹可分為前序線索叉樹、中序線索二叉樹和後序線索二叉樹三種

  • 一個結點的前一個結點，稱為前驅結點，一個結點的後一個結點，稱為後繼結點

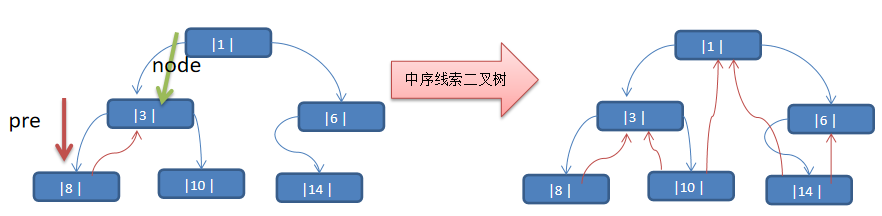
代碼實現

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    private int leftType; // 0:左子樹  1：前驅節點

    private int rightType; // 0:右子樹  1：後繼節點

    public TreeNode(int val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
    // 省略get set方法
}


class ThreadedBinaryTree {

    private TreeNode root;

    //為了實現線索化，需要創建要給指向當前結點的前驅結點的指針
    //在遞歸進行線索化時，pre 總是保留前一個結點
    private TreeNode pre = null;


    public void setRoot(TreeNode root) {
        this.root = root;
    }

    public void  threadedNodes(){
        this.threadedNodes(root);
    }

    // 線索化節點 中序線索化
    public void  threadedNodes(TreeNode node){

        if (node == null){
            return;
        }

        // 先線索化左子樹
        threadedNodes(node.getLeft());

        // 線索化當前節點
        if (node.getLeft() == null){
            //讓當前結點的左指針指向前驅結點
            node.setLeft(pre);
            node.setLeftType(1);
        }

        //處理後繼結點
        if (pre != null && pre.getRight() == null) {
            //讓前驅結點的右指針指向當前結點
            pre.setRight(node);
            //修改前驅結點的右指針類型
            pre.setRightType(1);
        }
        // 讓當前結點是下一個結點的前驅結點
        pre = node;

        pre = node;

        // 線索化右子樹
        threadedNodes(node.getRight());
    }
}

遍歷線索化二叉樹

因為線索化後，各個結點指向有變化，因此原來的遍歷方式不能使用,這時需要使用新的方式遍歷線索化二叉樹，各個節點可以通過線型方式遍歷,因此無需使用遞歸方式，這樣也提高了遍歷的效率。 遍歷的次序應當和中序遍歷保持一致。

代碼實現

    // 遍歷線索化二叉樹
    public void threadedNodeList(){
        //定義一個變數，存儲當前遍歷的結點，從root開始
        TreeNode node = root;

        while (node != null){
            while (node.getLeftType() == 0){
                node = node.getLeft();
            }

            System.out.println(node);

            while (node.getRightType() == 1){
                node = node.getRight();
                System.out.println(node);
            }
            node = node.getRight();
        }

    }

以上面圖中的例子，進行代碼測試

public class ThreadedBinaryTreeDemo {

    public static void main(String[] args) {
        TreeNode root = new TreeNode(1);
        TreeNode node2 = new TreeNode(3);
        TreeNode node3 = new TreeNode(6);
        TreeNode node4 = new TreeNode(8);
        TreeNode node5 = new TreeNode(10);
        TreeNode node6 = new TreeNode(14);

        root.setLeft(node2);
        root.setRight(node3);
        node2.setLeft(node4);
        node2.setRight(node5);
        node3.setLeft(node6);


        //測試中序線索化
        ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();
        threadedBinaryTree.setRoot(root);
        threadedBinaryTree.threadedNodes();
        //測試: 以10號節點測試
        TreeNode leftNode = node5.getLeft();
        TreeNode rightNode = node5.getRight();
        System.out.println("10號結點的前驅結點是 ="  + leftNode); //3
        System.out.println("10號結點的後繼結點是="  + rightNode); //1

        // 測試遍歷
        System.out.println("使用線索化的方式遍歷 線索化二叉樹");
        threadedBinaryTree.threadedNodeList(); // 8, 3, 10, 1, 14, 6


    }

}

您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • ArrayList/MySQL數據批量寫入Excel表格
    ArrayList/MySQL數據集合寫入Excel 1.文章概述： 寫入 Excel 文件通常需要使用一些庫或工具，而"EasyExcel"通常是指的阿裡巴巴開源的EasyExcel庫。這個庫可以讓我們在Java中簡便地進行Excel文件的讀寫操作。 2.導入配置： <dependency> <g ...
  • 試試用Markdown來設計表單
    相信很多後端開發。對於前端知識是比較零碎的，所以很多時候寫表單這樣的工作，一般就是複製黏貼，然後改改欄位。對於HTML格式，一直覺得比較雜亂，不夠簡潔。 最近TJ發現了一個有趣的小工具：Create HTML Form。 看看上面它的Slogan，是不是很有意思？居然可以通過Markdown來編寫H ...
  • python採集數據保存csv, 文件內容亂碼了怎麼解決?
    如果你的 Python 程式採集到的數據在保存成 CSV 格式的文件時出現了亂碼，那麼可嘗試以下解決方法： 1. 在打開 CSV 文件時指定編碼方式 你可以使用 Python 中的 open() 函數打開 CSV 文件，併在 open() 函數中指定文件編碼方式為 CSV 文件原始編碼方式。如果 C ...
  • 2.14 PE結構：地址之間的轉換
    在可執行文件PE文件結構中，通常我們需要用到地址轉換相關知識，PE文件針對地址的規範有三種，其中就包括了`VA`，`RVA`，`FOA`三種，這三種該地址之間的靈活轉換也是非常有用的，本節將介紹這些地址範圍如何通過編程的方式實現轉換。VA（Virtual Address，虛擬地址）：它是在進程的虛擬... ...
  • 註意避坑！Java 內部類持有外部類會導致記憶體泄露。。。
    簡介 說明 本文介紹 Java 內部類持有外部類導致記憶體泄露的原因以及其解決方案。 為什麼內部類持有外部類會導致記憶體泄露 非靜態內部類會持有外部類，如果有地方引用了這個非靜態內部類，會導致外部類也被引用，垃圾回收時無法回收這個外部類（即使外部類已經沒有其他地方在使用了）。 解決方案 不要讓其他的地方 ...
  • 平衡二叉樹（Balanced Binary Tree）
    平衡二叉樹（Balanced Binary Tree） 平衡二叉樹是一種特殊的二叉搜索樹，它具有以下特點： 每個節點的左子樹和右子樹的高度差不超過1。 所有的子樹也都是平衡二叉樹。 通過保持平衡性，平衡二叉樹可以在最壞情況下仍然具有較好的性能，保證查找、插入和刪除操作的時間複雜度為O(log n)。 ...
  • 二叉搜索樹（Binary Search Tree，BST）
    二叉搜索樹（Binary Search Tree，BST） 二叉搜索樹（Binary Search Tree），也稱二叉查找樹或二叉排序樹，是一種特殊的二叉樹，它滿足以下性質 對於二叉搜索樹的每個節點 左子樹中的所有節點的值都小於該節點的值 右子樹中的所有節點的值都大於（或等於）該節點的值 對於二叉 ...
  • Go語句與表達式深度解析：全案例手冊
    關註公眾號【TechLeadCloud】，分享互聯網架構、雲服務技術的全維度知識。作者擁有10+年互聯網服務架構、AI產品研發經驗、團隊管理經驗，同濟本復旦碩，復旦機器人智能實驗室成員，阿裡雲認證的資深架構師，項目管理專業人士，上億營收AI產品研發負責人。 語句 語句是Go編程語言中完成特定操作的單 ...
一周排行
    -Advertisement-
    Play Games
  • WPF 已知問題 監聽 WMI 事件導致觸摸失效
    示例項目結構 在 Visual Studio 中創建一個 WinForms 應用程式後，項目結構如下所示： MyWinFormsApp/ │ ├───Properties/ │ └───Settings.settings │ ├───bin/ │ ├───Debug/ │ └───Release/ ...
  • [STAThread]特性
    [STAThread] 特性用於需要與 COM 組件交互的應用程式，尤其是依賴單線程模型（如 Windows Forms 應用程式）的組件。在 STA 模式下，線程擁有自己的消息迴圈，這對於處理用戶界面和某些 COM 組件是必要的。 [STAThread] static void Main(stri ...
  • UWP WinUI3 傳入 AddHandler 的 RoutedEventHandler 類型與事件所需不匹配將拋出參數異常
    在WinForm中使用全局異常捕獲處理 在WinForm應用程式中，全局異常捕獲是確保程式穩定性的關鍵。通過在Program類的Main方法中設置全局異常處理，可以有效地捕獲並處理未預見的異常，從而避免程式崩潰。 註冊全局異常事件 [STAThread] static void Main() { / ...
  • .NET 多版本 WinForm 開源控制項庫 SunnyUI
    前言 給大家推薦一款開源的 Winform 控制項庫，可以幫助我們開發更加美觀、漂亮的 WinForm 界面。 項目介紹 SunnyUI.NET 是一個基於 .NET Framework 4.0+、.NET 6、.NET 7 和 .NET 8 的 WinForm 開源控制項庫，同時也提供了工具類庫、擴展 ...
  • .net core8 使用Swagger（附當前源碼）
    說明 該文章是屬於OverallAuth2.0系列文章，每周更新一篇該系列文章（從0到1完成系統開發）。 該系統文章，我會儘量說的非常詳細，做到不管新手、老手都能看懂。 說明：OverallAuth2.0 是一個簡單、易懂、功能強大的許可權+可視化流程管理系統。 有興趣的朋友，請關註我吧(*^▽^*) ...
  • WPF 什麼時候 VisualTreeHelper.GetDescendantBounds 將返回無窮大
    一、下載安裝 1.下載git 必須先下載並安裝git，再TortoiseGit下載安裝 git安裝參考教程：https://blog.csdn.net/mukes/article/details/115693833 2.TortoiseGit下載與安裝 TortoiseGit，Git客戶端，32/6 ...
  • C# 開源教程帶你輕鬆掌握數據結構與演算法
    前言 在項目開發過程中，理解數據結構和演算法如同掌握蓋房子的秘訣。演算法不僅能幫助我們編寫高效、優質的代碼，還能解決項目中遇到的各種難題。 給大家推薦一個支持C#的開源免費、新手友好的數據結構與演算法入門教程：Hello演算法。 項目介紹 《Hello Algo》是一本開源免費、新手友好的數據結構與演算法入門 ...
  • 第22篇 生成proto文件bat腳本
    1.生成單個Proto.bat內容 @rem Copyright 2016, Google Inc. @rem All rights reserved. @rem @rem Redistribution and use in source and binary forms, with or with ...
  • 記一次 .NET某上位機視覺程式 卡死分析
    一：背景 1. 講故事 前段時間有位朋友找到我，說他的窗體程式在客戶這邊出現了卡死，讓我幫忙看下怎麼回事？dump也生成了，既然有dump了那就上 windbg 分析吧。 二：WinDbg 分析 1. 為什麼會卡死 窗體程式的卡死，入口門檻很低，後續往下分析就不一定了，不管怎麼說先用 !clrsta ...
  • 醫學DICOM文件與PACS系統進行數據傳輸
    前言 人工智慧時代，人臉識別技術已成為安全驗證、身份識別和用戶交互的關鍵工具。 給大家推薦一款.NET 開源提供了強大的人臉識別 API，工具不僅易於集成，還具備高效處理能力。 本文將介紹一款如何利用這些API，為我們的項目添加智能識別的亮點。 項目介紹 GitHub 上擁有 1.2k 星標的 C# ...
所有分類