平衡二叉樹（Balanced Binary Tree）

来源:https://www.cnblogs.com/dupengpeng/archive/2023/09/12/17694991.html
-Advertisement-
Play Games

平衡二叉樹（Balanced Binary Tree） 平衡二叉樹是一種特殊的二叉搜索樹，它具有以下特點： 每個節點的左子樹和右子樹的高度差不超過1。 所有的子樹也都是平衡二叉樹。 通過保持平衡性，平衡二叉樹可以在最壞情況下仍然具有較好的性能，保證查找、插入和刪除操作的時間複雜度為O(log n)。 ...


平衡二叉樹（Balanced Binary Tree）

平衡二叉樹是一種特殊的二叉搜索樹，它具有以下特點：

  • 每個節點的左子樹和右子樹的高度差不超過1。
  • 所有的子樹也都是平衡二叉樹。

通過保持平衡性，平衡二叉樹可以在最壞情況下仍然具有較好的性能，保證查找、插入和刪除操作的時間複雜度為O(log n)。

平衡二叉樹的常用實現方法有紅黑樹、AVL、替罪羊樹、Treap、伸展樹等

為什麼需要平衡二叉樹

在普通的二叉搜索樹中，如果插入或刪除操作不經過特殊處理，很容易出現樹的不平衡，使得樹的高度變得很大，導致查找操作的效率下降。

平衡二叉樹通過在每次插入或刪除後調整樹的結構，保持樹的平衡性。這樣可以確保樹的高度儘可能地低，使得查找操作仍然可以在較短的時間內完成。

如下圖：左子樹全部為空，從形式上看，更像一個單鏈表

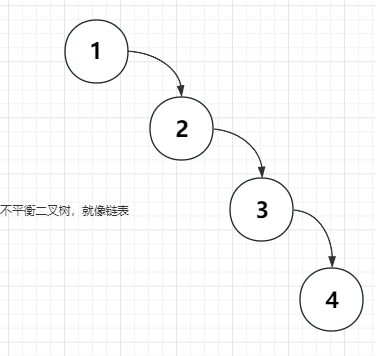
怎麼平衡樹高的呢？

當二叉樹的左右分支樹高差不為 1 時，需要進行左旋或者右旋，來調衡樹高。這有點像開車的時候，如果車頭偏左就往右打方向盤，車頭偏右就往左打方向盤是一個道理。

class AVLTree {
    private Node root;

    private class Node {
        int val;
        int height; // 增加一個樹高
        Node left;
        Node right;

        public Node(int val) {
            this.val = val;
            this.height = 1;
            this.left = null;
            this.right = null;
        }
    }
}

平衡因數

平衡因數是用來衡量平衡二叉樹中某個節點的左子樹和右子樹高度差的一個指標。它表示了節點的平衡性，可以用來判斷是否需要進行旋轉操作來恢復樹的平衡。
平衡因數的計算方法是，對於一個節點，它的平衡因數等於左子樹高度減去右子樹高度。具體公式可以表示為：
平衡因數 = 左子樹高度 - 右子樹高度
根據平衡因數的值，可以判斷節點的平衡情況：

  • 平衡因數為0： 左子樹和右子樹的高度相等，節點處於平衡狀態。
  • 平衡因數為正數： 左子樹的高度大於右子樹的高度，節點處於左重狀態。
  • 平衡因數為負數： 右子樹的高度大於左子樹的高度，節點處於右重狀態。
    當平衡因數的絕對值大於1時，表示節點的左右子樹高度差過大，樹失去平衡，需要進行旋轉操作來恢復平衡。
    通過平衡因數的判斷，可以及時發現不平衡的節點，並採取相應的調整措施以保持平衡二叉樹的平衡性，確保樹的高度在可控範圍內，從而提高查找、插入和刪除操作的效率。

左旋轉

左旋是平衡二叉樹中的一種旋轉操作，用於調整不平衡節點及其子節點之間的關係。左旋的目的是將不平衡節點向左移動，並提升其右子節點作為新的父節點，從而恢復樹的平衡性。

左旋的觸發條件是當節點A的右子樹高度較高（平衡因數大於1），並且節點B的左子樹高度不小於節點B的右子樹高度時，需要進行左旋操作。

具體情況下，左旋通常在以下情況下使用：

  1. 當在平衡二叉樹中插入一個節點後，導致某個節點的平衡因數大於1，即左子樹高度比右子樹高度多2或更多時，需要進行左旋操作。
  2. 在刪除節點後，導致某個節點的平衡因數小於-1，即右子樹高度比左子樹高度多2或更多時，也需要進行左旋操作。

左旋的目的是使得樹保持平衡，確保樹的高度差不超過1，從而保證查找、插入和刪除等操作的時間複雜度在O(log n)範圍內。

如下圖：左旋的作用，相當於通過向上遷移樹高差大於 1 的右子節點來降低樹高的操作

  1. 找到需要進行左旋的節點，即節點值為4的節點。
  2. 將節點值為6的節點提升為新的根節點，並將原來的根節點值為4的節點降級為新根節點的左子節點。
  3. 將原來新根節點值為6的右子節點（值為7）作為原來根節點的右子節點。
  4. 將6原來的左子節點作為4個右子節點
  5. 更新相關節點的高度信息。

代碼實現

    // 左旋轉操作
    private Node rotateLeft(Node x) {
        Node y = x.right;
        Node T2 = y.left;

        // 執行旋轉
        y.left = x;
        x.right = T2;

        // 更新節點高度
        x.height = Math.max(height(x.left), height(x.right)) + 1;
        y.height = Math.max(height(y.left), height(y.right)) + 1;

        return y;
    }

右旋轉

和左旋轉類似，目的是將不平衡節點向右移動，並提升其左子節點作為新的父節點，從而恢復樹的平衡性。

  1. 找到需要進行右旋的節點，即節點值為10的節點。
  2. 將節點值為8的節點提升為新的根節點，並將原來的根節點值為10的節點降級為新根節點的右子節點。
  3. 將原來新根節點值為8的左子節點（值為7）作為原來根節點的左子節點。
  4. 更新相關節點的高度信息。

代碼實現

    // 右旋轉操作
    private Node rotateRight(Node y) {
        Node x = y.left;
        Node T2 = x.right;

        // 執行旋轉
        x.right = y;
        y.left = T2;

        // 更新節點高度
        y.height = Math.max(height(y.left), height(y.right)) + 1;
        x.height = Math.max(height(x.left), height(x.right)) + 1;

        return x;
    }

左右旋（先左旋後右旋）

當某個節點的左子樹的右子樹過深，平衡因數小於-1時，需要進行左旋-右旋操作，先對左子節點進行左旋，然後再對當前節點進行右旋，如下圖


完整代碼在下麵

右左旋（先右旋後左旋）

當某個節點的右子樹的左子樹過深，平衡因數大於1時，需要進行右旋-左旋操作，先對右子節點進行右旋，然後再對當前節點進行左旋。和上面類似

完整代碼示例

public class AvlTreeDemo {
    public static void main(String[] args) {
        // 創建平衡二叉樹對象
        AVLTree avlTree = new AVLTree();
        // 插入節點
        avlTree.insert(10);
        avlTree.insert(11);
        avlTree.insert(7);
        avlTree.insert(6);
        avlTree.insert(8);
        avlTree.insert(9);
        // 中序遍歷並輸出節點值
        System.out.print("中序遍歷結果：");
        avlTree.inorderTraversal(); // 輸出：10 20 25 30 40 50
    }
}

class AVLTree {
    private Node root;

    private class Node {
        int val;
        int height;
        Node left;
        Node right;

        public Node(int val) {
            this.val = val;
            this.height = 1;
            this.left = null;
            this.right = null;
        }
    }

    // 計算節點的高度
    private int height(Node node) {
        if (node == null) {
            return 0;
        }
        return node.height;
    }

    // 計算節點的平衡因數
    private int balanceFactor(Node node) {
        if (node == null) {
            return 0;
        }
        return height(node.left) - height(node.right);
    }

    // 右旋轉操作
    private Node rotateRight(Node y) {
        Node x = y.left;
        Node T2 = x.right;

        // 執行旋轉
        x.right = y;
        y.left = T2;

        // 更新節點高度
        y.height = Math.max(height(y.left), height(y.right)) + 1;
        x.height = Math.max(height(x.left), height(x.right)) + 1;

        return x;
    }

    // 左旋轉操作
    private Node rotateLeft(Node x) {
        Node y = x.right;
        Node T2 = y.left;

        // 執行旋轉
        y.left = x;
        x.right = T2;

        // 更新節點高度
        x.height = Math.max(height(x.left), height(x.right)) + 1;
        y.height = Math.max(height(y.left), height(y.right)) + 1;

        return y;
    }

    // 插入節點
    public void insert(int val) {
        root = insertNode(root, val);
    }

    private Node insertNode(Node node, int val) {
        // 執行標準的BST插入
        if (node == null) {
            return new Node(val);
        }

        if (val < node.val) {
            node.left = insertNode(node.left, val);
        } else if (val > node.val) {
            node.right = insertNode(node.right, val);
        } else { // 如果值相等，不允許重覆插入
            return node;
        }

        // 更新節點的高度
        node.height = Math.max(height(node.left), height(node.right)) + 1;

        // 計算平衡因數
        int balance = balanceFactor(node);

        // 進行平衡調整
        // 左子樹不平衡，右旋轉
        if (balance > 1 && val < node.left.val) {
            return rotateRight(node);
        }
        // 右子樹不平衡，左旋轉
        if (balance < -1 && val > node.right.val) {
            return rotateLeft(node);
        }
        // 左子樹不平衡，先左旋轉後右旋轉
        if (balance > 1 && val > node.left.val) {
            node.left = rotateLeft(node.left);
            return rotateRight(node);
        }
        // 右子樹不平衡，先右旋轉後左旋轉
        if (balance < -1 && val < node.right.val) {
            node.right = rotateRight(node.right);
            return rotateLeft(node);
        }

        return node;
    }

    // 中序遍歷
    public void inorderTraversal() {
        inorderHelper(root);
    }

    private void inorderHelper(Node node) {
        if (node == null) {
            return;
        }
        inorderHelper(node.left);
        System.out.print(node.val + " ");
        inorderHelper(node.right);
    }

    public static void main(String[] args) {
        // 創建平衡二叉樹對象
        AVLTree avlTree = new AVLTree();

        // 插入節點
        avlTree.insert(10);
        avlTree.insert(20);
        avlTree.insert(30);
        avlTree.insert(40);
        avlTree.insert(50);
        avlTree.insert(25);

        // 中序遍歷並輸出節點值
        System.out.print("中序遍歷結果：");
        avlTree.inorderTraversal(); // 輸出：10 20 25 30 40 50
    }
}

您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • php使用jwt作登錄驗證
    JWT官網 https://jwt.io/ 選擇第一個 composer require firebase/php-jwt use Firebase\JWT\ExpiredException;use Firebase\JWT\JWT;use Firebase\JWT\Key;use Firebase ...
  • Go學習筆記5
    在今天的移動互聯網時代，手機已經成為了人們不可或缺的重要工具，而手機的聯網狀態也是我們經常需要關註的一個問題。我們需要保證手機網路處於正常的連接狀態，但是有時候，由於種種原因，手機的網路可能會斷開，這時我們需要及時發現，併進行相應的處理措施。而利用Api介面實現手機網路連接斷開的監聽，便是一種較為高 ...
  • 什麼是方法重載？返回值算重載嗎？
    遞歸函數和其他拓展 課前練習 請實現一個裝飾器，把'函數的返回值'+100然後'返回' def ount(fun): def werrod(*ardes,**warrrts): res=fun(*ardes,**warrrts) return res+100 return werrod @ount ...
  • ArrayList/MySQL數據批量寫入Excel表格
    ArrayList/MySQL數據集合寫入Excel 1.文章概述： 寫入 Excel 文件通常需要使用一些庫或工具，而"EasyExcel"通常是指的阿裡巴巴開源的EasyExcel庫。這個庫可以讓我們在Java中簡便地進行Excel文件的讀寫操作。 2.導入配置： <dependency> <g ...
  • 試試用Markdown來設計表單
    相信很多後端開發。對於前端知識是比較零碎的，所以很多時候寫表單這樣的工作，一般就是複製黏貼，然後改改欄位。對於HTML格式，一直覺得比較雜亂，不夠簡潔。 最近TJ發現了一個有趣的小工具：Create HTML Form。 看看上面它的Slogan，是不是很有意思？居然可以通過Markdown來編寫H ...
  • python採集數據保存csv, 文件內容亂碼了怎麼解決?
    如果你的 Python 程式採集到的數據在保存成 CSV 格式的文件時出現了亂碼，那麼可嘗試以下解決方法： 1. 在打開 CSV 文件時指定編碼方式 你可以使用 Python 中的 open() 函數打開 CSV 文件，併在 open() 函數中指定文件編碼方式為 CSV 文件原始編碼方式。如果 C ...
  • 2.14 PE結構：地址之間的轉換
    在可執行文件PE文件結構中，通常我們需要用到地址轉換相關知識，PE文件針對地址的規範有三種，其中就包括了`VA`，`RVA`，`FOA`三種，這三種該地址之間的靈活轉換也是非常有用的，本節將介紹這些地址範圍如何通過編程的方式實現轉換。VA（Virtual Address，虛擬地址）：它是在進程的虛擬... ...
  • 註意避坑！Java 內部類持有外部類會導致記憶體泄露。。。
    簡介 說明 本文介紹 Java 內部類持有外部類導致記憶體泄露的原因以及其解決方案。 為什麼內部類持有外部類會導致記憶體泄露 非靜態內部類會持有外部類，如果有地方引用了這個非靜態內部類，會導致外部類也被引用，垃圾回收時無法回收這個外部類（即使外部類已經沒有其他地方在使用了）。 解決方案 不要讓其他的地方 ...
一周排行
    -Advertisement-
    Play Games
  • WPF 已知問題 監聽 WMI 事件導致觸摸失效
    示例項目結構 在 Visual Studio 中創建一個 WinForms 應用程式後，項目結構如下所示： MyWinFormsApp/ │ ├───Properties/ │ └───Settings.settings │ ├───bin/ │ ├───Debug/ │ └───Release/ ...
  • [STAThread]特性
    [STAThread] 特性用於需要與 COM 組件交互的應用程式，尤其是依賴單線程模型（如 Windows Forms 應用程式）的組件。在 STA 模式下，線程擁有自己的消息迴圈，這對於處理用戶界面和某些 COM 組件是必要的。 [STAThread] static void Main(stri ...
  • UWP WinUI3 傳入 AddHandler 的 RoutedEventHandler 類型與事件所需不匹配將拋出參數異常
    在WinForm中使用全局異常捕獲處理 在WinForm應用程式中，全局異常捕獲是確保程式穩定性的關鍵。通過在Program類的Main方法中設置全局異常處理，可以有效地捕獲並處理未預見的異常，從而避免程式崩潰。 註冊全局異常事件 [STAThread] static void Main() { / ...
  • .NET 多版本 WinForm 開源控制項庫 SunnyUI
    前言 給大家推薦一款開源的 Winform 控制項庫，可以幫助我們開發更加美觀、漂亮的 WinForm 界面。 項目介紹 SunnyUI.NET 是一個基於 .NET Framework 4.0+、.NET 6、.NET 7 和 .NET 8 的 WinForm 開源控制項庫，同時也提供了工具類庫、擴展 ...
  • .net core8 使用Swagger（附當前源碼）
    說明 該文章是屬於OverallAuth2.0系列文章，每周更新一篇該系列文章（從0到1完成系統開發）。 該系統文章，我會儘量說的非常詳細，做到不管新手、老手都能看懂。 說明：OverallAuth2.0 是一個簡單、易懂、功能強大的許可權+可視化流程管理系統。 有興趣的朋友，請關註我吧(*^▽^*) ...
  • WPF 什麼時候 VisualTreeHelper.GetDescendantBounds 將返回無窮大
    一、下載安裝 1.下載git 必須先下載並安裝git，再TortoiseGit下載安裝 git安裝參考教程：https://blog.csdn.net/mukes/article/details/115693833 2.TortoiseGit下載與安裝 TortoiseGit，Git客戶端，32/6 ...
  • C# 開源教程帶你輕鬆掌握數據結構與演算法
    前言 在項目開發過程中，理解數據結構和演算法如同掌握蓋房子的秘訣。演算法不僅能幫助我們編寫高效、優質的代碼，還能解決項目中遇到的各種難題。 給大家推薦一個支持C#的開源免費、新手友好的數據結構與演算法入門教程：Hello演算法。 項目介紹 《Hello Algo》是一本開源免費、新手友好的數據結構與演算法入門 ...
  • 第22篇 生成proto文件bat腳本
    1.生成單個Proto.bat內容 @rem Copyright 2016, Google Inc. @rem All rights reserved. @rem @rem Redistribution and use in source and binary forms, with or with ...
  • 記一次 .NET某上位機視覺程式 卡死分析
    一：背景 1. 講故事 前段時間有位朋友找到我，說他的窗體程式在客戶這邊出現了卡死，讓我幫忙看下怎麼回事？dump也生成了，既然有dump了那就上 windbg 分析吧。 二：WinDbg 分析 1. 為什麼會卡死 窗體程式的卡死，入口門檻很低，後續往下分析就不一定了，不管怎麼說先用 !clrsta ...
  • 醫學DICOM文件與PACS系統進行數據傳輸
    前言 人工智慧時代，人臉識別技術已成為安全驗證、身份識別和用戶交互的關鍵工具。 給大家推薦一款.NET 開源提供了強大的人臉識別 API，工具不僅易於集成，還具備高效處理能力。 本文將介紹一款如何利用這些API，為我們的項目添加智能識別的亮點。 項目介紹 GitHub 上擁有 1.2k 星標的 C# ...
所有分類