平衡樹

平衡樹就是為了實現一類元素線上性結構中動態變化的功能所需要的數據結構。

平衡樹是一種基於二叉搜索樹的數據結構。
滿足:左兒子 \(<\) 根 \(<\) 右兒子。
也就是一切小於根節點的在左邊，一切大於根節點的在右邊。
這樣想要查找一個節點的位置時間複雜度就是 \(O(\log n)\)。

平衡樹主要有三種：Splay，fhq_Treap，Treap。
我這次主要講前兩種。
當然還有其他的像替罪羊樹，紅黑色。

Splay

Splay 是 LCT 的基礎操作。
本人以為還是 Splay 比較好理解的。

核心操作

Splay 的基本操作就是將BST旋轉，分左旋和右旋(其實都差不多)。
旋轉的要求：在不改變原有的中序遍歷的前提下改變樹的結構。
簡化一下：把兒子節點與父親節點的身份互換，且有BST性質。

旋轉 \(zig(x)\),\(zag(x)\) 如下圖：

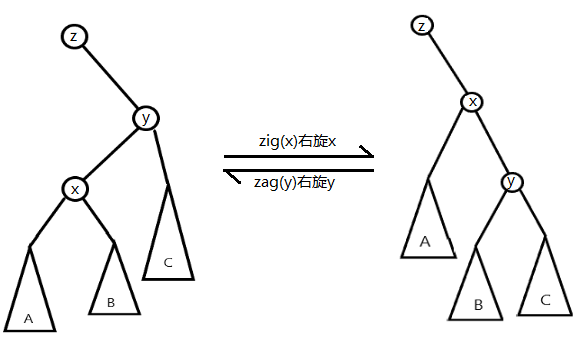
具體描述

設要旋轉的節點為 \(x\)，它的父親為 \(y\)，\(y\) 的父親為 \(z\)。

• 將 \(y\) 的左兒子設為 \(x\) 的右兒子
• 若 \(x\) 的右兒子存在，將 \(x\) 的右兒子的父親設為 \(y\)
• 將 \(x\) 的右兒子設為 \(y\)
• 將 \(y\) 的父親設為 \(x\)
• 將 \(x\) 的父親設為 \(z\)
• 若 \(z\) 存在，將 \(z\) 的某個子節點（原來 \(y\) 所在的子節點）設為 \(x\)

雙旋操作

在 Splay 中，每加入一個新的節點就需要把它旋轉到根。
設當前需旋轉的節點為 \(x\)，節點的旋轉可分為以下三種：
\(1.\)\(x\) 的父親是根，這時直接旋轉即可。
\(2.\)父親和 \(x\) 的兒子同側（即同為左兒子或同為右兒子），這時先旋轉父親，再旋轉 \(x\)。
\(3.\)父親和 \(x\) 的兒子不同側，這時將 \(x\) 旋轉兩次。
如下圖：

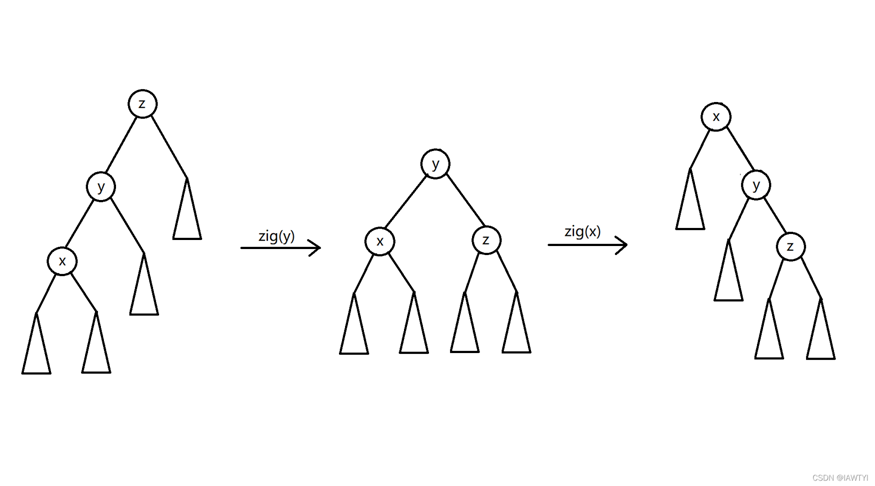
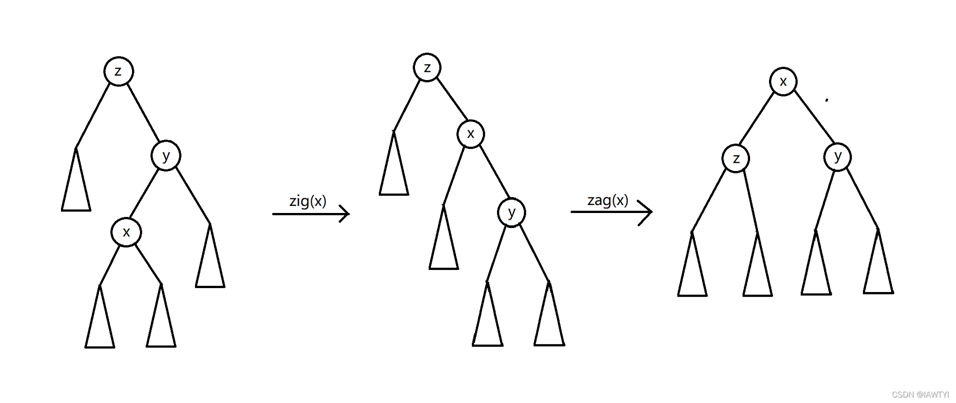
時間複雜度

對於這個時間複雜度的分析，我們需要用一下勢能分析。
設\(siz(x)\) 表示以 \(x\) 為根節點的子樹大小。
\(\phi(x)\) 表示在進行 \(x\) 次操作後的勢能函數。
\(c(x)\) 表示時間的時間複雜度。
\(a(x)\) 表示均攤的時間複雜度。
所以根據定義，我們可以得出：
\(\phi(x)=\log(siz(x))\)
\(a(x)=c(x)+\phi(x)-\phi(x-1)\)
即 \(\sum a(x)=\phi(n)-\phi(0)+\sum c(x)\)
因為根據 \(\phi(x)=\log(siz(x))\)，所以現在肯定有:\(|\phi(n)-\phi(0)|\le n\log n\)
考慮每一次的 \(\Delta\phi\)

對於zig:

對於zig-zig

那麼Splay到根的均攤代價為 \(O(logn)\)，\(zig\) 只有一次操作，所以只會使均攤代價增加\(k\)
再算上 \(\phi(n)-\phi(0)=n\log n\)
所以總時間複雜度為 \(O(n\log n)\)。

操作實現

講了核心操作和時間複雜度後，我們來看看它可以支持的操作。
註：由於我們只能保證 Splay 本身的時間複雜度，所以我們就必須只能通過旋轉來實現一些操作。

查詢數值

給定一個數 \(k\)，查詢排名為 \(k\) 的數。

• 若 \(k\) 小於等於左子樹大小，就向左子樹走
• 否則，將 \(k\) 先減去左子樹大小和當前節點的 \(cnt\)，使得 \(k\), 等於在右子樹中的排名。然而若 \(k\) 小於等於 \(0\)，說明已經找到，進行旋轉，並返回當前節點權值。

查詢 \(x\) 的前驅和後繼

我們先將 \(x\) 節點旋轉到根節點。

• 前驅：就是 \(x\) 左子樹中最右邊的節點。
• 後繼：就是 \(x\) 右子樹中最左邊的節點。

刪除節點 \(x\)

我們需要先將 \(x\) 旋轉到根節點，從而去得到它的前驅和後繼。
然後將前驅旋轉到根，再將後繼旋轉到根，就會得到下圖：

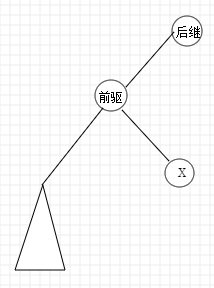
直接把 \(x\) 刪去即可。

查詢區間 \(\left[l,r\right]\)

我們需要將 \(l\) 的前驅旋轉到根，再將 \(r\) 的後繼旋轉到根節點，點像刪除操作。
而 \(l\) 前驅的右子樹就是整個 \([l,r]\) 區間了。

fhq_Treap(無旋Treap)

前言

首先，我們要 \(sto\) 範浩強 \(orz\)。
dalao 發明瞭 fhq_Treap，因為 fhq_Treap 是三種平衡樹中最強悍的一種了，它可以維護值域，可以維護下標，可以維護區間修改，它還可以完成可持久化操作。其唯一弱於 splay 的就是在維護 LCT 上。

什麼是 fhq_Treap

fhp_Treap 首先是一個 Treap。
而 Treap 是什麼呢
Treap=BST+Heap。
所以 Treap 就是一個擁有二叉搜索樹的性質，但是每一個節點都通過一個附加權值來滿足符合堆的性質。
而這個附加權值就是 Treap 的一個關鍵，它是通過隨機生成一個 \(key\) 來維護一個近似的平衡。
而我們隨機生成的 \(key\) 要想讓它退化成鏈的概率是微乎其微的。(教練：你讓隨機 \(key\) 退化成鏈的概率就像你出門被核彈直接創死的概率一樣小。)
但是一個旋轉的 Treap 是有點噁心的。
所以，我們的無旋 Treap 就登場了。

核心操作

我們要想 Treap 不旋轉，我們就需要一個可以頂替旋轉的一種操作來實現，那就是拆分與合併。

split

split 就是把 Treap 以 \(k\) 值分為兩棵 Treap。
對於我們遍歷到每一個點，假如它的權值小於 \(k\)，那麼它的左子樹，就要分到左子樹里，然後再遍歷它的右兒子，反之亦然。
因為它的最多操作次數就是一直分到底，時間複雜度就是 \(O(\log n)\)。
對於前 \(k\) 個版的，就像找第 \(k\) 大的感覺。每次減掉 \(siz\)。
這個用遞歸就可以實現了。

merge

merge 就是把被分開的兩顆 Treap 合併起來。
因為第一個 Treap 的權值都比較小，我們比較一下它的 \(kay\)，假如第一個的 \(key\) 小，我們就可以直接保留它的所有左子樹，再把第二個 Treap 變成它的右兒子，反之亦然。
也就是說，我們其實是遍歷了第一個 Treap 的根定為最大節點，第二個 Treap 的根就是最小節點，時間複雜度就是 \(O(\log n)\) 了。

操作實現

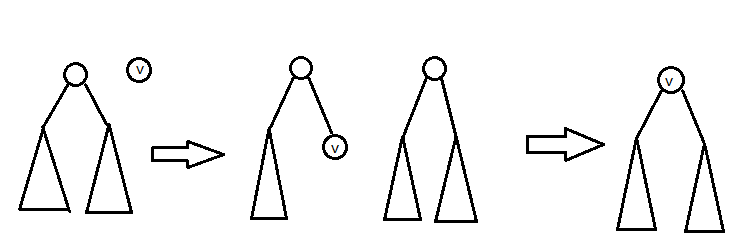
插入數值

插入一個權值為 \(v\) 的點。

• 把 Treap 以權值 \(v\) 分成兩顆。
• 將權值 \(v\) 插入。
• 再把兩顆 Treap 合併以來。
  

刪除數值

刪除一個權值為 \(v\) 的點，很類似於插入操作。

• 把 Treap 以權值 \(v\) 分成兩顆。
• 將權值 \(v\) 刪去。
• 再把兩顆 Treap 合併以來。

查詢指定值的排名

如果是在一個有序的序列中查詢排名，我們可以二分查找這個序列，然後根據找到的元素的下標來確定排名，假設下標從 \(1\) 開始，那麼排名就為該元素的下標 \(i\)。那麼，在它之前，也就有 \(i−1\) 個元素。由此，我們可以得到排名的一種定義：在有序序列中，一個元素的排名就是它前面的元素的個數 \(+1\)。
在 fhq_Treap 上，我們就直接按 \(key−1\) 分裂樹，查一下值小於等於 \(key−1\) 的樹的大小，再 \(+1\) 即可。

總結

平衡樹大體就利用 BST 性質，通過一些如旋轉，分裂合併的操作來實現將我們需要進行修改的節點或子樹獨立出來，在進行修改。