什麼是主席樹

主席樹這個名字看上去很高級，其實不然，它還有另一個名字——可持久化線段樹。

什麼是可持久化

可持久化顧名思義就是它可以變得持久，就是我們對他不斷進行單點修改後，突然查詢它的某一個歷史版本，這就叫可持久化。

引入例題

洛谷3919:可持久化數組

題目大意

如題，你需要維護這樣的一個長度為 \(N\ (1\le N\le 10^6)\) 的數組，支持如下幾種操作

• 1.在某個歷史版本上修改某一個位置上的值

• 2.訪問某個歷史版本上的某一位置的值

此外，每進行一次操作（對於操作 2，即為生成一個完全一樣的版本，不作任何改動），就會生成一個新的版本。版本編號即為當前操作的編號（從 1 開始編號，版本 0 表示初始狀態數組）

此時我們就需要用到主席樹了。

分析

問題：這裡我們為什麼能直接用數組來做？

很簡單，如何我們用數組來做的話每改變一個數，我們就要新建一個數組並將其他沒有改變的也一起複制下來，而\(1\le N \le 10^6\) 空間不支持。（如果可以就沒必要做了）

思考：問什麼明明只修改了一個數，卻必須將其他的數也複製一遍？

那是因為數組的一級索引所決定的。

什麼是索引

索引是一種單獨的、物理的對資料庫表中一列或多列的值進行排序的一種存儲結構，它是某個表中一列或若幹列值的集合和相應的指向表中物理標識這些值的數據頁的邏輯指針清單。

索引的作用相當於圖書的目錄，可以根據目錄中的頁碼快速找到所需的內容。

最優索引

問題：怎樣的索引是最高效呢？

這裡，我們設索引大小為 \(k\),那麼索引的層數為 \(\log_kn\),則每次修改的數量為 \(k\log_kn\)。

\(k\log_kn=\log_kn^k=k\dfrac{\log n}{\log k}=\log n\dfrac{k}{\log k}\)

設\(f(n)=\dfrac{k}{\log k}\)

\(f'(n)=\dfrac{\log k+1}{\log^2 k}=\left(\dfrac{1}{\log k}\right)^2+\dfrac{1}{\log k}\)

在 \(1\le k\le n\) 的情況下，\(\log k\in\left[0,\infty\right]\)。

所以 \(k_{\min}=e\ (\log k=1)\)。

即索引為 \(k=2\) 或 \(k=3\) 時最優。

這裡我們取 \(k=2\),因為它可以用線段樹維護。

演算法

原理

我們想要支持回退操作就需要對每一次修改操作都進行一次複製，將一些未進行操作也進行複製，這樣就可以訪問到舊版本的線段樹了。

那我們來分析一下單點修改時那些需要複製：

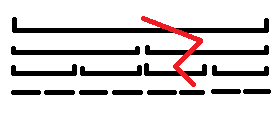
所以每一次修改我們只需要修改 \(\log n\) 個點，像這樣：

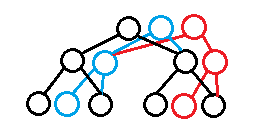
每一次都只修改被影響的點就可以。

從這張圖中，我們就發現主席樹的一些性質：

• 增加的非葉結點的兒子一個是其他版本的節點，一個是新節點。

• 主席樹有很多根

• 對於每一個根下麵都是一棵完整的線段樹

• 節點都有可能有很多父節點

具體實現

• 每次增加新節點直接開一塊空間新節點，編號為總節點數個數+1

• 用結構體來存子節點編號

• 訪問子節點時，不是像線段樹一樣乘2或乘2+1，而是在結構體存子節點編號

• 每次新開個數組存根。

模版代碼(P3919)

#include<bits/stdc++.h>
#define Mod 1000000007
#define int long long
#define For(i,j,k) for(int i=j;i<=k;++i)
#define FOR(i,j,k) for(int i=j;i>=k;i--)
#define mid ((l+r)>>1)
#define N 1000006
using namespace std;
int a[N],n,m,Q,root[N<<5];
struct PST{
	int lc[N<<5],rc[N<<5],val[N<<5],cnt;
	void build(int &x,int l,int r){
		x=++cnt;
		if(l==r){
			val[x]=a[l];
			return ;
		}
		build(lc[x],l,mid);
		build(rc[x],mid+1,r);
	}
	void ins(int &x,int k,int l,int r,int L,int R){
		x=++cnt;
		lc[x]=lc[k];
		rc[x]=rc[k];
		val[x]=val[k];
		if(l==r){
			val[x]=R;
			return ;
		}
		if(L<=mid)ins(lc[x],lc[k],l,mid,L,R);
		else ins(rc[x],rc[k],mid+1,r,L,R);
	}
	int query(int x,int l,int r,int k){
		if(l==r)return val[x];
		if(k<=mid)return query(lc[x],l,mid,k);
		else return query(rc[x],mid+1,r,k);
	}
}T;
signed main(){
	cin>>n>>m;
	For(i,1,n)cin>>a[i];
	T.build(root[0],1,n);
	For(i,1,m){
		int k,opt,x,y;
		cin>>k>>opt>>x;
		if(opt==1){
			cin>>y;
			T.ins(root[i],root[k],1,n,x,y);
		}
		if(opt==2){
			cout<<T.query(root[k],1,n,x)<<endl;
			root[i]=root[k];
		}
	}
	return 0;
}