使用 Go 語言實現二叉搜索樹

原文鏈接： 使用 Go 語言實現二叉搜索樹

二叉樹是一種常見並且非常重要的數據結構，在很多項目中都能看到二叉樹的身影。

它有很多變種，比如紅黑樹，常被用作 std::map 和 std::set 的底層實現；B 樹和 B+ 樹，廣泛應用於資料庫系統中。

本文要介紹的二叉搜索樹用的也很多，比如在開源項目 go-zero 中，就被用來做路由管理。

這篇文章也算是一篇前導文章，介紹一些必備知識，下一篇再來介紹具體在 go-zero 中的應用。

二叉搜索樹的特點

最重要的就是它的有序性，在二叉搜索樹中，每個節點的值都大於其左子樹中的所有節點的值，並且小於其右子樹中的所有節點的值。

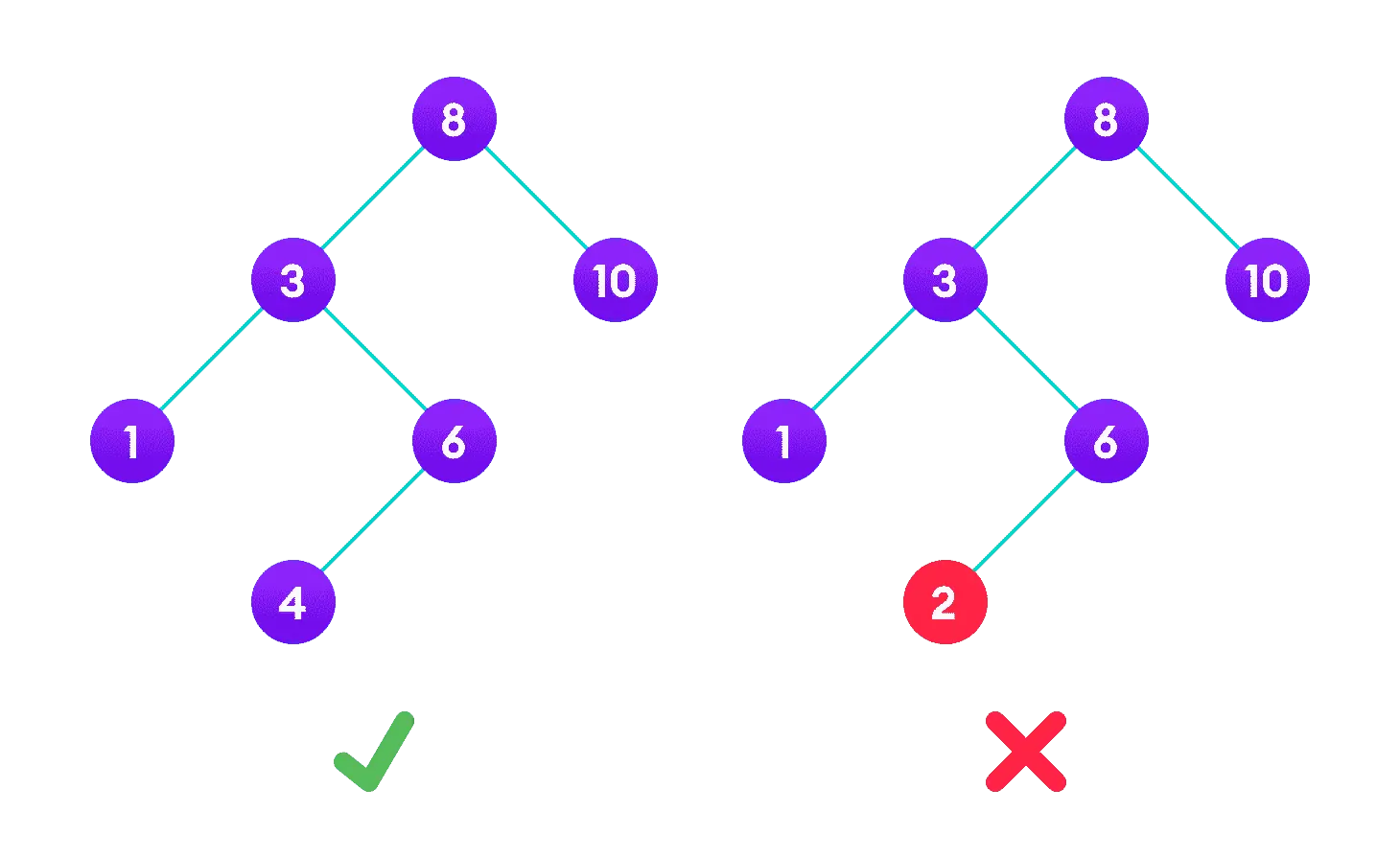
這意味著通過二叉搜索樹可以快速實現對數據的查找和插入。

Go 語言實現

本文主要實現了以下幾種方法：

• Insert(t)：插入一個節點
• Search(t)：判斷節點是否在樹中
• InOrderTraverse()：中序遍歷
• PreOrderTraverse()：前序遍歷
• PostOrderTraverse()：後序遍歷
• Min()：返回最小值
• Max()：返回最大值
• Remove(t)：刪除一個節點
• String()：列印一個樹形結構

下麵分別來介紹，首先定義一個節點：

type Node struct {
    key   int
    value Item
    left  *Node //left
    right *Node //right
}

定義樹的結構體，其中包含了鎖，是線程安全的：

type ItemBinarySearchTree struct {
    root *Node
    lock sync.RWMutex
}

插入操作：

func (bst *ItemBinarySearchTree) Insert(key int, value Item) {
    bst.lock.Lock()
    defer bst.lock.Unlock()
    n := &Node{key, value, nil, nil}
    if bst.root == nil {
        bst.root = n
    } else {
        insertNode(bst.root, n)
    }
}

// internal function to find the correct place for a node in a tree
func insertNode(node, newNode *Node) {
    if newNode.key < node.key {
        if node.left == nil {
            node.left = newNode
        } else {
            insertNode(node.left, newNode)
        }
    } else {
        if node.right == nil {
            node.right = newNode
        } else {
            insertNode(node.right, newNode)
        }
    }
}

在插入時，需要判斷插入節點和當前節點的大小關係，保證搜索樹的有序性。

中序遍歷：

func (bst *ItemBinarySearchTree) InOrderTraverse(f func(Item)) {
    bst.lock.RLock()
    defer bst.lock.RUnlock()
    inOrderTraverse(bst.root, f)
}

// internal recursive function to traverse in order
func inOrderTraverse(n *Node, f func(Item)) {
    if n != nil {
        inOrderTraverse(n.left, f)
        f(n.value)
        inOrderTraverse(n.right, f)
    }
}

前序遍歷：

func (bst *ItemBinarySearchTree) PreOrderTraverse(f func(Item)) {
    bst.lock.Lock()
    defer bst.lock.Unlock()
    preOrderTraverse(bst.root, f)
}

// internal recursive function to traverse pre order
func preOrderTraverse(n *Node, f func(Item)) {
    if n != nil {
        f(n.value)
        preOrderTraverse(n.left, f)
        preOrderTraverse(n.right, f)
    }
}

後序遍歷：

func (bst *ItemBinarySearchTree) PostOrderTraverse(f func(Item)) {
    bst.lock.Lock()
    defer bst.lock.Unlock()
    postOrderTraverse(bst.root, f)
}

// internal recursive function to traverse post order
func postOrderTraverse(n *Node, f func(Item)) {
    if n != nil {
        postOrderTraverse(n.left, f)
        postOrderTraverse(n.right, f)
        f(n.value)
    }
}

返回最小值：

func (bst *ItemBinarySearchTree) Min() *Item {
    bst.lock.RLock()
    defer bst.lock.RUnlock()
    n := bst.root
    if n == nil {
        return nil
    }
    for {
        if n.left == nil {
            return &n.value
        }
        n = n.left
    }
}

由於樹的有序性，想要得到最小值，一直向左查找就可以了。

返回最大值：

func (bst *ItemBinarySearchTree) Max() *Item {
    bst.lock.RLock()
    defer bst.lock.RUnlock()
    n := bst.root
    if n == nil {
        return nil
    }
    for {
        if n.right == nil {
            return &n.value
        }
        n = n.right
    }
}

查找節點是否存在：

func (bst *ItemBinarySearchTree) Search(key int) bool {
    bst.lock.RLock()
    defer bst.lock.RUnlock()
    return search(bst.root, key)
}

// internal recursive function to search an item in the tree
func search(n *Node, key int) bool {
    if n == nil {
        return false
    }
    if key < n.key {
        return search(n.left, key)
    }
    if key > n.key {
        return search(n.right, key)
    }
    return true
}

刪除節點：

func (bst *ItemBinarySearchTree) Remove(key int) {
    bst.lock.Lock()
    defer bst.lock.Unlock()
    remove(bst.root, key)
}

// internal recursive function to remove an item
func remove(node *Node, key int) *Node {
    if node == nil {
        return nil
    }
    if key < node.key {
        node.left = remove(node.left, key)
        return node
    }
    if key > node.key {
        node.right = remove(node.right, key)
        return node
    }
    // key == node.key
    if node.left == nil && node.right == nil {
        node = nil
        return nil
    }
    if node.left == nil {
        node = node.right
        return node
    }
    if node.right == nil {
        node = node.left
        return node
    }
    leftmostrightside := node.right
    for {
        //find smallest value on the right side
        if leftmostrightside != nil && leftmostrightside.left != nil {
            leftmostrightside = leftmostrightside.left
        } else {
            break
        }
    }
    node.key, node.value = leftmostrightside.key, leftmostrightside.value
    node.right = remove(node.right, node.key)
    return node
}

刪除操作會複雜一些，分三種情況來考慮：

1. 如果要刪除的節點沒有子節點，只需要直接將父節點中，指向要刪除的節點指針置為 nil 即可
2. 如果刪除的節點只有一個子節點，只需要更新父節點中，指向要刪除節點的指針，讓它指向刪除節點的子節點即可
3. 如果刪除的節點有兩個子節點，我們需要找到這個節點右子樹中的最小節點，把它替換到要刪除的節點上。然後再刪除這個最小節點，因為最小節點肯定沒有左子節點，所以可以應用第二種情況刪除這個最小節點即可

最後是一個列印樹形結構的方法，在實際項目中其實並沒有實際作用：

func (bst *ItemBinarySearchTree) String() {
    bst.lock.Lock()
    defer bst.lock.Unlock()
    fmt.Println("------------------------------------------------")
    stringify(bst.root, 0)
    fmt.Println("------------------------------------------------")
}

// internal recursive function to print a tree
func stringify(n *Node, level int) {
    if n != nil {
        format := ""
        for i := 0; i < level; i++ {
            format += "       "
        }
        format += "---[ "
        level++
        stringify(n.left, level)
        fmt.Printf(format+"%d\n", n.key)
        stringify(n.right, level)
    }
}

單元測試

下麵是一段測試代碼：

func fillTree(bst *ItemBinarySearchTree) {
    bst.Insert(8, "8")
    bst.Insert(4, "4")
    bst.Insert(10, "10")
    bst.Insert(2, "2")
    bst.Insert(6, "6")
    bst.Insert(1, "1")
    bst.Insert(3, "3")
    bst.Insert(5, "5")
    bst.Insert(7, "7")
    bst.Insert(9, "9")
}

func TestInsert(t *testing.T) {
    fillTree(&bst)
    bst.String()

    bst.Insert(11, "11")
    bst.String()
}

// isSameSlice returns true if the 2 slices are identical
func isSameSlice(a, b []string) bool {
    if a == nil && b == nil {
        return true
    }
    if a == nil || b == nil {
        return false
    }
    if len(a) != len(b) {
        return false
    }
    for i := range a {
        if a[i] != b[i] {
            return false
        }
    }
    return true
}

func TestInOrderTraverse(t *testing.T) {
    var result []string
    bst.InOrderTraverse(func(i Item) {
        result = append(result, fmt.Sprintf("%s", i))
    })
    if !isSameSlice(result, []string{"1", "2", "3", "4", "5", "6", "7", "8", "9", "10", "11"}) {
        t.Errorf("Traversal order incorrect, got %v", result)
    }
}

func TestPreOrderTraverse(t *testing.T) {
    var result []string
    bst.PreOrderTraverse(func(i Item) {
        result = append(result, fmt.Sprintf("%s", i))
    })
    if !isSameSlice(result, []string{"8", "4", "2", "1", "3", "6", "5", "7", "10", "9", "11"}) {
        t.Errorf("Traversal order incorrect, got %v instead of %v", result, []string{"8", "4", "2", "1", "3", "6", "5", "7", "10", "9", "11"})
    }
}

func TestPostOrderTraverse(t *testing.T) {
    var result []string
    bst.PostOrderTraverse(func(i Item) {
        result = append(result, fmt.Sprintf("%s", i))
    })
    if !isSameSlice(result, []string{"1", "3", "2", "5", "7", "6", "4", "9", "11", "10", "8"}) {
        t.Errorf("Traversal order incorrect, got %v instead of %v", result, []string{"1", "3", "2", "5", "7", "6", "4", "9", "11", "10", "8"})
    }
}

func TestMin(t *testing.T) {
    if fmt.Sprintf("%s", *bst.Min()) != "1" {
        t.Errorf("min should be 1")
    }
}

func TestMax(t *testing.T) {
    if fmt.Sprintf("%s", *bst.Max()) != "11" {
        t.Errorf("max should be 11")
    }
}

func TestSearch(t *testing.T) {
    if !bst.Search(1) || !bst.Search(8) || !bst.Search(11) {
        t.Errorf("search not working")
    }
}

func TestRemove(t *testing.T) {
    bst.Remove(1)
    if fmt.Sprintf("%s", *bst.Min()) != "2" {
        t.Errorf("min should be 2")
    }
}

上文中的全部源碼都是經過測試的，可以直接運行，並且已經上傳到了 GitHub，需要的同學可以自取。

以上就是本文的全部內容，如果覺得還不錯的話歡迎點贊，轉發和關註，感謝支持。

源碼地址：

• https://github.com/yongxinz/go-example

推薦閱讀：

• Go 語言 select 都能做什麼？
• Go 語言 context 都能做什麼？

參考文章：

• https://flaviocopes.com/golang-data-structure-binary-search-tree/