# 尾碼數組是什麼 尾碼數組就是主要處理字元串尾碼問題的,它的實現演算法主要有兩種:倍增法和 DC3,複雜度分別是 $O(n\log n)$ 和 $O(n)$。這裡由於 DC3 代碼答辯且難以理解,我就只寫了倍增法的實現。 # 例題引入 [P3809 【模板】尾碼排序](https://www.luo ...
尾碼數組是什麼
尾碼數組就是主要處理字元串尾碼問題的,它的實現演算法主要有兩種:倍增法和 DC3,複雜度分別是 \(O(n\log n)\) 和 \(O(n)\)。這裡由於 DC3 代碼答辯且難以理解,我就只寫了倍增法的實現。
例題引入
題目大意
讀入一個長度為 \(n\) 的由大小寫英文字母或數字組成的字元串,把這個字元串的所有非空尾碼按字典序從小到大排序,然後按順序輸出尾碼的第一個字元在原串中的位置。位置編號為 \(1\) 到 \(n\)。
前置芝士
演算法
尾碼數組記錄的就是字元串第 \(i\) 個尾碼的排名。
比如一個字元串 \(S=abaababa\) 的尾碼就是:

如果我們暴力去提取出 \(S\) 的所有尾碼在給它排序顯然是不行的,因為它的時間複雜度是 \(O(n^2\log n)\) 的。
倍增法
既然單純的暴力不行,我們就需要考慮用倍增來處理。
倍增法的主要思想是:
每次將所有尾碼按照前 \(2^k\) 個字元排序,最後得出所有尾碼的排序。
這樣問題就轉化為了:現在已知所有尾碼關於前 \(2^{k−1}\) 個字元的排序,要對所有尾碼排序按前 \(2^k\) 個字元排序。
那麼我們就可以將前 \(2^k\) 個字元分為兩部分,每一部分的長度都是 \(2^{k−1}\),並且這兩部分按照字典序排序後的名次是已知的。
這裡我們定義前一部分的排名為第一關鍵字 \(key1\),後一部分的排名為第二關鍵字 \(key2\)。然後每次按照關鍵字進行排序,更新 \(rank\) 數組,得到新的排名。
這就是倍增法對尾碼數組的處理,比如當處理 \(S=aabaaaab\) 時過程如圖:
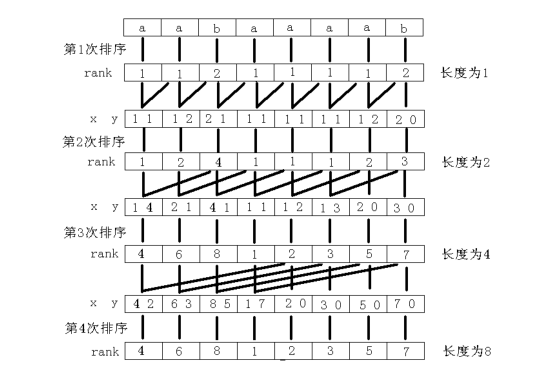
註意,這裡處理第一第二關鍵字排序時,需要先按第一關鍵字的大小排序,再用第二關鍵字來排,其思想與基數排序很像。
由於字元串的每個尾碼都是不同的(至少長度不同),所以最後得到的 \(rank\) 數組裡的數必定是互不相同的。同樣,如果再做第 \(k\) 次倍增時,得到的 \(rank\) 數組如果已經互不相同了,那麼就說明已經找到了最終的 \(rank\) 數組,可以直接退出迴圈了。
實現方法
要想通過倍增法求出尾碼數組有兩種排序方法。
快速排序 \(O(n\log ^2n)\)
用快速排序來做倍增法是很直觀,有助於初學者更好地理解尾碼數組-倍增法的思路,代碼也很簡單。
Code
#include<bits/stdc++.h>
#define int long long
#define N 1000005
#define Mod 1000000007
#define For(i,j,k) for(long long i=j;i<=k;++i)
#define FoR(i,j,k) for(long long i=j;i<k;++i)
#define FOR(i,j,k) for(long long i=j;i>=k;--i)
using namespace std;
struct Node{
int key1,key2,i;
}d[N];
int n,rk[N],sa[N];
string s;
inline bool cmp(Node a,Node b){
if(a.key1<b.key1)return 1;
if(a.key1>b.key1)return 0;
if(a.key2<b.key2)return 1;
if(a.key2>b.key2)return 0;
return a.i<b.i;
}
void SA(){
For(i,1,n)rk[i]=s[i]-'0'+1;//預處理長度為1的子串
for(int l=1;(1<<l)<n;l++){//倍增
int len=1<<(l-1);//已處理的長度
For(i,1,n){//處理第一第二關鍵字以及它所在的尾碼位置
d[i].key1=rk[i];
d[i].i=i;
if(i+len<=n)//如果有第二關鍵字就記錄
d[i].key2=rk[i+len];
else d[i].key2=0;//沒有就將優先順序變為最高
}
sort(d+1,d+1+n,cmp);//快排
int rank=1;
rk[d[1].i]=rank;
For(i,2,n){//合併第一第二關鍵字
if(d[i].key1==d[i-1].key1&&d[i].key2==d[i-1].key2)
rk[d[i].i]=rank;
else rk[d[i].i]=++rank;
}
if(rank==n)break;//如果排名已經都不相同了就退出迴圈
}
For(i,1,n)sa[rk[i]]=i;
}
signed main(){
cin>>s;
s=' '+s;
n=s.size()-1;
SA();
For(i,1,n)printf("%lld ",sa[i]);
return 0;
}
基數排序
可以直接把上面快排的部分直接換成基數排序。
Code
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5;
int sa[maxn], rank[maxn], newRank[maxn], sum[maxn], key2[maxn];
int n, m;
char str[maxn];
bool cmp(int a, int b, int l){
if(rank[a] != rank[b]) return false;
if( (a+l > n and b+l <= n) or (a+l <= n and b+l > n) ) return false;
if(a+l > n and b+l > n) return true;
return rank[a+l] == rank[b+l];
}
int main(){
scanf("%s", str+1);
n = strlen(str+1);
for(int i=1; i<=n; i++) sum[rank[i] = str[i]]++;
m = max(n, 256);
for(int i=1; i<=m; i++) sum[i]+=sum[i-1];
for(int i=n; i>=1; i--) sa[sum[rank[i]]--] = i;
for(int l=1; l<n; l<<=1){
int k = 0;
for(int i=n-l+1; i<=n; i++) key2[++k] = i;
for(int i=1; i<=n; i++) if(sa[i] > l) key2[++k] = sa[i]-l;
for(int i=1; i<=m; i++) sum[i] = 0;
for(int i=1; i<=n; i++) sum[rank[i]]++;
for(int i=1; i<=m; i++) sum[i]+=sum[i-1];
for(int i=n; i>=1; i--){
int j = key2[i];
sa[sum[rank[j]]--] = j;
}
int rk = 1;
newRank[sa[1]] = rk;
for(int i=2; i<=n; i++){
if(cmp(sa[i-1], sa[i], l)) newRank[sa[i]] = rk;
else newRank[sa[i]] = ++rk;
}
for(int i=1; i<=n; i++) rank[i] = newRank[i];
if(rk == n) break;
}
for(int i=1; i<=n; i++) printf("%d ",sa[i]);
return 0;
}



