摘要:常用於消除雜訊的圖像平滑方法包括三種線性濾波(均值濾波、方框濾波、高斯濾波)和兩種非線性濾波(中值濾波、雙邊濾波),本文將詳細講解三種線性濾波方法。 本文分享自華為雲社區《[Python從零到壹] 五十五.圖像增強及運算篇之圖像平滑(均值濾波、方框濾波、高斯濾波)》,作者:eastmount。 ...
摘要:常用於消除雜訊的圖像平滑方法包括三種線性濾波(均值濾波、方框濾波、高斯濾波)和兩種非線性濾波(中值濾波、雙邊濾波),本文將詳細講解三種線性濾波方法。
本文分享自華為雲社區《[Python從零到壹] 五十五.圖像增強及運算篇之圖像平滑(均值濾波、方框濾波、高斯濾波)》,作者:eastmount。
常用於消除雜訊的圖像平滑方法包括三種線性濾波(均值濾波、方框濾波、高斯濾波)和兩種非線性濾波(中值濾波、雙邊濾波),本文將詳細講解三種線性濾波方法。
一.圖像平滑
圖像平滑是一項簡單且使用頻率很高的圖像處理方法,可以用來壓制、弱化或消除圖像中的細節、突變、邊緣和雜訊,最常見的是用來減少圖像上的雜訊[1]。何為圖像雜訊?雜訊是妨礙人的感覺器官所接受信源信息理解的因素,是不可預測只能用概率統計方法認識的隨機誤差。從圖1中,可以觀察到雜訊的特點:位置隨機、大小不規則,將這種雜訊稱為隨機雜訊,這是一種常見的雜訊類型。

圖2是一個圖像平滑的示例,圖中左半部分是包含雜訊的原始輸入圖像,右半部分是進行圖像平滑後的圖像。通過對比容易觀察到,在平滑後的圖像中,物體中的雜訊得到了有效地抑制和消除,但花的邊緣部分被進行了模糊,這種將圖像中的冗餘信息進行抑制,即花的雜訊進行消除的過程被稱為圖像平滑[2]。

一幅圖像不可避免地要受到各種雜訊源的干擾,所以雜訊濾除往往是圖像處理中的第一步,濾波效果好壞將直接影響後續處理結果,雜訊濾除在圖像處理中占有相當重要的地位。雜訊濾除演算法多種多樣,可以從設計方法上分為線性濾波演算法和非線性濾波演算法兩大類。
(1)線性濾波
在圖像處理中,對鄰域中的像素的計算為線性運算時,如利用視窗函數進行平滑加權求和的運算,或者某種捲積運算,都可以稱為線性濾波。在數字信號處理和數字圖像處理的早期研究中,線性濾波器是雜訊抑制處理的主要手段,如均值濾波、方框濾波、高斯濾波等。
線性濾波演算法對高斯型雜訊有較好的濾波效果,而當信號頻譜與雜訊頻譜混疊時或者當信號中含有非疊加性雜訊時(例如由系統非線性引起的雜訊或存在非高斯雜訊等),線性濾波器的處理結果就很難令人滿意。
(2)非線性濾波
非線性濾波利用原始圖像跟模版之間的一種邏輯關係得到結果,如中值濾波、雙邊濾波等。非線性濾波技術從某種程度上彌補了線性濾波方法的不足,由於它能夠在濾除雜訊的同時較好地保持圖像信號的高頻細節,從而得到廣泛的應用。著名學者 Tukey [3]於1971年首次提出了一種非線性濾波器——中值濾波器,從此揭開了非線性濾波方法研究的序幕。非線性濾波技術發展到現在,基於中值濾波的改進演算法層出不窮,在非線性濾波演算法中占有重要的地位。另外很多新的非線性濾波演算法也相繼涌現,如基於數學形態學的濾波方法、基於模糊理論的濾波方法、基於神經網路的濾波方法等,它們為圖像濾波技術提供新的思路[4-5]。
後文將詳細介紹以下常用的一些濾波器,包括均值濾波、方框濾波、高斯呂波、中值濾波等,如表23-1所示。
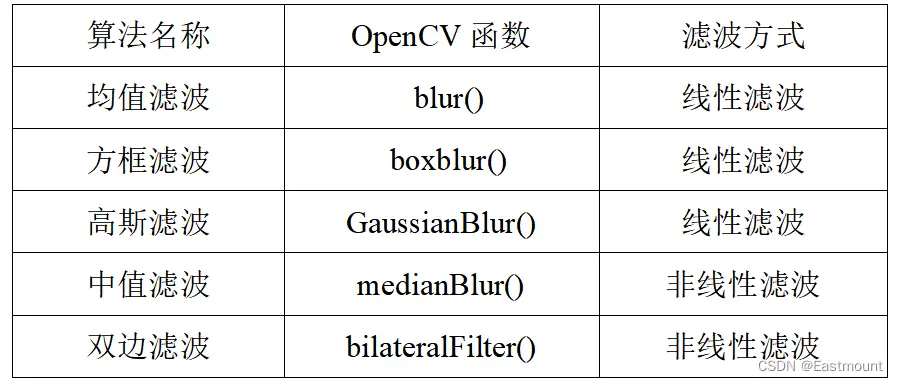
圖3為這五種濾波的效果對比,從濾波的結果可以看出各種濾波演算法對圖像的作用非常不同,有些變化非常大,有些甚至跟原圖一樣。在實際應用時,應根據雜訊的特點、期望的圖像和邊緣特征等來選擇合適的濾波器,這樣才能發揮圖像濾波的最大優點。

在圖像產生、傳輸和複製過程中,常常會因為多方面原因而被雜訊干擾或出現數據丟失,降低了圖像的質量。這就需要對圖像進行一定的增強處理以減小這些缺陷帶來的影響[6]。
二.均值濾波
均值濾波是最簡單的一種線性濾波演算法,它是指在原始圖像上對目標像素給一個模板,該模板包括了其周圍的臨近像素(以目標像素為中心的周圍8個像素,構成一個濾波模板,即去掉目標像素本身),再用模板中的全體像素的平均值來代替原來的像素值。換句話說,均值濾波輸出圖像的每一個像素值是其周圍M×M個像素值的加權平均值。
圖4表示均值濾波處理的過程,中心紅色點的像素值為藍色背景區域像素值求和的均值。5×5的矩陣稱之為模糊內核,針對原始圖像內的像素點,均值濾波採用核對其像素逐個進行均值處理,並得到最終的效果圖。
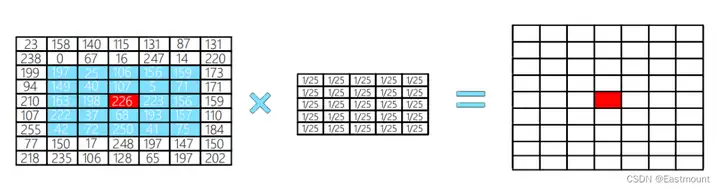
其中紅色區域的像素值均值濾波處理過程為:
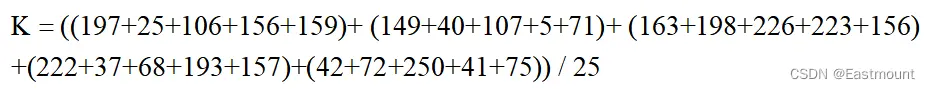
均值濾波演算法比較簡單,計算速度較快,對周期性的干擾雜訊有很好的抑製作用,但是它不能很好地保護圖像的細節,在圖像去噪的同時,也破壞了圖像的細節部分,從而使圖像變得模糊。
Python調用OpenCV中的cv2.blur()函數實現均值濾波處理,其函數原型如下所示,輸出的dst圖像與輸入圖像src具有相同的大小和類型。
dst = blur(src, ksize[, dst[, anchor[, borderType]]])
- src表示輸入圖像,它可以有任意數量的通道,但深度應為CV_8U、CV_16U、CV_16S、CV_32F或CV_64F
- ksize表示模糊內核大小,以(寬度,高度)的形式呈現
- anchor表示錨點,即被平滑的那個點,其預設值Point(-1,-1)表示位於內核的中央,可省略
- borderType表示邊框模式,用於推斷圖像外部像素的某種邊界模式,預設值為BORDER_DEFAULT,可省略
常見的模糊內核包括(3,3)和(5,5),如公式(2)和(3)所示:
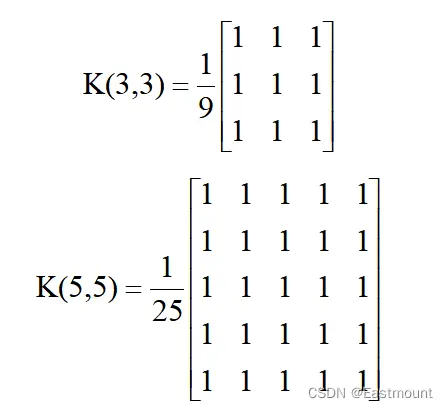
圖像均值濾波的Python實現代碼如下所示,需要註意的是,代碼中使用的是3×3的模板,plt.rcParams是用於設置中文漢字正常顯示。
# -*- coding: utf-8 -*- # By:Eastmount import cv2 import numpy as np import matplotlib.pyplot as plt #讀取圖片 img = cv2.imread('lena-zs.png') source = cv2.cvtColor(img,cv2.COLOR_BGR2RGB) #均值濾波 result = cv2.blur(source, (3,3)) #用來正常顯示中文標簽 plt.rcParams['font.sans-serif']=['SimHei'] #顯示圖形 titles = ['原始圖像', '均值濾波'] images = [source, result] for i in range(2): plt.subplot(1,2,i+1), plt.imshow(images[i], 'gray') plt.title(titles[i]) plt.xticks([]),plt.yticks([]) plt.show()
“lena”圖輸出結果如圖5所示,左邊表示含有雜訊的待處理原圖,右邊是均值濾波處理後的圖像,圖像中的椒鹽雜訊被去除了。

如果圖像中的雜訊仍然存在,可以增加模糊內核的大小,比如使用5×5、10×10,甚至20×20的模板。圖6就是使用10×10的內核,但是處理後的圖像會逐漸變得更模糊。

圖像均值濾波是通過模糊內核對圖像進行平滑處理,由於模糊內核中的每個權重值都相同,故稱為均值。該方法在一定程度上消除了原始圖像中的雜訊,降低了原始圖像的對比度,但也存在一定缺陷,它在降低雜訊的同時使圖像變得模糊,尤其是邊緣和細節處,而且模糊內核越大,模糊程度越嚴重。
三.方框濾波
圖像平滑利用捲積模板逐一處理圖像中每個像素,這一過程可以形象地比作對原始圖像的像素進行過濾整理,把鄰域像素逐一處理的演算法過程稱為濾波器。常見的線性濾波器包括均值濾波和方框濾波。
方框濾波又稱為盒式濾波,它利用捲積運算對圖像鄰域的像素值進行平均處理,從而實現消除圖像中的雜訊。方框濾波和和均值濾波的模糊內核基本一樣,區別為是否需要進行均一化處理。
Python調用OpenCV中的cv2.boxFilter()函數實現方框濾波處理,其函數原型如下所示:
dst = boxFilter(src, depth, ksize[, dst[, anchor[, normalize[, borderType]]]])
- src表示輸入圖像
- dst表示輸出圖像,其大小和類型與輸入圖像相同
- depth表示輸出圖像深度,通常設置為“-1”,表示與原圖深度一致
- ksize表示模糊內核大小,以(寬度,高度)的形式呈現
- normalize表示是否對目標圖像進行歸一化處理,預設值為true
- anchor表示錨點,即被平滑的那個點,其預設值Point(-1,-1)表示位於內核的中央,可省略
- borderType表示邊框模式,用於推斷圖像外部像素的某種邊界模式,預設值為BORDER_DEFAULT,可省略
常見的模糊內核ksize包括(3,3)和(5,5),如下所示:
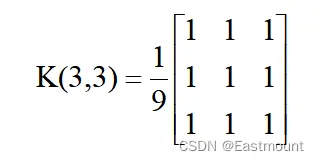
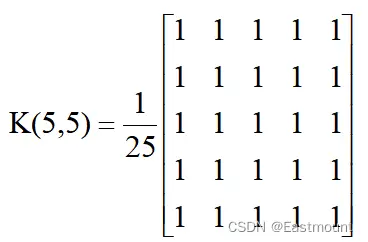
參數normalize表示是否對目標圖像進行歸一化處理。
- (1)當normalize為true時,需要執行歸一化處理,方框濾波就變成了均值濾波。其中,歸一化就是把要處理的像素值都縮放到一個範圍內,以便統一處理和直觀量化。
- (2)當normalize為false時,表示非歸一化的方框濾波,不進行均值化處理,實際上就是求周圍各像素的和。但此時很容易發生溢出,多個像素值相加後的像素值大於255,溢出後的像素值均設置為255,即白色。
參數normalize的定義如公式(6)所示。
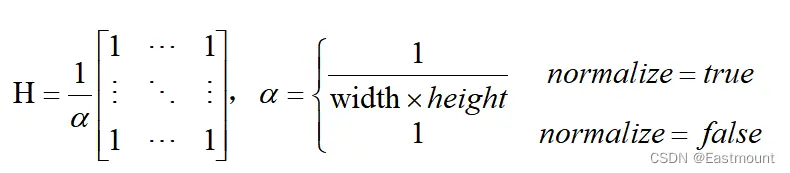
圖像方框濾波的Python實現代碼如下所示,代碼中使用3×3的核,normalize=0表示不進行圖像歸一化處理。
# -*- coding: utf-8 -*- # By:Eastmount import cv2 import numpy as np import matplotlib.pyplot as plt #讀取圖片 img = cv2.imread('lena-zs.png') source = cv2.cvtColor(img,cv2.COLOR_BGR2RGB) #方框濾波 result = cv2.boxFilter(source, -1, (3,3), normalize=0) #用來正常顯示中文標簽 plt.rcParams['font.sans-serif']=['SimHei'] #顯示圖形 titles = ['原始圖像', '方框濾波'] images = [source, result] for i in range(2): plt.subplot(1,2,i+1), plt.imshow(images[i], 'gray') plt.title(titles[i]) plt.xticks([]),plt.yticks([]) plt.show()
方框濾波非歸一化處理的輸出結果如圖7所示,處理後的效果圖中包含很多白色的像素點,這是因為圖像像素求和結果發生溢出(超過255)。由此可見,進行非歸一化的處理時,得到的圖像包含白色過多,對源圖像的毀壞太大。

如果設置2×2的模糊內核,其非歸一化的方框濾波處理效果更好一些,如圖23-8所示。核心代碼為:
- cv2.boxFilter(source, -1, (2,2), normalize=0)

下麵代碼是使用3×3內核,進行歸一化方框濾波處理的代碼,其輸出結果與3×3內核均值濾波完全相同。
# -*- coding: utf-8 -*- # By:Eastmount import cv2 import numpy as np import matplotlib.pyplot as plt #讀取圖片 img = cv2.imread('lena-zs.png') source = cv2.cvtColor(img,cv2.COLOR_BGR2RGB) #方框濾波 result = cv2.boxFilter(source, -1, (3,3), normalize=1) #用來正常顯示中文標簽 plt.rcParams['font.sans-serif']=['SimHei'] #顯示圖形 titles = ['原始圖像', '方框濾波'] images = [source, result] for i in range(2): plt.subplot(1,2,i+1), plt.imshow(images[i], 'gray') plt.title(titles[i]) plt.xticks([]),plt.yticks([]) plt.show()
輸出結果如圖9所示:

四.高斯濾波
為了剋服局部平均法造成圖像模糊的弊端,又提出了一些保持邊緣細節的局部平滑演算法,圖像高斯濾波(高斯平滑)就是這樣一種演算法。它是應用鄰域平均思想對圖像進行平滑的一種線性平滑濾波,對於抑制服從正態分佈的雜訊非常有效,適用於消除高斯雜訊,被廣泛應用於圖像處理的減噪過程。
圖像高斯濾波為圖像不同位置的像素值賦予了不同的權重,距離越近的點權重越大,距離越遠的點權重越小。它與方框濾波和均值濾波不同,它對鄰域內的像素進行平均時,為不同位置的像素賦予不同的權值。通俗地講,高斯濾波就是對整幅圖像進行加權平均的過程,每一個像素點的值,都由其本身和鄰域內的其他像素值(權重不同)經過加權平均後得到。
下麵是常用的3×3和5×5內核的高斯濾波模板。
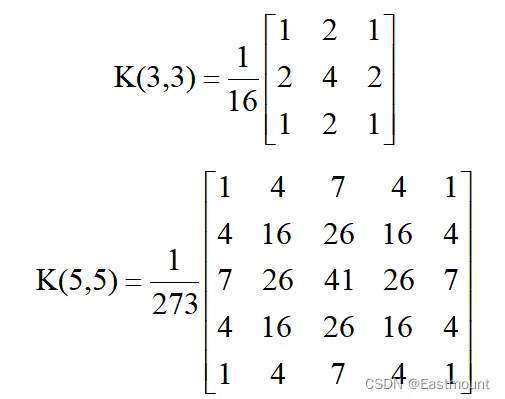
高斯濾波引入了數學中的高斯函數(正態分佈函數),一個二維高斯函數如下公式(9)所示,其中σ為標準差。高斯加權平均中,最重要是σ的選取,標準差代表數據離散程度,如果σ較小,則高斯分佈中心區域將更加聚集,平滑效果更差;反之,如果σ較大,高斯分佈中心區域將更離散,平滑效果更明顯[10]。
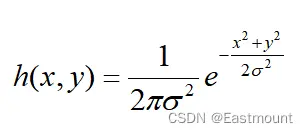
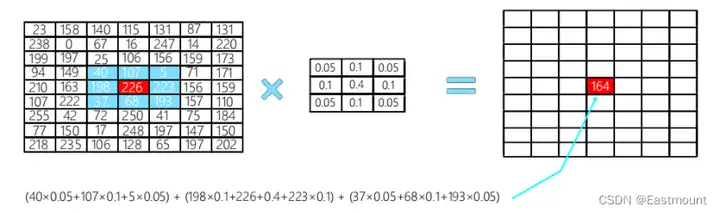
高斯濾波的核心思想是對高斯函數進行離散化,以離散點上的高斯函數值為權值,對圖像中的每個像素點做一定範圍鄰域內的加權平均,從而有效地消除高斯雜訊。高斯濾波讓臨近中心的像素點具有更高的重要度,對周圍像素計算加權平均值,如圖10所示,其中心位置權重最高為0.4。
Python中OpenCV主要調用GaussianBlur()函數實現高斯平滑處理,函數原型如下所示:
dst = GaussianBlur(src, ksize, sigmaX[, dst[, sigmaY[, borderType]]])
- src表示待處理的輸入圖像
- dst表示輸出圖像,其大小和類型與輸入圖像相同
- ksize表示高斯濾波器模板大小,ksize.width和ksize.height可以不同,但它們都必須是正數和奇數,它們也可以是零,即(0, 0)
- sigmaX表示高斯核函數在X方向的高斯內核標準差
- sigmaY表示高斯核函數在Y方向的高斯內核標準差。如果sigmaY為零,則設置為等於sigmaX,如果兩個sigma均為零,則分別從ksize.width和ksize.height計算得到
- borderType表示邊框模式,用於推斷圖像外部像素的某種邊界模式,預設值為BORDER_DEFAULT,可省略
下麵代碼是使用7×7核模板進行高斯濾波處理。
# -*- coding: utf-8 -*- # By:Eastmount import cv2 import numpy as np import matplotlib.pyplot as plt #讀取圖片 img = cv2.imread('lena-zs.png') source = cv2.cvtColor(img,cv2.COLOR_BGR2RGB) #高斯濾波 result = cv2.GaussianBlur(source, (7,7), 0) #用來正常顯示中文標簽 plt.rcParams['font.sans-serif']=['SimHei'] #顯示圖形 titles = ['原始圖像', '高斯濾波'] images = [source, result] for i in range(2): plt.subplot(1,2,i+1), plt.imshow(images[i], 'gray') plt.title(titles[i]) plt.xticks([]),plt.yticks([]) plt.show()
輸出結果如圖11所示,左邊為待處理圖像,右邊為高斯濾波處理後圖像。

圖12是使用15×15高斯核模板進行高斯濾波處理的效果圖,由圖可知,圖像在去除雜訊的同時也變得更加模糊。

總之,高斯濾波作為最有效的濾波器之一,它對於抑制服從正態分佈的雜訊非常有效。
五.總結
本文主要講解了常用於消除雜訊的圖像平滑方法,常見方法包括三種線性濾波(均值濾波、方框濾波、高斯濾波)和兩種非線性濾波(中值濾波、雙邊濾波)。這篇文章介紹了均值濾波、方框濾波和高斯濾波,通過原理和代碼進行對比,分別講述了各種濾波方法的優缺點,有效地消除了圖像的雜訊,並保留圖像的邊緣輪廓。
參考文獻:
- [1]岡薩雷斯著,阮秋琦譯. 數字圖像處理(第3版)[M]. 北京:電子工業出版社,2013.
- [2]zhu_hongji. [OpenCV學習筆記] 之圖像平滑(線性/非線性濾波器)[EB/OL]. (2018-08-11). https://blog.csdn.net/zhu_hongji/article/details/81479571.
- [3]陸瑤. 圖像處理與matlab實例之圖像平滑(一)[EB/OL]. (2017-07-23). https://www.cnblogs.com/luyaoblog/p/7160948.html.
- [4]阮秋琦. 數字圖像處理學(第3版)[M]. 北京:電子工業出版社,2008.
- [5]石振剛. 基於模糊邏輯的圖像處理演算法研究[D]. 東北大學, 2009.
- [6]馬光豪. 基於稀疏高頻梯度和聯合雙邊濾波的圖像平滑演算法研究[D].山東大學, 2018.
- [7]陳初俠. 圖像濾波及邊緣檢測與增強技術研究[D].合肥工業大學, 2009.
- [8]毛星雲,冷雪飛. OpenCV3編程入門[M]. 北京:電子工業出版社,2015.
- [9]Eastmount. [Python圖像處理] 四.圖像平滑之均值濾波、方框濾波、高斯濾波及中值濾波[EB/OL]. (2018-09-02). https://blog.csdn.net/Eastmount/article/details/82216380.
- [10]Eastmount. [數字圖像處理] 七.MFC圖像增強之圖像普通平滑、高斯平滑、Laplacian、Sobel、Prewitt銳化詳解[EB/OL]. (2015-06-08). https://blog.csdn.net/eastmount/article/ details/46378783.



