P6818 [PA2013]Działka

前言

我太菜了。。。。

對著 jiangly 大佬的題解研究了一下午研究了一下午才搞出來（淚目。

作為一個蒟蒻，我就詳細的講一下我對與本題的理解。

題意

本題的的題意描述的還是比較明瞭。

在二維坐標系中，輸入 \(n\) 個點 \(m\) 次詢問，

每次詢問，給出一個矩陣，

求出矩陣內極大凸包的面積。

題解

1.如何求面積

二維平面的計算幾何題，較常見的做法就是利用叉積。本題亦如此。

叉積有個優美的性質，我們可以發現對於 \(\vec{a} \times \vec{b}\) 可以在二維平面賦予特殊意義（ \(S\) 為三角形面積）。

\(\vec{a} \times \vec{b} = 2S\)

利用這個性質我們就可以求出任意凸包的面積。

舉個例子，\(4\) 個點坐標為 \((1 , 1) (1 , 3) (3 , 3) (3 , 1)\) 在此記為 \(0\) 號點到 \(3\) 號點，\(G\) 記為原點，

那要求出其凸包的面積就可以寫作：

\({ \vec{G0} \times \vec{G3} + \vec{G3} \times \vec{G2} + \vec{G1} \times \vec{G0} + \vec{G1} \times \vec{G0} \over 2}\)

其實就可以理解為綠色的三角形相加。

再容斥一下減去紅色三角(由於叉乘的順尋原因出來的紅色三角形負數)。

剩下的就是索要求的凸包面積。

因為本題 \(n \le 3000\) 我們可以考慮直接 \(O(n ^ 2)\) 預處理出每兩個向量的叉乘(其實不是任意兩個的叉乘，詳見第三部分)。

呢麽下麵的任務就是快速找到凸包外面的點。

2.如何找凸包

如何找凸包呢？有一個十分優雅的方法。可以考慮尋找類似於四分之一扇形的凸包，然後每次旋轉找到 \(4\) 個半圓再求和。假設我們先找右上角的扇形。

對於如下圖形如何優美的找到凸包呢？

我們可以考慮將點以優先 \(x\) 從大到小後 \(y\) 從大到小的順序找（過程可以順便預處理前面提到的任意兩點的距離）。

手模一下發現，我們先會從 \(1\) 號點就可以輕易的找到 \({1 , 3 , 4}\) 的點集。

呢如何記錄高效的記錄答案呢？

3.如何記錄答案

直接枚舉每個問題，顯然會 T 飛。

考慮在記錄兩點間距離的時候直接記錄最外面凸包的距離，例如前面的圖片，在記錄 \(\vec{1} \times \vec{4}\) 的時可以直接記錄為 \(\vec{1} \times \vec{3} + \vec{3} \times \vec{4}\)。樣我們在統計答案的時候實際上只需要記錄只需要記錄他最接近邊界的兩個點就可了。

考慮每一次記錄答考慮使用線段樹加掃描線的思想，如下圖為每個點。

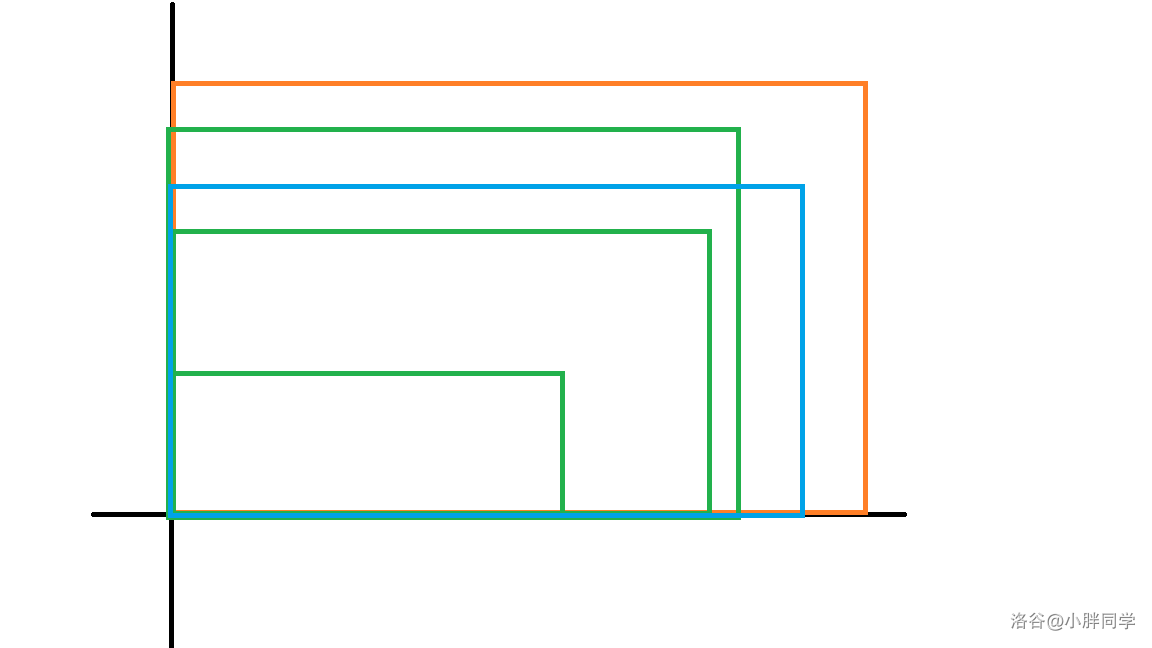
當我們更新完最外面的橙色的點還沒有處理藍色的點的時候，考慮有哪些區間里的提問是可以被更新的。

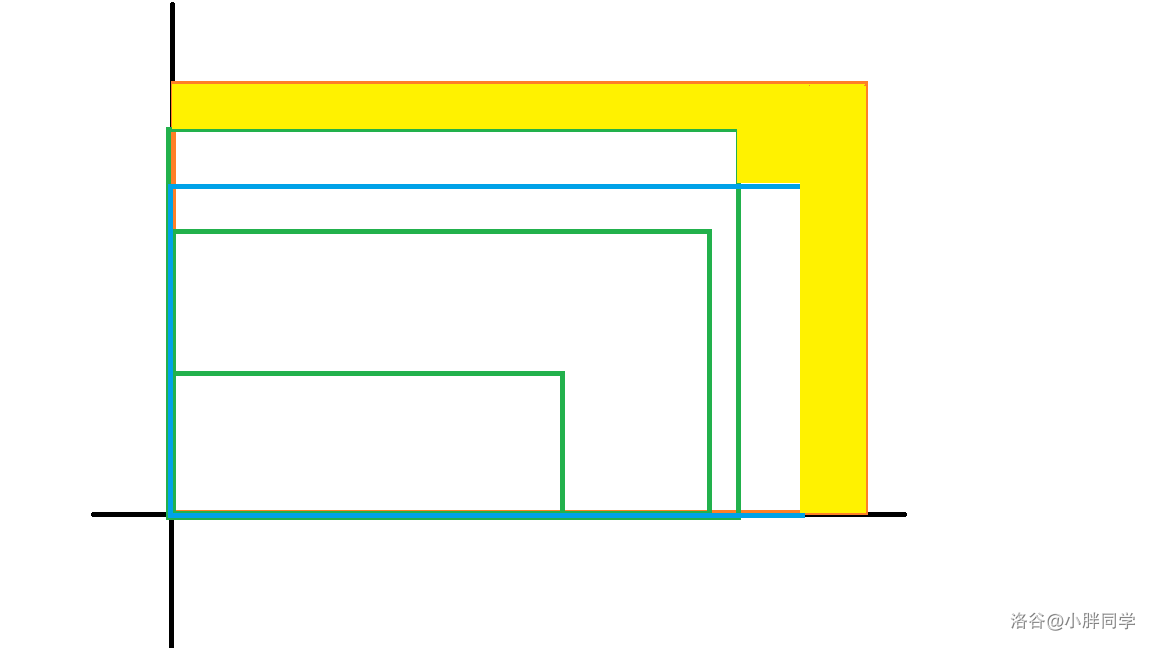
黃色的區間是可以被更新的，利用掃描線的思想做到 \(O(m \log m)\) 維護每個圖形的邊界。

\(\bullet\) 加強版

模擬賽出了這道題的加強版，若坐標的範圍改成 \(-10^7 \le x ,y \le 10^7\)。

兩個辦法，一是使用效率更高的 zkw 線段樹，二是數據離散化。

當然本題用普通線段樹就可以切了。

Code

代碼跟 jiangly 大佬的沒有本質區別，就不粘了（doge去翻上一篇題解吧。