題目一:在一個採用頁式虛擬存儲管理的系統中,有一用戶作業,它依次要訪問的頁面序列是1,2,3,4,1,2,5,1,2,3,4,5.假定分配給該作業的頁數為3且作業初始時未裝載頁面,那麼採用FIFO調度演算法產生的缺頁中斷數為多少,採用LRU調度演算法產生的缺頁中斷數為多少? 解析: FIFO調度演算法:先 ...
題目一:在一個採用頁式虛擬存儲管理的系統中,有一用戶作業,它依次要訪問的頁面序列是1,2,3,4,1,2,5,1,2,3,4,5.假定分配給該作業的頁數為3且作業初始時未裝載頁面,那麼採用FIFO調度演算法產生的缺頁中斷數為多少,採用LRU調度演算法產生的缺頁中斷數為多少?
解析:
FIFO調度演算法:先進先出原則,當記憶體中存在,則保持不變;不存在,則將右側調出,左側調入記憶體;
整體操作邏輯如下:
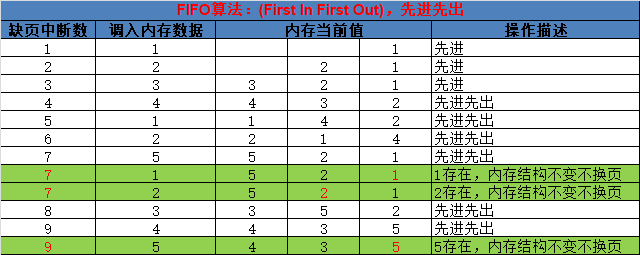
最核心的是綠色背景的這幾個操作,由於1,2,5存在,就不會產生缺頁中斷。
經上圖分析,FIFO演算法產生的缺頁中斷樹是9; 總訪問頁數是12,所以缺頁中斷率 = 缺頁中斷次數 / 總訪問頁數 = 9 / 12
而LRU調度演算法,採用的是最近最少使用演算法,當記憶體中存在,則把存在的調入到最前面,這樣做的好處是,對於使用比較頻繁的數據,無需重覆載入,能夠提高性能;
整體操作邏輯如下:
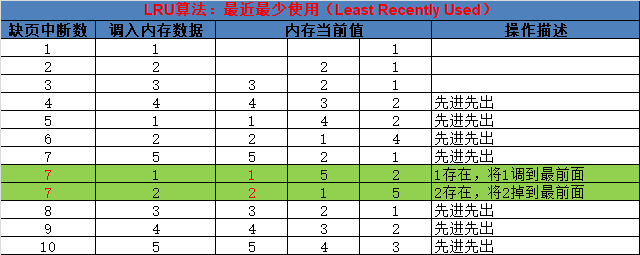
可以看到,綠色背景處,存在次序調換的操作,這種操作,能重新激活已存在的記憶體,讓其延遲調出。
經上圖分析,FIFO演算法產生的缺頁中斷樹是10; 總訪問頁數是12,所以缺頁中斷率 = 缺頁中斷次數 / 總訪問頁數 = 10 / 12
題目二:
某虛擬存儲系統採用最近最少使用(LRU)頁面淘汰演算法,假定系統為每個作業分配4個頁面的主存空間,其中一個頁面用來存放程式。現有某作業的
程式如下:
Var A: Array[1..100,1..100] OF integer;
i,j: integer;
FOR i:=1 to 100 DO
FOR j:=1 to 100 DO
A[i,j]:=0;
設每個頁面可存放200個整數變數,變數i、j存放在程式頁中。初始時,程式及i、j均已在記憶體,其餘3頁為空。若矩陣A按行序存放,那麼當程式執行完後共產
生( 1)次缺頁中斷;若矩陣A按列序存放,那麼當程式執行完後共產生( 2)次缺頁中斷。
1 A.50,B.100,C.5000,D.10000
2.A.50,B.100,C.5000,D.10000
解答:
此問題的前置條件是,每頁數據中行列的分佈情況,按照每行100條數據,總共兩行來分佈,可以存在的總數剛好是200個整數變數;
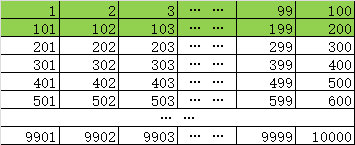
此問題考察的並非是最近最少,而是最簡單的缺頁中斷
如果按照行存儲的話,那麼很明顯每200條中斷一次,總共是10000/200=50次
如果按照列存儲的話,就變成如下情況了:
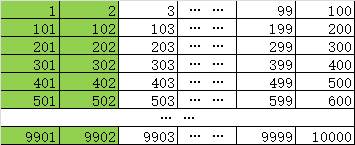
再看看程式里的訪問方式:
Array[0,0]、Array[0,1],Array[0,2]、Array[0,3],...Array[0,100]。每兩個數,就得中斷換頁一次,第一行就中斷50次,總共100行,供中斷50*100 = 5000次
所以答案是:1:A;2:C



