寫在開頭：本文章提供深搜與寬搜的解題思路，無具體題目對應的代碼，如想瞭解，請到個人主頁查找，感謝觀看。

深度優先搜索（DFS）：

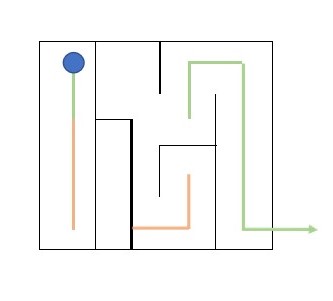
遞歸，即函數調用自身，以逐步減小問題 的規模。但在一些問題中，並不是所有的 遞歸路徑都是有效的。 如圖所示迷宮，很可能會進入橙色所標識 的“死衚衕”，只能回到之前的路徑，直到 找到綠色的解為止。

這種方法被稱為回溯法。 回溯法往往會嘗試一條儘可能深而完整的搜索路線，直至完全無 法繼續遞歸時才回溯，因而需要用深度優先搜索(DFS) 實現。

所以學會深度優先搜索前一定要深刻理解遞歸，先來看一段代碼：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 void dfs(int x){
 4     if(x==0) 
 5         return;
 6     cout<<x<<endl;
 7     dfs(x-1);
 8     cout<<"*"<<x<<endl;
 9 }
10 int main(){
11     dfs(5);
12     return 0;
13 } 

結果為：

5
4
3
2
1
*1
*2
*3
*4
*5

因為函數的不斷嵌套，cout<<"*"<<x<<endl;  始終不會運行，只有x-1=0時才會一層一層由小到大執行這一行。

下麵是回溯的一般形式：

 1 回溯演算法的一般形式如下:
 2 void dfs(int k) { // k代表遞歸層數,或者說要填第幾個空
 3     if(所有空已經填完了){
 4         判斷最優解/記錄答案;
 5         return;    
 6     }
 7     for (枚舉這個空能填的選項)
 8         if (這個選項是合法的){//查看這個情況有沒有被占位 
 9             記錄下這個空(保存現場);//有時還需占位，例如四階數獨中的行、列、塊記錄 
10             dfs(k+1);
11             取消這個空(恢復現場);//如果占位了還需要取消占位 
12         }
13 }

廣度優先搜索(BFS)：

深搜會儘快完成一個可行的解，再回溯嘗試其他的可能性。 當解相對稀疏，或問題很大時，深搜可能陷入過深、過窄的“陷阱”，這個時候就需要用到寬搜。

廣度優先搜索可以保證在求解最近、最短、最快等一類問題時， 搜索到的首個解就是最優解。

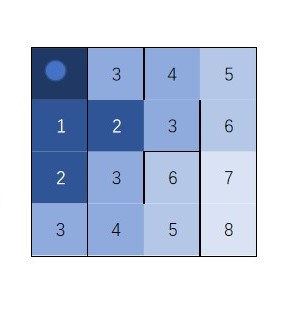
考慮另一種思路，從起點出發，類似於 潑水一般，讓水流順著多個方向同時蔓延。 這種方法被稱為洪泛法。 洪泛法會擴展相同層更多的可能性以拓寬廣 度，往往會使用廣度優先搜索(BFS) 實現。

先來瞭解一些關於隊列的函數（結果附在每行結束）：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 int main(){
 4     queue<int> a;
 5     cout<<a.empty()<<endl;//1
 6     a.push(10);//{10}
 7     cout<<a.front()<<endl;//{10}
 8     cout<<a.empty()<<endl;//0
 9     a.pop();//{}
10     cout<<a.empty()<<endl;//1    
11         
12     a.push(12);
13     a.push(13);
14     a.push(14);//{12,13,14}
15     cout<<a.front()<<endl;//{12}
16     
17     return 0;
18 } 

這樣再理解廣度優先搜索的演算法就簡單多了：

1 Q.push(初始狀態); // 將初始狀態入隊
2 while (!Q.empty()) {
3 State u = Q.front(); // 取出隊首
4 Q.pop();//出隊
5 for (枚舉所有可擴展狀態) // 找到u的所有可達狀態v
6 if (是合法的) // v需要滿足某些條件，如未訪問過、未在隊內等
7 Q.push(v); // 入隊(同時可能需要維護某些必要信息)
8 }

總結：

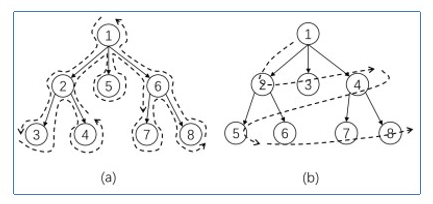
回溯法/深度優先搜索(上圖 a) ：

　　快速構造解，使用遞歸。不撞南牆心不死。 但進入死路就回頭了。

洪泛法/廣度優先搜索(上圖 b):

　　 尋找最優解，使用隊列 從起點開始，逐層往外擴展。

　　優化技巧（剪枝）：將不可能的解提前剪掉。