樹狀數組介紹 樹狀數組,顧名思義,就是樹狀的一維數組。 二叉樹同樣也可以用一維數組存儲。我們以二叉樹進行類比。 如圖所示,圖中節點的序號就是存在數組中的下標。 記父節點序號為 $p$,子節點序號為 $s$。 則有: $p$ $=$ $s$ $/$ $2$ (向下取整)。 左子節點 $s_{left} ...
樹狀數組介紹
樹狀數組,顧名思義,就是樹狀的一維數組。
二叉樹同樣也可以用一維數組存儲。我們以二叉樹進行類比。

如圖所示,圖中節點的序號就是存在數組中的下標。
記父節點序號為 \(p\),子節點序號為 \(s\)。
則有:
\(p\) \(=\) \(s\) \(/\) \(2\) (向下取整)。
左子節點 \(s_{left}\) \(=\) \(p\) \(* 2\) 。
右子節點 \(s_{right}\) \(=\) \(p\) \(*2+1\) 。
綜上可知,二叉樹能用一維數組存,是由於其父子節點間存在一定關係,以至於不需要用額外的變數來表示信息。
那類比到樹狀數組中,可以發現:

\(c\)數組即為樹狀數組。\(c_i\) 表示區間\(a\)\([i-lowbit(i),i]\) 的和。
同樣記父節點下標為 \(p\) ,子節點下標為 \(s\)。
則有:
\(p\) \(=\) \(s\) \(+\) \(lowbit(s)\)。
由這條公式亦可反推出:
\(s\) \(=\) \(p\) \(-\) \(2^i\)(\(0 \le i < p_{last}\))
這裡的 \(p_{last}\) 指的是 \(p\) 二進位表示下最後一位 \(1\) 所在的位數。
例如:\(6\) 的二進位數表示為 \(110\),則它的 \(p_{last}\) 為 \(1\)。(這裡的位數從右往左從\(0\)開始記)。
因為公式 \(1\) 由 \(s\) 加上自身 \(lowbit(s)\) 得到 \(p\) 其過程一定會產生進位。且 \(lowbit(s)\) 一定小於 \(lowbit(p)\) ,所以可以倒推得到子節點。
由於以上關係,樹狀數組不僅可以用一維數組存。而且還衍生出了一系列用途。
樹狀數組功能
單點增加
Q:給序列中的一個數 \(a[x]\) 加上 \(y\) 。此時如何維護樹狀數組?
A:將所有包含 \(a[x]\) 的節點加上 \(y\) 即可,也就是 \(c[x]\) 和它所有的祖先節點。
ps:初始化時亦可運用此操作。
點擊查看代碼
void add(int x,int y){
for (; x <= N;x += x&-x) c[x] += y;
return ;
}
動態維護首碼和
之所以說動態維護,因為用樹狀數組維護首碼和只需要 \(\log N\) 的時間複雜度。更為優秀。
Q:求 \(a\) 數組 \(a_i \sim a_x\) 的和。
A:將數 \(x\) 分成若幹個區間。
區間共同特點:若區間結尾為 \(R\),則區間長度就等於 \(lowbit(R)\),即 \(R\) 二進位分解下最小的整數次冪。
舉例:當 \(x\) = \(7\) 時

如圖所示。
區間劃分方式與樹狀數組相同。前面又提到“\(c\)數組即為樹狀數組。\(c_i\) 表示區間\(a\)\([i-lowbit(i),i]\) 的和。”
因此只需要將這幾個區間所對應的 \(c_i\) 相加。即可得到首碼和。
點擊查看代碼
int ask(int x){
int ans = 0;
for (; x ; x -= x & -x) ans += c[x];
return ans;
}
例題【具體應用】
主要利用樹狀數組可以快速求首碼和的優勢,以數據範圍為下標,快速統計區間內的個數(或所需要的信息),適用於數據範圍適中(一般為 \(0 \le x \le 10^6\))且需要多次求首碼和的題目。
【例題1】 三元上升子序列
【題目分析】
對於一個數 \(x\) ,計算其作為 \(j\) 時,位置在它前面比它小的數 \(x_{min}\)、位置在它後面比它大的數 \(x_{max}\),運用乘法原理的知識可知,將\(x_{min} \times x_{max}\),即可得到 \(x\) 作為 \(j\) 時的方案數 ,枚舉所有 \(x\) ,即可得到總方案數。
【樹狀數組作用】
統計 \(x_{min}\) 和 \(x_{max}\) 時,即可將數 \(x\) 的範圍作為樹狀數組的下標。
此時兩種操作所代表的意思分別為:
\(add(x,1)\) 表示數值為 \(x\) 的數的個數 \(+1\)。
\(sum(y)\) 表示在已經掃描過的區間內,數值為從 \(1 \sim y\) 的所有數的個數。
順序掃描序列,對於數 \(x\) ,統計兩個信息。
\(r_{i,0}\) 表示位置在數 \(x\) 前面,且比它小的數。
\(r_{i,1}\) 表示位置在數 \(x\) 前面,且比它大的數。
位置在數 \(x\) 後面,且比數 \(x\) 大的數就等於:
\(所有數 - 所有位置在 x 前面比 x 小的數 - r{i,1}\)。
【code】
點擊查看代碼
#include<iostream>
#include<cstdio>
#include<cmath>
#define ll long long
using namespace std;
ll tree[100005],n,num;
ll r[40005][2],a[100005];
void add(ll x,ll y){
for(;x<=100005;x+=(x&-x)) tree[x]+=y;
}
ll sum(ll x){
ll ans=0;
for(;x;x-=(x&-x)) ans+=tree[x];
return ans;
}
int main(){
scanf("%lld",&n);
for(int i=1;i<=n;i++){
ll x;
scanf("%lld",&x);
a[i]=x;
num=max(num,x);
add(x,1);
r[i][0]=sum(x-1);
r[i][1]=sum(num)-sum(x);
}
ll ans=0;
for(int i=1;i<=n;i++)
ans+=r[i][0]*(sum(num)-sum(a[i])-r[i][1]);
cout<<ans<<endl;
return 0;
}
【summary】
此題算是初步認識了以數值範圍為下標的樹狀數組的用法。下一大點求逆序對的思想與此相同。
【例題2】 [USACO04OPEN] MooFest G 加強版
【題目分析】
將奶牛按照音量從小到大進行排序,保證當前奶牛的音量一定最大,然後分類討論所有比當前奶牛音量小的奶牛與當前奶牛的距離(坐標比當前奶牛大的和坐標比當前奶牛小的)。兩者相加,乘上當前奶牛音量,枚舉每個奶牛,即可得到答案。
【樹狀數組作用】
定義兩個樹狀數組,都是以距離的範圍作為下標, \(c\) 數組用於統計對應距離的個數,\(t\) 數組用於表示對應距離 \(\times\) 對應 距離個數的總數,通過二者,即可快速計算距離差。
【code】
計算過程的解釋已在代碼中註釋出來。
點擊查看代碼
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define ll long long
using namespace std;
ll n,t[50005],c[50005];
struct A{
ll v,x;
}a[50005];
bool cmp(A xx,A yy){
if(xx.v==yy.v) return xx.x<yy.x;
return xx.v<yy.v;
}
void addc(ll x,ll y){
for(;x<=50000;x+=(x&-x)) c[x]+=y;
}
void addt(ll x,ll y){
for(;x<=50000;x+=(x&-x)) t[x]+=y;
}
ll sumc(ll x){
ll sum=0;
for(;x;x-=(x&-x)) sum+=c[x];
return sum;
}
ll sumt(ll x){
ll sum=0;
for(;x;x-=(x&-x)) sum+=t[x];
return sum;
}
int main(){
scanf("%lld",&n);
for(int i=1;i<=n;i++) scanf("%lld%lld",&a[i].v,&a[i].x);
sort(a+1,a+n+1,cmp);
ll ans=0,max_num=0;
for(int i=1;i<=n;i++){
max_num=max(max_num,a[i].x);
//以下距離之間的比較限於所有音量比當前奶牛小的奶牛。
//a[i].x*sumc(a[i].x-1) 表示當前奶牛的距離*距離比當前奶牛小的奶牛個數。
//sumt(a[i].x-1) 表示所有距離比當前奶牛小的奶牛的距離和。
//sumt(max_num)-sumt(a[i].x) 表示所有距離比當前奶牛大的奶牛的距離之和。
//sumc(max_num)-sumc(a[i].x))*a[i].x 表示當前奶牛距離 * 距離比當前奶牛大的奶牛個數
ans+=a[i].v*(a[i].x*sumc(a[i].x-1)-sumt(a[i].x-1)+(sumt(max_num)-sumt(a[i].x))-(sumc(max_num)-sumc(a[i].x))*a[i].x) ;
addc(a[i].x,1);
addt(a[i].x,a[i].x);
}
cout<<ans<<endl;
return 0;
}
【summary】
這一題的重點給到題目中樹狀數組 \(t\)。主要收穫為:以數值範圍為下標的樹狀數組,能夠處理的信息不僅限於個數。
【例題3】P1972 [SDOI2009] HH的項鏈
【題意分析】
本題核心:如何判斷一個區間內的貝殼是否重覆?
當右端點 \(r\) 固定時,不論 \(l\) 取何值,對於任意一組重覆的貝殼,都可以只統計最右端的貝殼。
原因:設一組重覆貝殼中最右端的貝殼所在的位置為 \(pos_r\),那麼當 \(pos_r < l\) 時,其他貝殼也不可能算進統計中,當 $pos_r \ge l $時,無論其他貝殼是否被包括,對於區間的貢獻都只有 \(1\),因此,只計算最右端的貝殼即可。
因此,只需要將所有詢問區間按 \(r\) 從小到大排序,計算答案即可。
【樹狀數組作用】
以位置為下標,每遇到一個新的數 \(num(num \le r)\),判斷它是否重覆,如果重覆,那麼將上一個相同的數的貢獻值 \(-1\),將當前數的貢獻值 \(+1\)。
對於一段區間 \([l,r]\),答案為 \(sum(r)-sum(l-1)\)。
【code】
點擊查看代碼
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
int n,m,ask_r,prev,pos;
int vis[1000005],a[1000005],t[1000005],ans[1000005];
struct A{
int l,r,num;
}ask[1000005];
bool cmp(A x,A y){
return x.r<y.r;
}
int find(int pos){
ask_r=ask[pos++].r;
while(ask_r==ask[pos].r) pos++;
return pos-1;
}
void add(int x,int y){
for(;x<=n;x+=(x&-x)) t[x]+=y;
return;
}
int sum(int x){
int su=0;
for(;x;x-=(x&-x)) su+=t[x];
return su;
}
void replace(){
for(int i=ask[prev].r+1;i<=ask_r;i++){
if(vis[a[i]]!=0) add(vis[a[i]],-1);
add(i,1);
vis[a[i]]=i;
}
for(int i=prev+1;i<=pos;i++) ans[ask[i].num]=sum(ask[i].r)-sum(ask[i].l-1);
return;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
scanf("%d",&m);
for(int i=1;i<=m;i++) scanf("%d%d",&ask[i].l,&ask[i].r),ask[i].num=i;
sort(ask+1,ask+m+1,cmp);
while(1){
if(pos==m) break;
prev=pos;
pos=find(pos+1);
replace();
}
for(int i=1;i<=m;i++) cout<<ans[i]<<endl;
return 0;
}
【\(summary\)】
此題不再以數據範圍為下標,而是以位置為下標。對於樹狀數組的應用更加靈活。在想到以最右端的貝殼為有價值的貢獻時,對應到樹狀數組的操作就可以是上一個重覆的數的貢獻值 \(-1\),當前數的貢獻值 \(+1\)。然後用首碼和統計區間內的個數。算進一步的開闊思維。
求逆序對
本質上也是通過樹狀數組單點增加和區間求和的操作進行計算。作為一個專題單獨列出來。
桶排+樹狀數組:
1.桶排部分:
對於一個序列 \(a\) , 我們建立一個 \(cnt\) 數組,\(cnt[x]\) 表示 \(x\) 在序列 \(a\) 中出現過的次數。當 \(a_i=val\) 時,\(cnt[val]++\)。
2.樹狀數組部分:
倒序掃描序列 \(a\),對於新加入的數 \(a_i\),查詢 \(cnt[1~a_i-1]\) 的首碼和,並將返回的首碼和加入答案。首碼和部分就可以用樹狀數組來維護。
操作簡單粗暴,但相當好用。
點擊查看代碼
for ( int i = n; i; i --) {
ans += ask (a[i] - 1);
add (a[i] , 1 );
}
【例題】
接下來通過兩道題進一步瞭解一下逆序對的考法。(不做一下真沒想到還能這樣考。)
【例題1】P2448 無盡的生命
【題意簡述】
看到題目顯而易見是求逆序對個數。
【思路分析】
看到數據範圍 \(x_i,y_i \le 2^{31}-1\),\(k \le 10^5\)。數據值域大但是個數少,且與數據之間的大小關係有關,因此考慮離散化。
離散化簡單介紹
離散化實際就是一種映射,當數據值域過大而個數有限時,可以嘗試離散化。
具體過程以此題為例。假設給出這麼一組數據
2
123456789 123456
987654321 123456
首先將所有出現過的數收集起來,存進 \(a\) 數組,併進行排序,然後再去重保存進 \(pos\) 數組當中。

接下來就可以建立映射關係。將數值大的數在 \(num\) 數組中用數值小的數代替,但各個數之間的大小關係不變,接下來交換操作先用二分答案在 \(pos\) 數組中檢索,然後通過映射在 \(num\) 數組中進行交換。
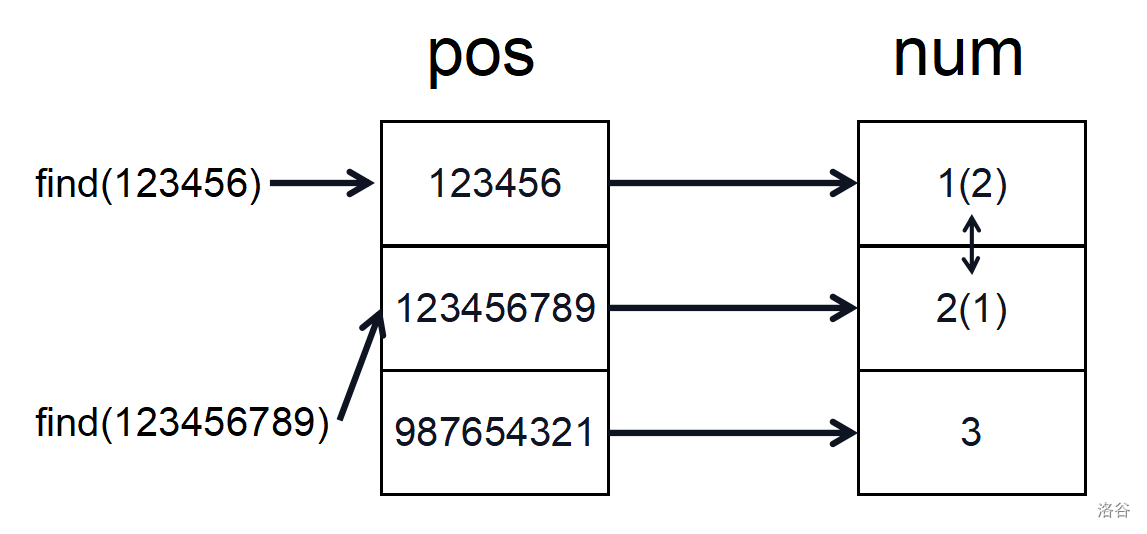
最終被交換過的數之間的逆序對在 \(num\) 數組中求即可。
被交換的數與未被交換的數之間的逆序對
考慮每個被交換的數對答案的貢獻。
設 \(x<y\),當 \(x\) 和 \(y\) 交換後。
對於 \(x\) 來說, \(x \sim y\) 之間所有未被交換的數都比 \(x\) 大,形成逆序對。
對於 \(y\) 來說,\(x \sim y\) 之間所有未被交換的數都比 \(y\) 小,形成逆序對。
逆序對個數都為\(x \sim y\) 之間所有未被交換的數。
溫馨提示:以下主要為代碼實現講解,本質思想同上。
對於交換過後的 \(num\) 數組,\(num_i\) 表示的是位置 \(pos_i\) 上當前所在的數在 \(num\) 數組中對應的數。記數 \(x\) 為位置 \(pos_i\) 上當前所在的數。
\(pos_{num_i}\) 表示數 \(x\) 現在所在的位置。
\(pos_i\) 表示數 \(x\) 原來在的位置。
\(\left\vert pos_i-pos_{num_i}-1\right\vert\) 表示兩個位置間所有的數。
\(\left\vert num_i-i-1\right\vert\) 表示兩個位置間所有被交換過的數。
因此所有未被交換的數就為 \(\left\vert pos_i-pos_{num_i}-1\right\vert - \left\vert num_i-i-1\right\vert\)。
【code】
點擊查看代碼
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
struct A{
int x,y;
}a[100005];
int k,pos[200005],num[200005],cnt,len;
int t[100005];
void add(int x){
for(;x<=len;x+=(x&-x)) t[x]+=1;
}
long long sum(int x){
long long ans=0;
for(;x;x-=(x&-x)) ans+=t[x];
return ans;
}
int find(int x){
int l=1,r=len;
while(l<r){
int mid=(l+r)>>1;
if(pos[mid]<x) l=mid+1;
else if(pos[mid]>x) r=mid-1;
else return mid;
}
}
int main(){
scanf("%d",&k);
for(int i=1;i<=k;i++){
scanf("%d%d",&a[i].x,&a[i].y);
num[++cnt]=a[i].x;
num[++cnt]=a[i].y;
}
sort(num+1,num+cnt+1);
for(int i=1;i<=cnt;i++){
if(num[i]==num[i-1]) continue;
pos[++len]=num[i];
}
for(int i=1;i<=len;i++) num[i]=i;
for(int i=1;i<=k;i++){
int pos1=find(a[i].x);
int pos2=find(a[i].y);
swap(num[pos1],num[pos2]);
}
long long ans=0;
for(int i=len;i>=1;i--){
add(num[i]);
ans+=sum(num[i]-1);
ans+=abs(pos[num[i]]-pos[i]-1)-abs(num[i]-i-1);
}
cout<<ans<<endl;
return 0;
}
【summary】
重點在於與未交換的數之間的求解。題目中序列的長度可以長到一個數組都存不下,但卻可以用公式求呢。
【例題2】P3531 [POI2012]LIT-Letters
【題目描述】
該題的重點在於如何從題面描述轉到求 \(逆序對\)。抓到重點:
-
交換 \(a\) 中相鄰兩個字元,求最少的交換次數。
-
\(a,b\) 中只含大寫字母,且數據保證 \(a\) 可以變成 \(b\)。
對 \(b\) 串中的字元進行順序編號(假設此時 \(b\) 中並沒有重覆的字母),並對應到 \(a\) 串中。
例如:
3
ABC
BCA
對 \(BCA\) 進行順序編號,對應到 \(ABC\) 就是 \(312\)。
當序列 \(a\) 中存在數 \(a , b\),滿足 $pos_a < pos_b $ , \(a > b\)。也就是形成逆序對。
而對於我們的目標,將 \(a\) 串變成 \(b\) 串,需滿足任意數 \(a , b\),都有 \(pos_a < pos_b\) , \(a < b\)。
顯然我們需要通過一定操作,令逆序對都消失,以達到目標。
由於題目中的交換為交換相鄰的數,因此只要 \(a\) 與 \(b\) 不交換,它們之間的相對位置就不會變,也就不能達成目標。
綜上所述,最少的交換次數就是逆序對的個數。
當字母重覆時,我們要如何讓編號對應到 \(a\) 呢?
顯然逆序對個數越少越好,因此對於相同的字母,按出現的順序進行順序編號。代碼中用單向鏈表實現。
【code】
點擊查看代碼
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#define ll long long
using namespace std;
int now[30],prev[30],nex[1000005];
char s[1000005],ss[1000005];
int a[1000005],t[1000005],lens;
void add(int x,int y){
for(;x<=lens;x+=(x&-x)) t[x]+=y;
return;
}
ll sum(int x){
ll ans=0;
for(;x;x-=(x&-x)) ans+=t[x];
return ans;
}
int main(){
scanf("%d",&lens);
cin>>(s+1);
cin>>(ss+1);
for(int i=1;i<=lens;i++){
int ch=s[i]-'A';
if(now[ch]==0) now[ch]=i;
nex[prev[ch]]=i;
prev[ch]=i;
}
for(int i=1;i<=lens;i++){
int ch=ss[i]-'A';
a[now[ch]]=i;
now[ch]=nex[now[ch]];
}
ll ans=0;
for(int i=lens;i>=1;i--){
add(a[i],1);
ans+=sum(a[i]-1);
}
cout<<ans<<endl;
return 0;
}
區間增加,單點查詢
思路剖析
相信經過上面的頭腦風暴,再來看這題已經相當簡單了。
此時主要運用到差分的思想,差分是首碼和的逆運算。
當要在區間 \([x,y]\) 加上 \(k\) 時,我們進行以下操作:
\(add(x,k) , add(y+1,-k)\)
此時對於區間求首碼和對於 \(x \sim y\),它的首碼和都為 \(k\),而到 \(y+1\) ,又變成 \(0\)。此時的首碼和正好是區間增加的數,且不會對其它數產生影響。
因此,當查詢第 \(x\) 個數時,只需要輸出:
\(a_x(第 x 個數原本的數值) + sum(x)(變化的值)\)。
即可。
code
點擊查看代碼
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int a[500005],c[500005],n,m;
void add(int x,int k){
for(;x<=n;x+=x&-x) c[x]+=k;
return;
}
int q(int x){
int sum=0;
for(;x;x-=x&-x) sum+=c[x];
return sum;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=m;i++){
int type;
scanf("%d",&type);
if(type==1){
int x,y,k;
scanf("%d%d%d",&x,&y,&k);
add(x,k);
add(y+1,-k);
}
else{
int x;
scanf("%d",&x);
cout<<a[x]+q(x)<<endl;
}
}
return 0;
}



