題目鏈接
可以通過參考一道例題來加深對dfs的認知和學習

題意描述

按照字典序輸出自然數 1 到 n 所有不重覆的排列，即 n 的全排列，要求所產生的任一數

字序列中不允許出現重覆的數字。

輸出格式

由 1 ∼ n 組成的所有不重覆的數字序列，每行一個序列。每個數字保留 5 個場寬。

• 數據範圍 ：1<= n <= 9

題目分析

輸入 ：

1

輸出 ：

    1    2    3
    1    3    2
    2    1    3
    2    3    1
    3    1    2
    3    2    1

觀察輸出樣例可知，5個場寬輸出的意思是每個數輸出時占5個位置且右對齊，就是以

" %5d "格式輸出

接著分析題目，求全排列，其實可以深搜，也就是dfs。

解題思路

演算法分析

我們以 n = 3 為例，可以構造一顆搜索樹來進行搜索。

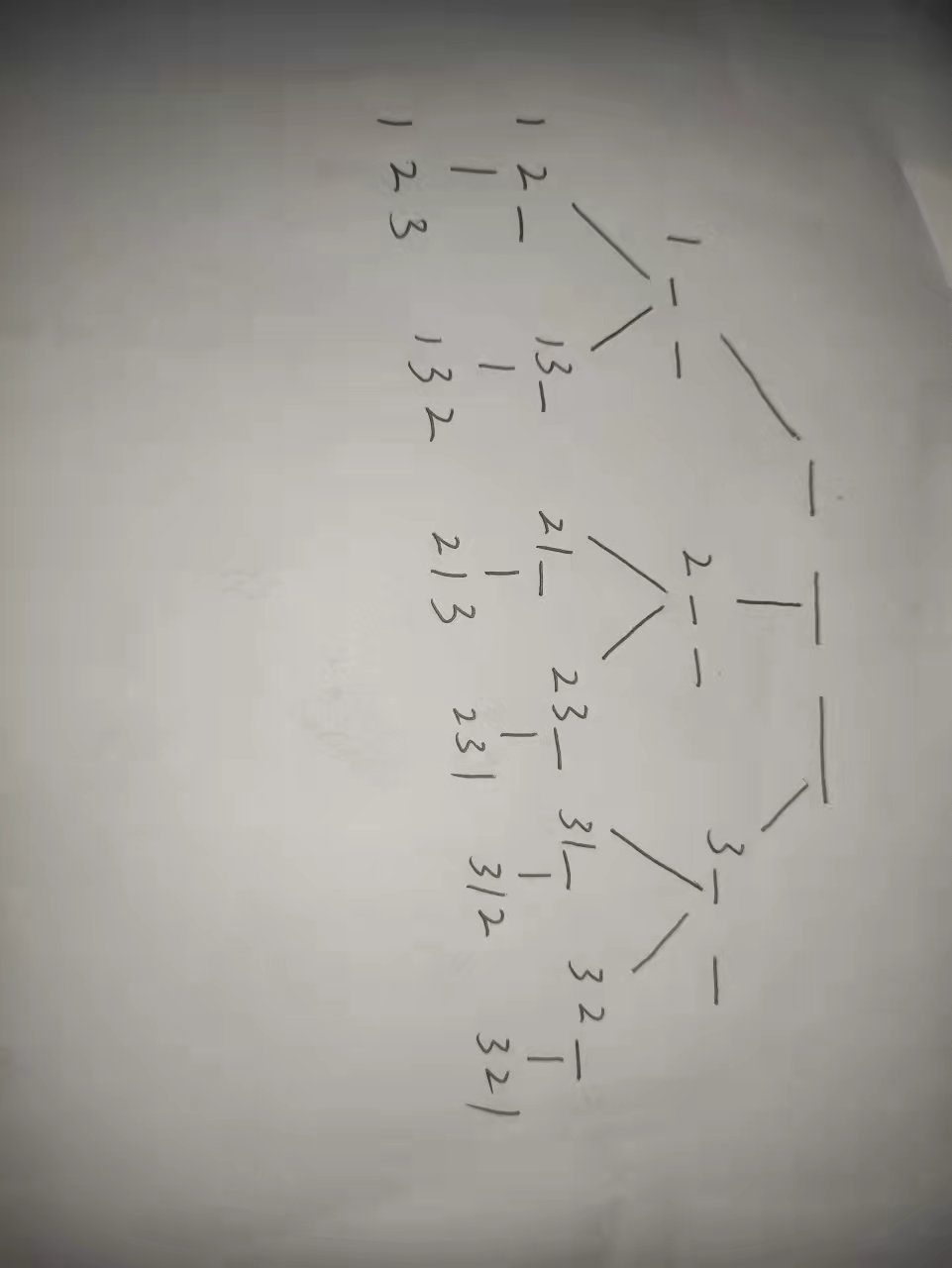
如圖所示 ：對一個位置進行查找，把之前沒有用過的數填上去，接著對下一個位置進行

相同操作，知道每個位置填滿數為止。

程式實現

我們總結一下在上一部分中的思路在程式中如何實現。

先定義兩個數組，一個是用來存放解的，一個是用來標記該數是否用過。

我們可以先寫一個用於列印的函數print()，每當深搜時找到一個符合條件的解時，則

print()一下，輸出這個解（註意題目輸出要求）。

接下來就是寫深搜的函數了。主要思路：先判斷格子是否填滿了，如果填滿，則print()一下。

如果沒有填滿，則開始迴圈，在迴圈中先判斷當前填的數是否用過，如果沒有，則填

入，搜索下一格。

代碼如下

#include <iostream>
using namespace std;
const int  N = 10;
int n;
int a[N];
bool q[N];
void dfs(int x){
	if(x == n){
		for(int i = 0 ; i < n ; i++)
		printf("%5d",a[i]);
		puts("");
	}
	for(int i = 1 ; i <= n ; i++){
		if( !q[i] ){
			a [x] = i;
			q[i] = true ;
			dfs(x+1);
			q[i] = false ;
			a[x] = 0;
  		}
	}
}
int main()
{
	cin >> n ;
	
	dfs(0);
	
	return 0;
	
	
 }