最小生成樹(貪心演算法) 概念 一個有 n 個結點的連通圖的生成樹是原圖的極小連通子圖,且包含原圖中的所有 n 個結點,並且有保持圖連通的最少的邊。 連通圖有多種連接方式,而其中最小的連通圖,就是最小生成樹 連通圖分為:無向、有向 無向連通圖:所以頂點相連,但各個邊都沒有方向 有向連通圖:邊有方向 1 ...
最小生成樹(貪心演算法)
概念
- 一個有 n 個結點的連通圖的生成樹是原圖的極小連通子圖,且包含原圖中的所有 n 個結點,並且有保持圖連通的最少的邊。
- 連通圖有多種連接方式,而其中最小的連通圖,就是最小生成樹
- 連通圖分為:無向、有向
- 無向連通圖:所以頂點相連,但各個邊都沒有方向
- 有向連通圖:邊有方向
1.普利姆演算法(Prim)-----最近頂點策略
-
策略:選擇圖中的一個頂點作為起始點,每一步貪心選擇不在當前生成樹中的最近頂點加入生成樹中,直到所有頂點都加入到樹中。
-
演算法如下:
(1)、假如G為無向連通帶權圖,每兩個相鄰節點構成一個帶權邊,其值設為:權值。即:(所有每相鄰的兩個節點都有各自的權值,只是權值大小不同)
(2)、設集合 W和D,W用於存放G的最小生成樹的頂點集合,D存放G的最小生成樹的權值集合
(3)、選中G的一個節點 (其索引為data-0) 作為初值,從頂點data0開始構建最小生成樹。集合D的初值為D{}。
(4)、標記W[data0]=1.表示標記已被選中的節點
(5)、data0節點找出周圍相鄰,且帶權邊最小的節點(其索引為data-n)。
(6)、將節點data-n加入集合W。標記W[data-n]=1;將帶權邊(data0,data-n)加入集合D
(7)、重覆上面步驟
-
圖解步驟:
(1)、無向連通圖

(2)、以節點A開始延申:發現(A,G)間的權值最小,於是選中G為連通點

(3)、以A、G節點為頂點找與之相鄰的最小權值邊:發現(G,B)間的帶權邊值最小,選中B
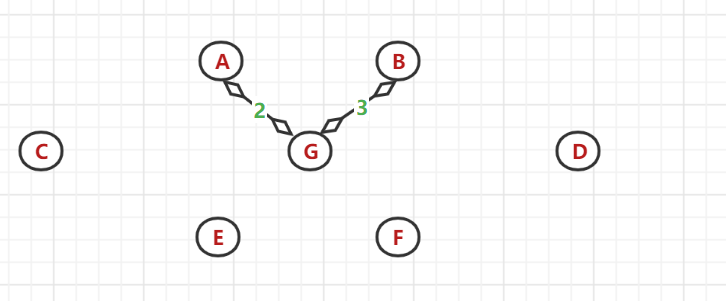
(4)、又以 A、G、B節點為頂點找與之相鄰的最小權值邊:發現(G,E)間的帶權邊值最小,選中E
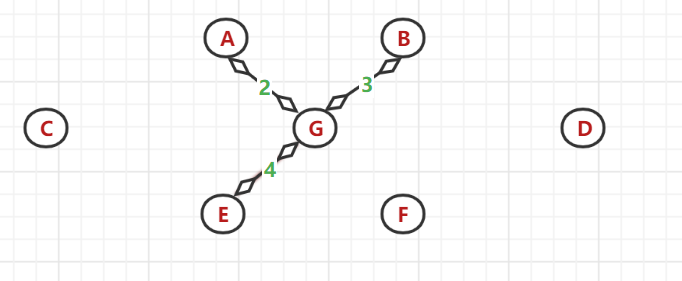
(5)、又以 A、G、B、E節點為頂點找與之相鄰的最小權值邊:發現(B,A)與(E,F)間的帶權邊值最相同且最小,但A和B節點都是已使用過的節點,所以選中 F 節點

(6)、依次選擇,得到最後的最小生成樹

代碼如下:
import java.util.Arrays;
/*
貪心策略:最小生成樹-普里姆演算法
:在包含n個頂點的無向連通圖中,找出只有(n-1)條邊且包含n個頂點的連通子圖。使其形成最小連通子圖。連通子圖不能出現迴路
分析:
1.設置集合 W和集合 D 。其中W存入的是無向連通圖中最小生成樹的頂點集合;D存入的是最小生成樹每相鄰兩個頂點之間的連接邊的集合
2.另集合W的初值為 W{w0}(即從w0頂點開始構建最小生成樹),另集合D初始值為 D{}
3.設V為還未被選中的頂點。
4.從w與v=V-W 中組成的所有帶權邊中選出最小的帶權邊(wn,vn).
5.將頂點vn加入集合W中。此時集合W{wn,vn},集合D{(wn,vn)}
6.重覆上面步驟,直到V中所有頂點都加入到了W中,邊有n-1條帶權邊。結束
代碼:探討修路問題
*/
public class test1 {
public static void main(String[] args) {
//所有節點
char[] ndata=new char[]{'A','B','C','D','E','F','G'};
//獲取節點個數
int nodes = ndata.length;
//鄰接矩陣.用較大的數10000表示兩點不連通
int[][] ndlenght=new int[][]{
//A ,B,C, D , E , F ,G
{10000,5,7,10000,10000,10000,2}, //A
{5,10000,10000,9,10000,10000,3}, //B
{7,10000,10000,10000,8,10000,10000},//C
{10000,9,10000,10000,10000,4,10000},//D
{10000,10000,8,10000,10000,5,4}, //E
{10000,10000,10000,4,5,10000,6}, //F
{2,3,10000,10000,4,6,10000}, //G
};
//創建圖對象
Chart chart=new Chart(nodes);
//創建生成數對象
MinTree mt=new MinTree();
//創建鄰接矩陣
mt.creathart(chart,nodes,ndata,ndlenght);
//獲取矩陣
// mt.dischart(chart);
mt.Prim(chart,0);
}
}
/*
第二步:
創建生成樹對象
*/
class MinTree{
/**
* 創建鄰接矩陣
* @param chart :圖對象
* @param nodes :節點個數
* @param ndata :存放節點數據
* @param ndlenght :帶權邊
*/
public void creathart(Chart chart,int nodes,char[] ndata,int[] [] ndlenght){
//i:已經被選中的節點,ndata[i0]就是為初值,ndata[0]節點開始生成樹。一共有nodes個
for (int i=0;i<nodes;i++){
//將當前已被選的節點存入圖對象的ndata中
chart.ndata[i]=ndata[i];
//j:還未被選中的節點
for (int j=0;j<nodes;j++){
//將所有可能兩兩連接的節點組合,存入圖對象的鄰接矩陣中
chart.ndlenght[i][j]=ndlenght[i][j];
}
}
}
//顯示圖矩陣
public void dischart(Chart chart){
for (int[] link:chart.ndlenght){
System.out.println(Arrays.toString(link));
}
}
/**
* 普里姆演算法:
* 最小生成樹
* @param chart:圖
* @param v :初值
*/
public void Prim(Chart chart,int v){
//存放已被選中的節點,初始都為0
int[] ondata=new int[chart.nodes];
//標記初值節點已被選中,1(表示被選中了的)
ondata[v]=1;
//設即將相連的兩個節點下標為 index1、index2。由於還沒有存入,所以初始為-1
int index1=-1;
int index2=-1;
//由於還不知道第一個邊長為多少,所以先虛擬設置一個最大帶權邊長。後面後被替換的
int max=10000;
//k:表示最多生成(n-1)條帶權邊
for (int k=1;k<chart.nodes;k++){
//i:表示以被選中的節點;j:還未被選中的節點
for (int i=0;i<chart.nodes;i++){
for (int j=0;j<chart.nodes;j++){
if (ondata[i]==1&&ondata[j]==0&&chart.ndlenght[i][j]<max){
max=chart.ndlenght[i][j];
index1=i;
index2=j;
}
}
}
System.out.println("節點:<"+chart.ndata[index1]+","+chart.ndata[index2]+">,==>帶權邊長:"+max);
//將當前節點標記為以訪問使用的節點
ondata[index2]=1;
//重置max
max=10000;
}
}
}
/*
第一步:
創建圖對象
*/
class Chart{
int nodes; //圖中節點個數
char[] ndata; //存放節點數據
int[] [] ndlenght; //存放帶權邊。也是鄰接矩陣
//構造器
public Chart(int nodes) {
this.nodes = nodes;
//初始化,數組長度為nodes(節點個數)
ndata=new char[nodes];
//初始化,矩陣為nodes行nodes列
ndlenght=new int[nodes][nodes];
}
}
結果:

2.,克魯斯卡爾演算法(Kruskal)----最短邊策略
-
策略:每一次貪心的選擇從剩下的邊中最小的邊且不產生環路的,加入到已選邊的集合中。直到所有頂點都加入進來。
-
按照權值從小到大選擇n-1條邊,並且這些邊不構成環路。
-
演算法如下:
(1)、構建有n個頂點的無邊連通圖 W ,
(2)、對無向連通圖 H 中的各個帶權邊從小到大排序
(3)、依次從小到大將 H 中的帶權邊加入到 W中(期間不能構成環路)
-
演算法圖解及判斷環路:
-
環路:已加入加入到無邊聯通圖中的頂點的終點不能相同
-
終點:將所有頂點從小到大排序後,某個頂點的終點就是"與它相連的最大的頂點";
-
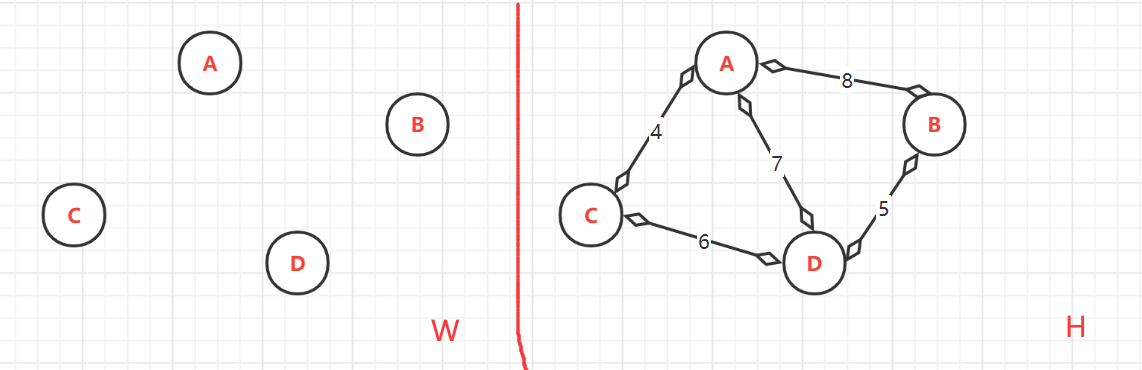
(1)、無邊連通圖 W。與無向連通圖 H(1:頂點以排序;2.權值以排序)
- 頂點的終點:此時由於還沒有加入。所以W中所有的各個頂點的終點是自己本身
-
-
(2)、將H中從小到大排序後的邊依次加入 W中。
-
(2.1)、第一次:<A,C>=4,
-
頂點的終點:因為頂點是已排序為{A,B,C,D},而目前加入到W中的只有{A,C}。所以A與C連通的最大頂點是:A--->C;C--->C
-
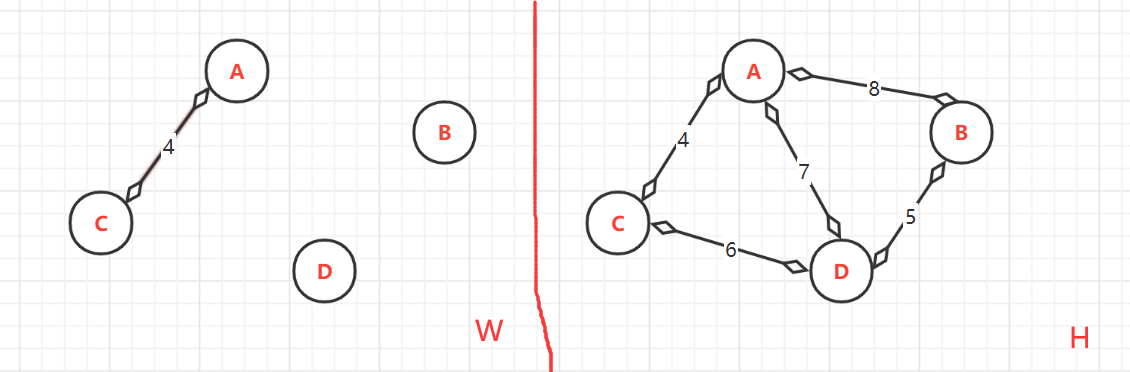
- (2.2)、第二次:<B,D>=5,
- 頂點的終點:此時**W**中有{A,C},{B,D}。由於目前{B,D}還沒有與{A,C}連通,所以B與D連通的最大頂點是:B--->D;D--->D,
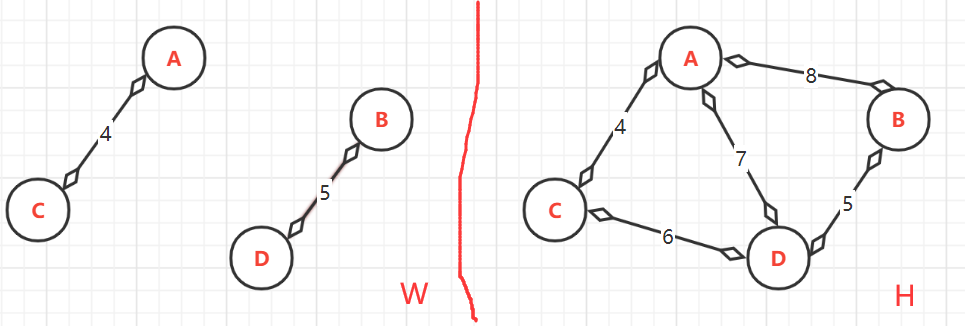
- (2.3)、第三次:<C,D>=6,這裡雖然前面C與D被加入過,但它們的終點卻不同。
- 頂點的終點:此時**W**中有{A,C},{B,D},{C,D}。由於{C,D}的加入導致{A,B,C,D}相互連接,所最大頂點是:A--->D;B--->D;C--->D;D--->D,
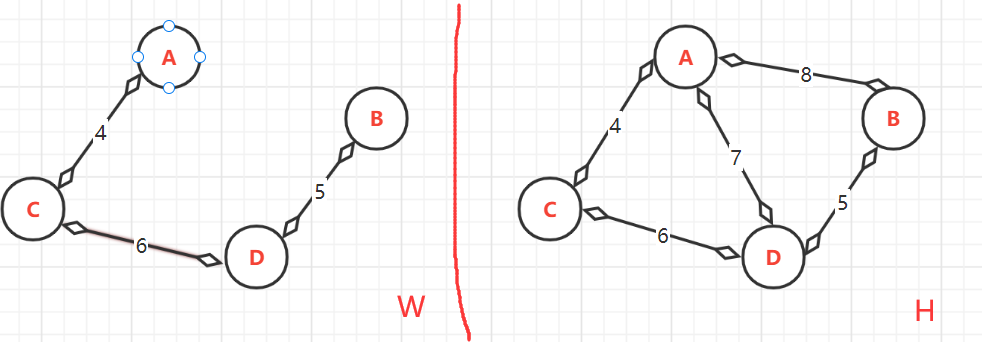
- (2.4)、第四次:<A,D>=7。由於前面得出A,與D的最大頂點(終點)相同為D,如果加入會構成環路。所以不能加入.跳過此邊,加入下一條邊
- (2.5)、第五次:<A,B>=8。由於前面得出A,與B的最大頂點(終點)相同為D,如果加入會構成環路。所以不能加入。所以加入下一條邊,發現沒有,所有邊都已加入到了。
-
(3)、註意:在(2.3)時。其實所有頂點都已加入到了W中,所以就不需要判斷後面的了。後面的結論只是為了說明終點與環路。
-
代碼如下:
import java.util.Arrays;
/**
* 最小生成樹:克魯斯卡爾演算法
* 將無向連通圖中的各個邊從小到大排序,依次放入無邊連通圖中(不能出現環路)
*/
public class test1 {
private int geshu; //邊的個數
private char[] data; //存放節點
private int[][] allquanzhi; //存放帶權邊,鄰接矩陣
//標記不能相連通的兩個節點,即不相鄰的兩個節點所形成的帶權邊。為Integer最大值
private static final int maxlen = Integer.MAX_VALUE;
public static void main(String[] args) {
// char[] data={'A','B','C','D','E'};
// int[][] allquanzhi={
// {0,20,maxlen,60,15},
// {20,0,42,maxlen,maxlen},
// {maxlen,42,0,30,maxlen},
// {60,maxlen,30,0,23},
// {15,maxlen,maxlen,23,0},
// };
char[] data={'A','B','C','D'};
int[][] allquanzhi={
{0,8,4,7},
{8,0,maxlen,5},
{4,maxlen,0,6},
{7,5,6,0}
};
test1 t=new test1(data,allquanzhi);
//列印矩陣
t.dayinjuzheng();
Bian[] bians=t.andbian();
System.out.println("排序前的邊集合"+Arrays.toString(bians));
t.biansort(bians);
System.out.println("排序後的邊集合"+Arrays.toString(bians));
t.KrusKal();
}
//定義構造器
public test1(char[] data, int[][] allquanzhi) {
//初始化頂點數
int spotgeshu = data.length;
//初始化頂點(節點)
this.data = data;
//初始化 邊
this.allquanzhi = allquanzhi;
//統計邊的個數
for (int i = 0; i < spotgeshu; i++) {
for (int j = i+1; j < spotgeshu; j++) {
if (this.allquanzhi[i][j] < maxlen) {
geshu++;
}
}
}
}
//列印鄰接矩陣
public void dayinjuzheng() {
System.out.println(geshu);
for (int i = 0; i < data.length; i++) {
for (int j = 0; j < data.length; j++) {
//格式化輸出
System.out.printf("%15d\t", +allquanzhi[i][j]);
}
System.out.println();
}
}
/*
對邊排序:冒泡《從小到大》
*/
public void biansort(Bian[] bian){
for (int i=bian.length-1;i>0;i--){
for (int j=0;j<i;j++){
if (bian[j].bianquanzhi>bian[j+1].bianquanzhi){
Bian temp=bian[j];
bian[j]=bian[j+1];
bian[j+1]=temp;
}
}
}
}
/*
判斷頂點是否存在
返回頂點的索引
*/
public int ismbian(char ch){
for (int i=0;i<data.length;i++){
if (data[i]==ch){
return i;
}
}
//如果ch不是頂點就返回-1
return -1;
}
/*
將所以相鄰邊存入Bian[]中
*/
public Bian[] andbian(){
int index=0;
Bian[] bians=new Bian[geshu];
for (int i=0;i<data.length;i++){
for (int j=i+1;j<data.length;j++){
if (allquanzhi[i][j]!=maxlen){
bians[index++]=new Bian(data[i],data[j],allquanzhi[i][j]);
}
}
}
return bians;
}
/*
獲取小標為i的頂點的終點,用於判斷兩個頂點的終點是否相同
star:存入的是頂點的終點的索引,初始化為{0,0,0,0,...},
i:頂點的索引
*/
public int getEnd(int[] star,int i){
//動態的判斷以此頂點的索引,
//相連的前一個頂點的終點索引就是後一個頂點的索引
//由於第一次的頂點的終點是自己的索引都
//如果在star中找到了終點
while (star[i]!=0){
//就將此終點的值變為新的頂點的索引(找到此索引對應的頂點的終點,直到新的索引在star中沒有找到終點,即為0,就將此索引返回為最初始的節點的終點索引)
i=star[i];
}
//返回為終點
return i;
}
/*
最小生成樹克魯斯卡爾演算法
*/
public void KrusKal(){
int index=0; //最後結果數組的索引
//存放最小生成樹每個頂點的終點
int[] star=new int[geshu];
//保存最終生成樹
Bian[] fin=new Bian[geshu];
//獲取邊的集合
Bian[] andnewbian = andbian();
//對所有邊進行排序
biansort(andnewbian);
//遍歷邊集合。在判斷的同時判斷是否形成迴路
for (int i=0;i<geshu;i++){
//上面andbian存放獲得的邊的類:bians[index++]=new Bian(data[i],data[j],allquanzhi[i][j]);
//獲取第一邊的起點(頂點),對應的是data[i]
int h1=ismbian(andnewbian[i].da1);
//獲取第一條邊的第二個頂點,對應的是data[j]
int h2=ismbian(andnewbian[i].da2);
//獲取第一個頂點的終點
int end = getEnd(star, h1);
//獲取第二個頂點的終點
int end1 = getEnd(star, h2);
//判斷迴路:如果沒有構成迴路
if (end!=end1){
//設置end1為已有生成數的終點
star[end]=end1;
//此時最終生成樹有了一條邊
fin[index++]=andnewbian[i];
}
}
System.out.println("最後生成樹:"+Arrays.toString(fin));
System.out.println("最小生成樹:");
for (int i=0;i<index;i++){
System.out.println(fin[i]);
}
}
}
/*
邊類
*/
class Bian{
//組成一條邊的兩個節點
char da1;
char da2;
//邊權值
int bianquanzhi;
public Bian(char da1, char da2, int bianquanzhi) {
this.da1 = da1;
this.da2 = da2;
this.bianquanzhi = bianquanzhi;
}
@Override
public String toString() {
return "bian{" +
"da1=" + da1 +
", da2=" + da2 +
", bianquanzhi=" + bianquanzhi +
'}';
}
}
結果:




