BLOG-2_ZenDei技術網路在線

BLOG-2 （1）前言：總結之前所涉及到的知識點、題量、難度等情況題目集4：知識點：類與對象、字元串方法調用、正則表達式題量：多難度：難題目集5：知識點：類與對象、字元串方法調用、正則表達式題量：多難度：難期中考試：知識點：類設計、繼承與多態、容器類題量：少難度：低（2）設計 ...

BLOG-2

（1）前言：

　　總結之前所涉及到的知識點、題量、難度等情況

　　題目集4：知識點：類與對象、字元串方法調用、正則表達式題量：多難度：難

　　題目集5：知識點：類與對象、字元串方法調用、正則表達式題量：多難度：難

　　期中考試：知識點：類設計、繼承與多態、容器類題量：少難度：低

（2）設計與分析：

　　重點對題目的提交源碼進行分析，可參考SourceMonitor的生成報表內容以及PowerDesigner的相應類圖，要有相應的解釋和心得（做到有圖有真相），本次Blog必須分析PTA中的圖形類設計的題目、超星中鏈表類練習題目以及期中考試的三道題目

PTA題目集4（四邊形）

7-1 sdut-String-2 識蛟龍號載人深潛，立科技報國志（II）（正則表達式）

‘蛟龍’號是我國載人深潛發展歷程中的一個重要里程碑。它不只是一個深海裝備，更代表了一種精神，一種不畏艱險、趕超世界的精神，它是中華民族進軍深海的號角。

瞭解蛟龍號”載人深潛器“的驕人業績，為我國海底載人科學研究和資源勘探能力達到國際領先水平而自豪，小伙伴們與祖國同呼吸、共命運，一定要學好科學文化知識、提高個人能力，增強創新意識，做事精益求精，立科技報國之志！

請編寫程式，實現如下功能：讀入關於蛟龍號載人潛水器探測數據的多行字元串，從給定的信息找出數字字元，輸出每行的數字之和。

提示若輸入為“2012年2月”，則該行的輸出為：2014。若幹個連續的數字字元作為一個整體，以十進位形式相加。

輸入格式:

讀入關於蛟龍號載人潛水器探測數據的多行字元串，每行字元不超過80個字元。

以"end"結束。

輸出格式:

與輸入行相對應的各個整數之和。

我的代碼：

 1 import java.util.Scanner;
 2 import java.util.regex.Matcher;
 3 import java.util.regex.Pattern;
 4 
 5 public class Main
 6 {
 7     public static void main(String[] args)
 8     {
 9 
10         Scanner input = new Scanner(System.in);
11         String s = input.nextLine();
12 
13         while(!s.equals("end"))
14         {
15         String ST = "\\d+";
16         Pattern x = Pattern.compile(ST);
17         Matcher g = x.matcher(s);
18         int sum = 0;
19         while(g.find())
20         {
21             int q = Integer.parseInt(g.group());
22             sum = sum + q;
23         }
24          System.out.println(sum);
25          s = input.nextLine();
26         }
27     }
28 }

View Code

SourceMonitor的生成報表內容：

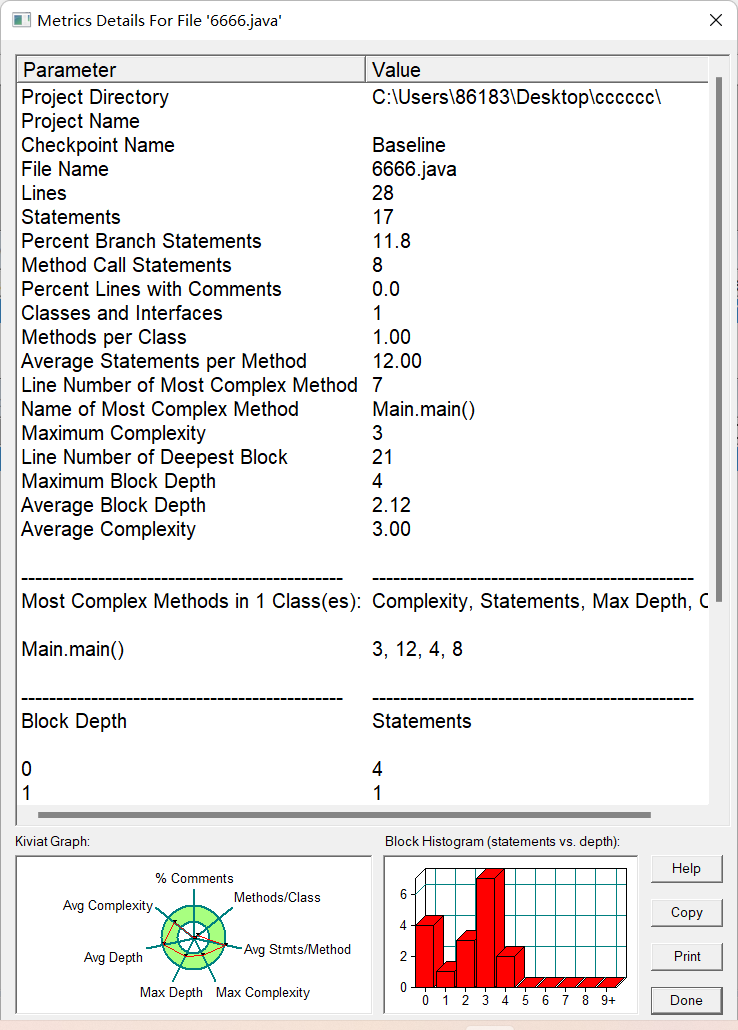
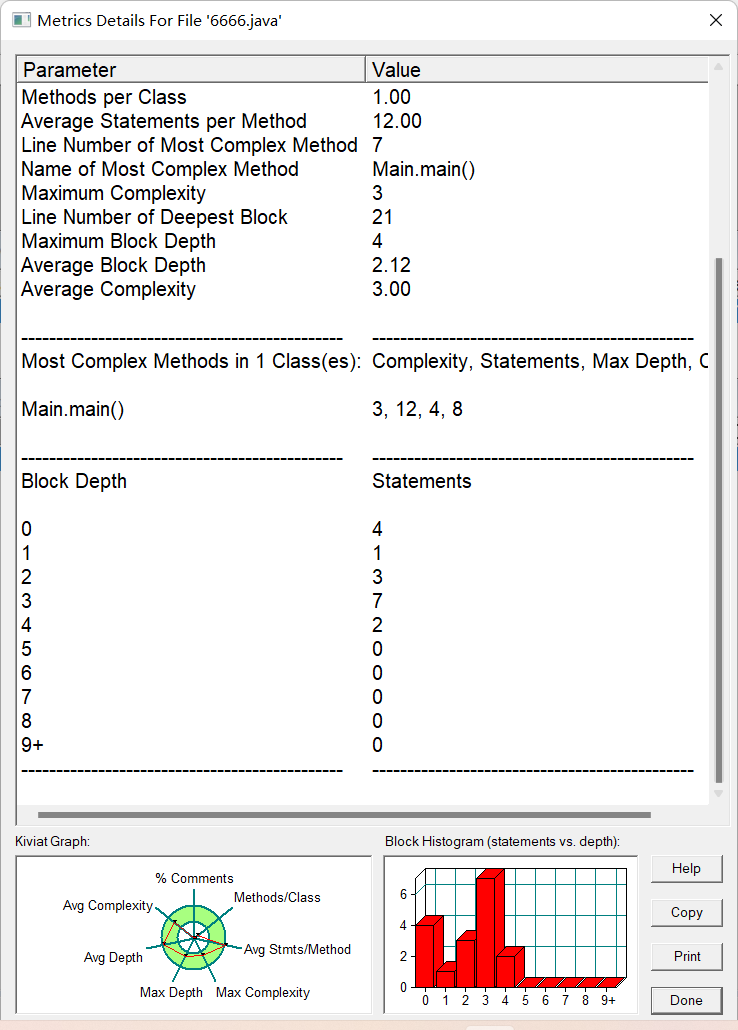
PowerDesigner的相應類圖：

分析解釋和心得：

這題需要用到Pattern和Matcher，需要掌握Pattern和Matcher。

7-2 點線形系列4-凸四邊形的計算

用戶輸入一組選項和數據，進行與四邊形有關的計算。
以下四邊形頂點的坐標要求按順序依次輸入，連續輸入的兩個頂點是相鄰頂點，第一個和最後一個輸入的頂點相鄰。
選項包括：
1：輸入四個點坐標，判斷是否是四邊形、平行四邊形，判斷結果輸出true/false，結果之間以一個英文空格符分隔。
2：輸入四個點坐標，判斷是否是菱形、矩形、正方形，判斷結果輸出true/false，結果之間以一個英文空格符分隔。若四個點坐標無法構成四邊形，輸出"not a quadrilateral"
3：輸入四個點坐標，判斷是凹四邊形（false）還是凸四邊形(true)，輸出四邊形周長、面積，結果之間以一個英文空格符分隔。若四個點坐標無法構成四邊形，輸出"not a quadrilateral"
4：輸入六個點坐標，前兩個點構成一條直線，後四個點構成一個四邊形或三角形，輸出直線與四邊形（也可能是三角形）相交的交點數量。如果交點有兩個，再按面積從小到大輸出四邊形(或三角形)被直線分割成兩部分的面積（不換行）。若直線與四邊形或三角形的一條邊線重合，輸出"The line is coincide with one of the lines"。若後四個點不符合四邊形或三角形的輸入，輸出"not a quadrilateral or triangle"。
後四個點構成三角形的情況：假設三角形一條邊上兩個端點分別是x、y，邊線中間有一點z，另一頂點s：
1）符合要求的輸入：頂點重覆或者z與xy都相鄰，如x x y s、x z y s、x y x s、s x y y。此時去除冗餘點，保留一個x、一個y。
2) 不符合要求的輸入：z 不與xy都相鄰，如z x y s、x z s y、x s z y
5：輸入五個點坐標，輸出第一個是否在後四個點所構成的四邊形（限定為凸四邊形，不考慮凹四邊形）或三角形（判定方法見選項4）的內部（若是四邊形輸出in the quadrilateral/outof the quadrilateral，若是三角形輸出in the triangle/outof the triangle）。如果點在多邊形的某條邊上，輸出"on the triangle或者on the quadrilateral"。若後四個點不符合四邊形或三角形，輸出"not a quadrilateral or triangle"。

輸入格式:

基本格式：選項+":"+坐標x+","+坐標y+" "+坐標x+","+坐標y。點的x、y坐標之間以英文","分隔，點與點之間以一個英文空格分隔。

輸出格式:

基本輸出格式見每種選項的描述。
異常情況輸出：
如果不符合基本格式，輸出"Wrong Format"。
如果符合基本格式，但輸入點的數量不符合要求，輸出"wrong number of points"。
註意：輸出的數據若小數點後超過3位，只保留小數點後3位，多餘部分採用四捨五入規則進到最低位。小數點後若不足3位，按原始位數顯示，不必補齊。例如：1/3的結果按格式輸出為 0.333，1.0按格式輸出為1.0

選項1、2、3中，若四邊形四個點中有重合點，輸出"points coincide"。
選項4中，若前兩個輸入線的點重合，輸出"points coincide"。

我的部分核心源碼

  1        static point A;
  2        static point B;
  3        static point C;
  4        static point D;
  5        static point E;
  6        static point F;
  7        static line AB;
  8        static line BC;
  9        static line CD;
 10        static line DA;
 11        static line AC;
 12        static line BD;
 13        static line EF;
 14 
 15        public static boolean isTri() //四點是否構成為三角形
 16        {
 17            return (!B.twoCoin(D)&&!BD.online(A)&&!BD.online(C)&&A.twoCoin(C) ) || ( !A.twoCoin(C)&&!AC.online(B)&&!AC.online(D)&&B.twoCoin(D) ) || ( !B.twoCoin(D)&&BD.OnLineSegment(A)&&!BD.online(C) ) || ( !A.twoCoin(C)&&AC.OnLineSegment(B)&&!AC.online(D) ) || ( !B.twoCoin(D)&&BD.OnLineSegment(C)&&!BD.online(A) ) || ( !A.twoCoin(C)&&AC.OnLineSegment(D)&&!AC.online(B) ) ;
 18        }
 19 
 20 
 21        public static boolean isRec()  //是否為矩形
 22        {
 23            return isPara()&&A.twolength(C)==B.twolength(D);
 24        }
 25 
 26        public static double[] splitDate(String a)//String型坐標轉為double型坐標
 27        {
 28            int c = 0,i = 0;
 29            Pattern p = Pattern.compile("(-?\\d*)\\.?\\d+");  //正則表達式
 30            Matcher m = p.matcher(a);
 31 
 32            while (m.find())
 33                c++;
 34 
 35            double[] array = new double[c-1];
 36            Matcher m2 = p.matcher(a);
 37 
 38            while (m2.find())
 39            {
 40                if(i>0)
 41                    array[i-1] = Double.parseDouble(m2.group(0));
 42                i++;
 43            }
 44            return array;
 45        }
 46 
 47        public static boolean isPara()//是否為平行四邊形
 48        {
 49            return isQuad()&&AB.Slope().equals(CD.Slope())&&A.twolength(B)==C.twolength(D)&&BC.Slope().equals(DA.Slope())&&B.twolength(C)==D.twolength(A);
 50        }
 51 
 52 
 53        public static boolean isDia() //是否為菱形
 54        {
 55            return isPara()&&A.twolength(B)==B.twolength(C);
 56        }
 57 
 58        public static void dividedArea(line L, point p1,point p2,point p3) //直線切三角形交點個數及切割面積
 59        {
 60            line l12 = new line(p1, p2);
 61            line l23 = new line(p2, p3);
 62            line l13 = new line(p1, p3);
 63 
 64            if(L.threeSameplace(p1, p2, p3))
 65                System.out.println(0);
 66            else if(( L.online(p1)&&L.twoSameplace(p2, p3) )||( L.online(p2)&&L.twoSameplace(p1, p3) ) ||( L.online(p3)&&L.twoSameplace(p1, p2) ) )
 67                System.out.println(1);
 68            else if(L.firstPointelseTwoPoints(p1, p2, p3) )
 69                dateCompare( triArea(p1, L.twoInter(l12), L.twoInter(l13) ), triArea(p1, p2, p3)-triArea(p1, L.twoInter(l12), L.twoInter(l13) ) );
 70            else if(L.firstPointelseTwoPoints(p2, p1, p3))
 71                dateCompare( triArea(p2, L.twoInter(l12), L.twoInter(l23) ), triArea(p1, p2, p3)-triArea(p2, L.twoInter(l12), L.twoInter(l23) ) );
 72            else if(L.firstPointelseTwoPoints(p3, p1, p2))
 73                dateCompare( triArea(p3, L.twoInter(l13), L.twoInter(l23) ), triArea(p1, p2, p3)-triArea(p3, L.twoInter(l13), L.twoInter(l23) ) );
 74        }
 75 
 76 
 77        public static boolean isQuad()//是否為四邊形
 78        {
 79            return !AB.online(C)&&!AB.online(D)&&!BC.online(A)&&!BC.online(D)&&!CD.online(B)&&!CD.online(A)&&!DA.online(B)&&!DA.online(C) &&( ( AC.twoPoint(B, D)&&BD.twoPoint(A, C)&&!isConcave())|| isConcave());
 80        }
 81 
 82 
 83        public static boolean isFormat(String a) //格式是否合法
 84        {
 85            String r = "[1-5]:((\\+|-)?(0(\\.0+)?|[1-9]\\d*|[1-9]\\d*\\.\\d+|0\\.\\d*[1-9]\\d*),(\\+|-)?(0(\\.0+)?|[1-9]\\d*|[1-9]\\d*\\.\\d+|0\\.\\d*[1-9]\\d*) )*((\\+|-)?(0(\\.0+)?|[1-9]\\d*|[1-9]\\d*\\.\\d+|0\\.\\d*[1-9]\\d*),(\\+|-)?(0(\\.0+)?|[1-9]\\d*|[1-9]\\d*\\.\\d+|0\\.\\d*[1-9]\\d*)( )?)+";
 86            boolean d = a.matches(r);
 87            return d;
 88        }
 89 
 90        public static boolean isInside(point a, point a1, point a2, point a3) //點是否在三角形內
 91        {
 92            double x = a.getx(), y = a.gety(), x1 = a1.getx(), y1 = a1.gety(), x2 = a2.getx(), y2 = a2.gety(), x3 = a3.getx(), y3 = a3.gety();
 93            if(threeonline(x1,y1,x2,y2,x3,y3))
 94                return false;
 95            
 96            double c11=( (x1-x)*(y2-y1)-(x2-x1)*(y1-y) )*( (x1-x3)*(y2-y1)-(x2-x1)*(y1-y3) );
 97            double a11=( (x2-x)*(y3-y2)-(x3-x2)*(y2-y) )*( (x2-x1)*(y3-y1)-(x3-x2)*(y2-y1) );
 98            double b11=( (x3-x)*(y1-y3)-(x1-x3)*(y3-y) )*( (x3-x2)*(y1-y3)-(x1-x3)*(y3-y2) );
 99            
100            if(c11>0&&a11>0&&b11>0)
101                return true;
102            else
103                return false;
104        }

View Code

SourceMonitor的生成報表內容：

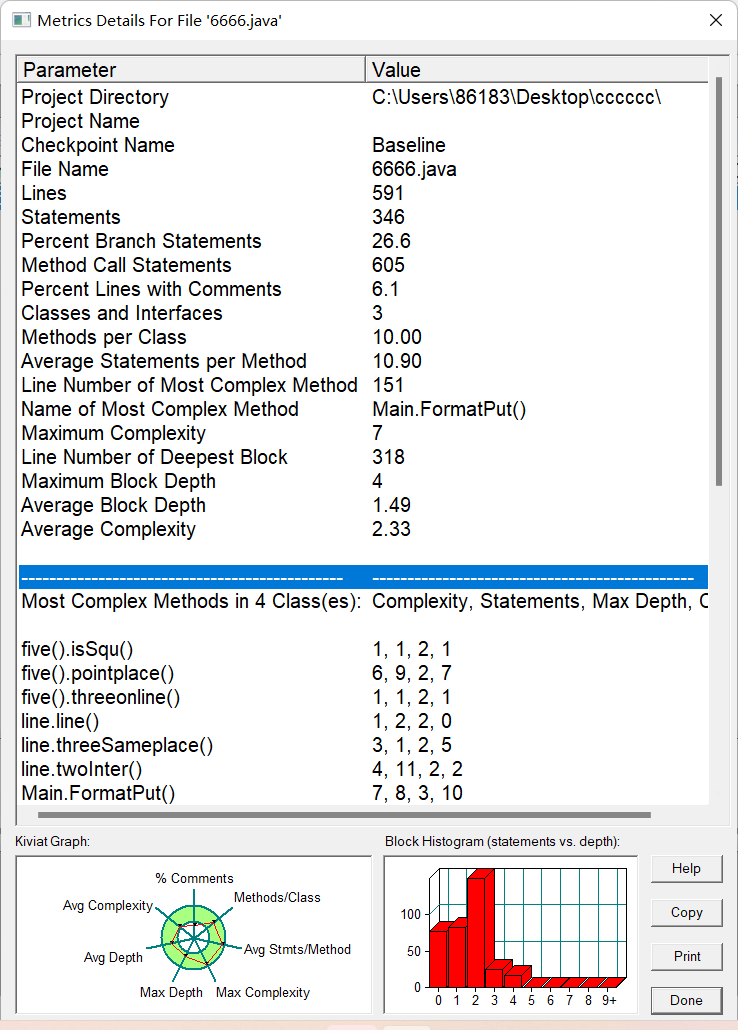
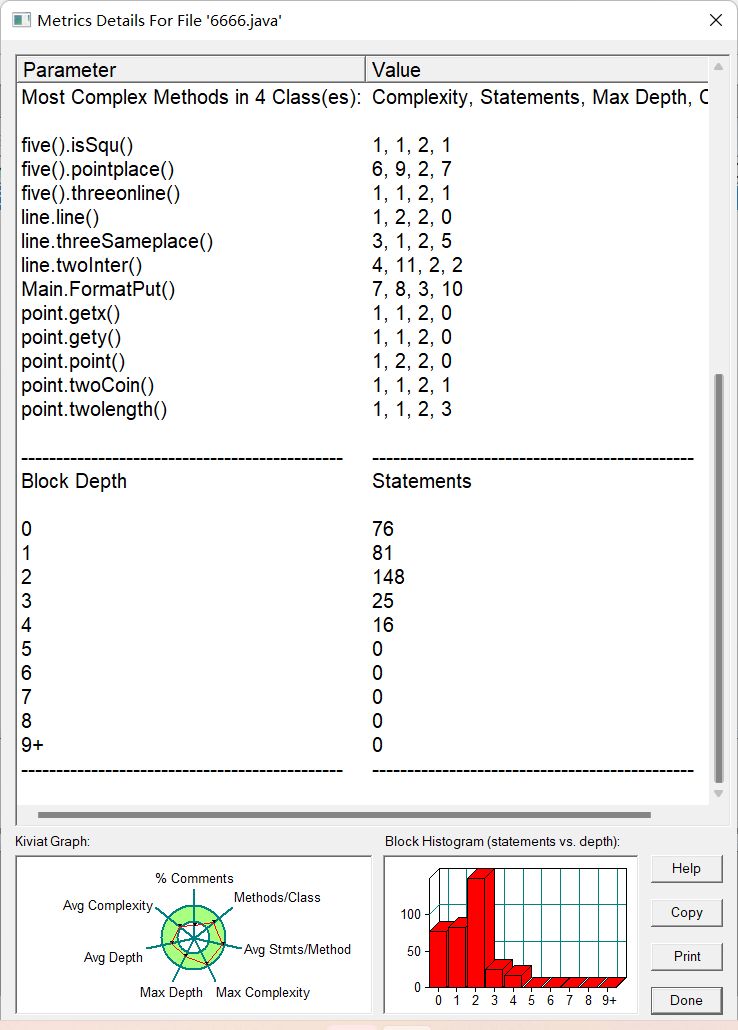
PowerDesigner的相應類圖：

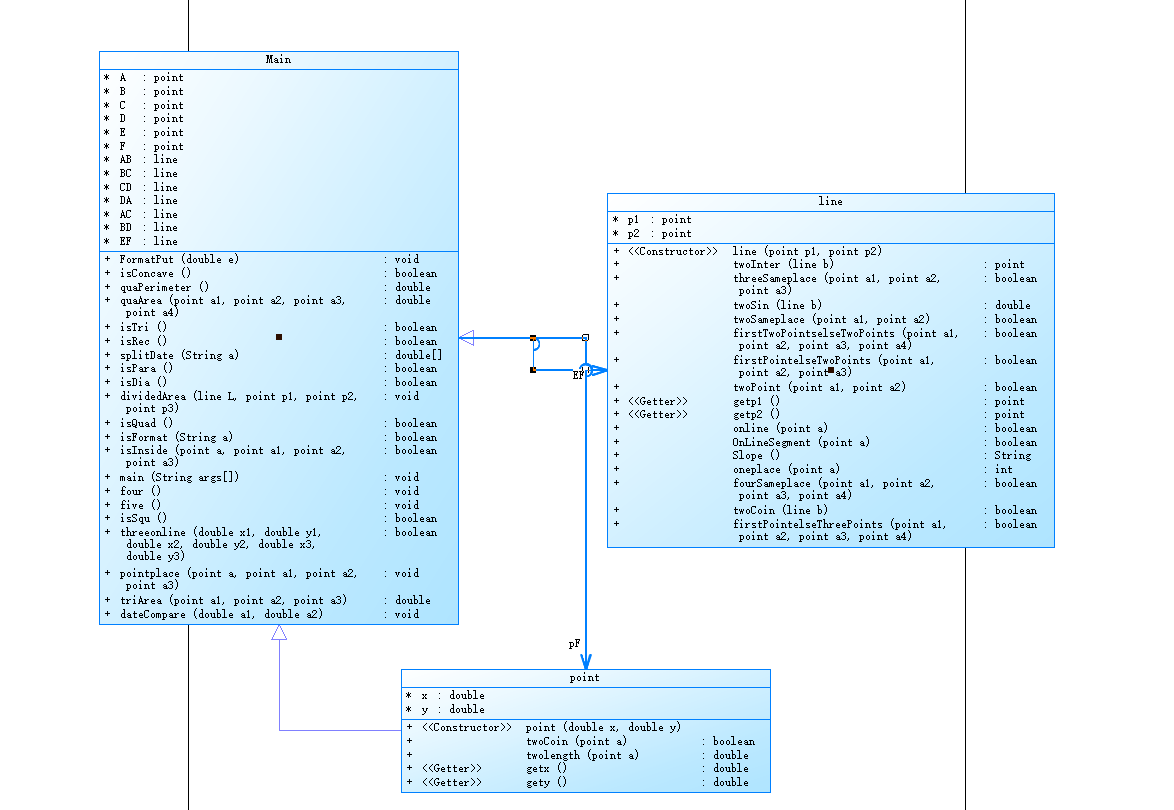
分析解釋和心得：

這題較難，主要使用點類和線類來簡化解題，以點類和線類為基礎來在主類中寫更多的解題的相關方法如判斷是否為矩形的方法，將一題分成若幹個小細節來解。另外本題也考驗數學的功力，需要知道如何求面積和分割。

7-3 設計一個銀行業務類

編寫一個銀行業務類BankBusiness，具有以下屬性和方法：
（1）公有、靜態的屬性：銀行名稱bankName，初始值為“中國銀行”。
（2）私有屬性：賬戶名name、密碼password、賬戶餘額balance。
（3）銀行對用戶到來的歡迎（welcome）動作（靜態、公有方法），顯示“中國銀行歡迎您的到來！”，其中“中國銀行”自動使用bankName的值。
（4）銀行對用戶離開的提醒（welcomeNext）動作（靜態、公有方法），顯示“請收好您的證件和物品，歡迎您下次光臨！”
（5）帶參數的構造方法，完成開戶操作。需要賬戶名name、密碼password信息，同時讓賬戶餘額為0。
（6）用戶的存款（deposit）操作（公有方法，需要密碼和交易額信息），密碼不對時無法存款且提示“您的密碼錯誤！”；密碼正確、完成用戶存款操作後，要提示用戶的賬戶餘額，例如“您的餘額有1000.0元。”。
（7）用戶的取款（withdraw）操作（公有方法，需要密碼和交易額信息）。密碼不對時無法取款且提示“您的密碼錯誤！”；密碼正確但餘額不足時提示“您的餘額不足！”；密碼正確且餘額充足時扣除交易額並提示用戶的賬戶餘額，例如“請取走鈔票，您的餘額還有500.0元。”。

編寫一個測試類Main，在main方法中，先後執行以下操作：
（1）調用BankBusiness類的welcome()方法。
（2）接收鍵盤輸入的用戶名、密碼信息作為參數，調用BankBusiness類帶參數的構造方法，從而創建一個BankBusiness類的對象account。
（3）調用account的存款方法，輸入正確的密碼，存入若幹元。密碼及存款金額從鍵盤輸入。
（4）調用account的取款方法，輸入錯誤的密碼，試圖取款若幹元。密碼及取款金額從鍵盤輸入。
（5）調用account的取款方法，輸入正確的密碼，試圖取款若幹元（取款金額大於餘額）。密碼及取款金額從鍵盤輸入。
（6）調用account的取款方法，輸入正確的密碼，試圖取款若幹元（取款金額小於餘額）。密碼及取款金額從鍵盤輸入。
（7）調用BankBusiness類的welcomeNext()方法。

輸入格式:

輸入開戶需要的姓名、密碼
輸入正確密碼、存款金額
輸入錯誤密碼、取款金額
輸入正確密碼、大於餘額的取款金額
輸入正確密碼、小於餘額的取款金額

輸出格式:

中國銀行（銀行名稱）歡迎您的到來！
您的餘額有多少元。
您的密碼錯誤！
您的餘額不足！
請取走鈔票，您的餘額還有多少元。
請收好您的證件和物品，歡迎您下次光臨！

我的源碼

 1 import java.util.Scanner;
 2 public class Main
 3 {
 4     public static void main(String[] args)
 5     {
 6         System.out.println("中國銀行歡迎您的到來！");
 7         Scanner input = new Scanner(System.in);
 8         String a = input.nextLine();
 9         String b = input.nextLine();
10         String c = input.nextLine();
11         String d = input.nextLine();
12         String e = input.nextLine();
13         String[] p = b.split(" ");
14         int m = Integer.parseInt(p[1]);
15         System.out.println("您的餘額有"+ m +".0元。");
16         System.out.println("您的密碼錯誤！");
17         System.out.println("您的餘額不足！");
18         String[] h = e.split(" ");
19         int u = Integer.parseInt(h[1]);
20         System.out.println("請取走鈔票，您的餘額還有"+ (m-u) +".0元。");
21         System.out.println("請收好您的證件和物品，歡迎您下次光臨！");
22     }
23 }

View Code

SourceMonitor的生成報表內容：

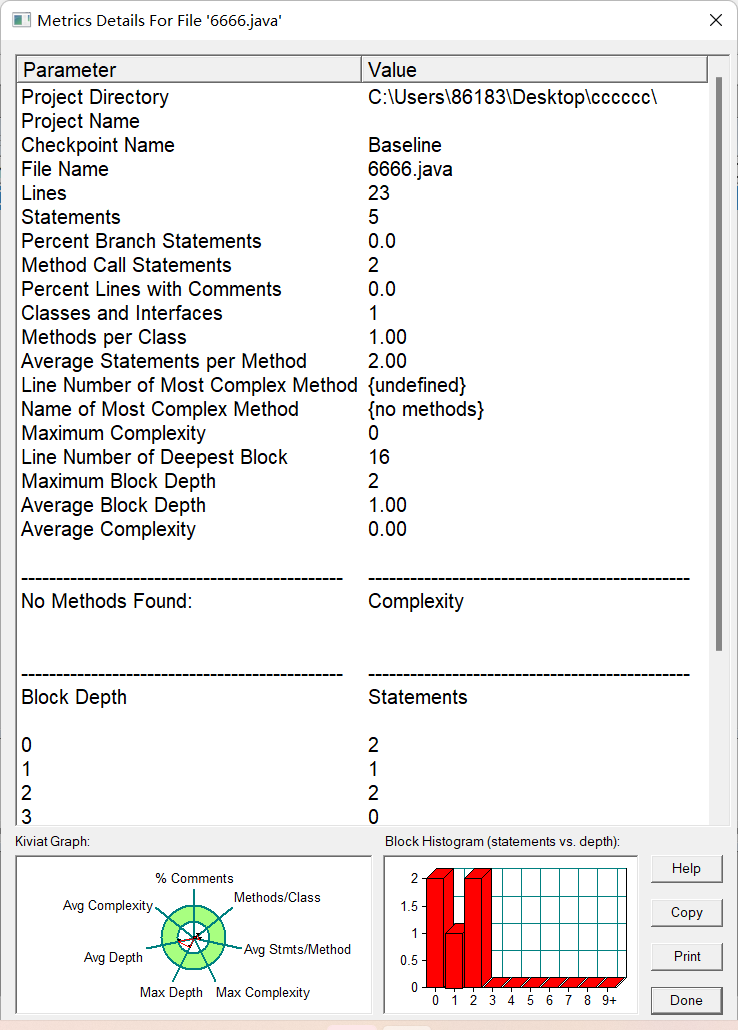
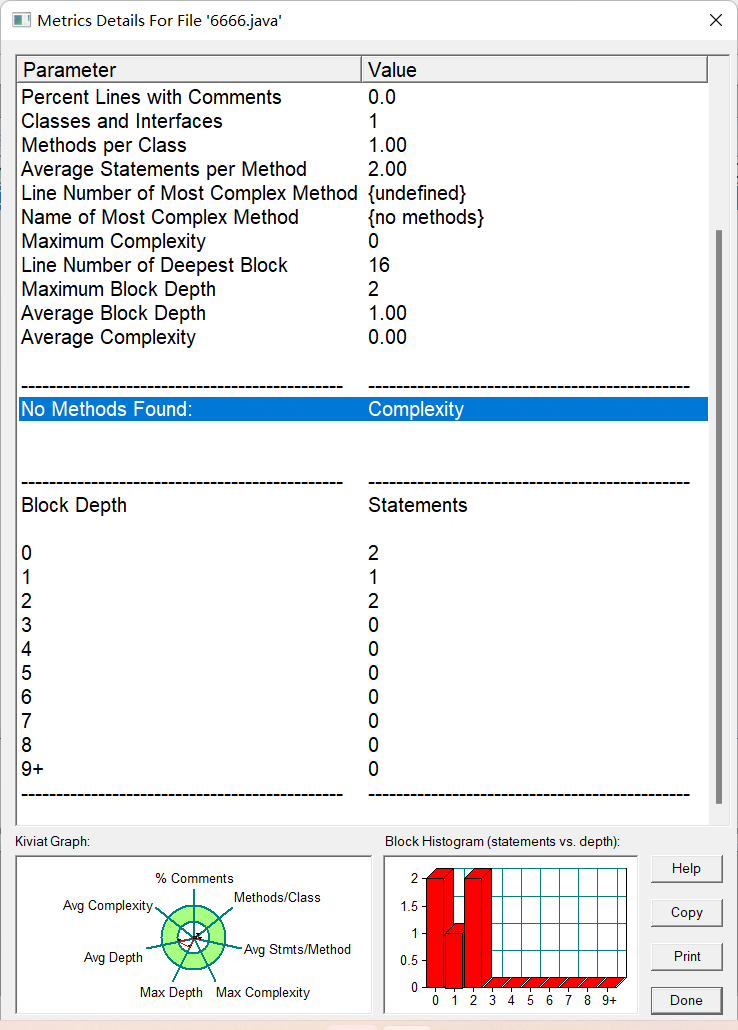
PowerDesigner的相應類圖：

分析解釋和心得：

這題是類的訓練題，但是因為測試點簡單所以我直接面向結果編程了，有時間我會再完整地寫一下。

PTA題目集5（五邊形）

7-1 點線形系列5-凸五邊形的計算-1

用戶輸入一組選項和數據，進行與五邊形有關的計算。
以下五邊形頂點的坐標要求按順序依次輸入，連續輸入的兩個頂點是相鄰頂點，第一個和最後一個輸入的頂點相鄰。
選項包括：
1：輸入五個點坐標，判斷是否是五邊形，判斷結果輸出true/false。
2：輸入五個點坐標，判斷是凹五邊形（false）還是凸五邊形(true)，如果是凸五邊形，則再輸出五邊形周長、面積，結果之間以一個英文空格符分隔。若五個點坐標無法構成五邊形，輸出"not a pentagon"
3：輸入七個點坐標，前兩個點構成一條直線，後五個點構成一個凸五邊形、凸四邊形或凸三角形，輸出直線與五邊形、四邊形或三角形相交的交點數量。如果交點有兩個，再按面積從小到大輸出被直線分割成兩部分的面積（不換行）。若直線與多邊形形的一條邊線重合，輸出"The line is coincide with one of the lines"。若後五個點不符合五邊形輸入，若前兩點重合，輸出"points coincide"。

以上3選項中，若輸入的點無法構成多邊形，則輸出"not a polygon"。輸入的五個點坐標可能存在冗餘，假設多邊形一條邊上兩個端點分別是x、y，邊線中間有一點z，另一頂點s：
1）符合要求的輸入：頂點重覆或者z與xy都相鄰，如：x x y s、x z y s、x y x s、s x y y。此時去除冗餘點，保留一個x、一個y。
2) 不符合要求的輸入：z不與xy都相鄰，如：z x y s、x z s y、x s z y

輸入格式:

基本格式：選項+":"+坐標x+","+坐標y+" "+坐標x+","+坐標y。點的x、y坐標之間以英文","分隔，點與點之間以一個英文空格分隔。

輸出格式:

我的部分核心源碼

  1 public double isPentagon(Point a,Point b,Point c) {
  2     double q=a.x-b.x;
  3     double w=a.y-b.y;
  4     double e=c.x-b.x;
  5     double r=c.y-b.y;
  6     double s=Math.sqrt(q * q + w * w);
  7     double t=Math.sqrt(e * e + r * r);
  8     double f=q * e + w * r;
  9     double v = f /(s*t); 
 10     double k=Math.toDegrees(Math.acos(v));
 11     return k；
 12 }
 13 public double isSlope() {
 14     double k1=(this.y.getY() - this.z.getY())*(this.x.getX() - this.y.getX());
 15     double k2=(this.x.getY() - this.y.getY())*(this.y.getX() - this.z.getX());
 16     double k3=(this.z.getY() - this.a.getY())*(this.y.getX() - this.z.getX());
 17     double k4=(this.y.getY() - this.z.getY())*(this.z.getX() - this.a.getX());
 18     double k5=(this.a.getY() - this.b.getY())*(this.z.getX() - this.a.getX());
 19     double k6=(this.z.getY() - this.a.getY())*(this.a.getX() - this.b.getX());
 20     double k7=(this.b.getY() - this.x.getY())*(this.a.getX() - this.b.getX());
 21     double k8=(this.a.getY() - this.b.getY())*(this.b.getX() - this.x.getX());
 22     double k9=(this.x.getY() - this.y.getY())*(this.b.getX() - this.x.getX());
 23     double k10=(this.b.getY() - this.x.getY())*(this.x.getX() - this.y.getX());
 24     if(k1-k2==0||k3-k4==0||k5-k6==0||k7-k8==0||k9-k10==0)
 25     {
 26         return 1;
 27     }
 28     else {
 29         return 0;
 30     }
 31 }
 32 public boolean isParallelogram() {
 33     return true;
 34 }
 35 
 36 public double getArea() {
 37     double k1 = (this.x.getY() - this.y.getY())*(this.x.getY() - this.y.getY())+(this.x.getX() - this.y.getX())*(this.x.getX() - this.y.getX());
 38     double k2 = (this.y.getY() - this.z.getY())*(this.y.getY() - this.z.getY())+(this.y.getX() - this.z.getX())*(this.y.getX() - this.z.getX());
 39     double k3 = (this.z.getY() - this.a.getY())*(this.z.getY() - this.a.getY())+(this.z.getX() - this.a.getX())*(this.z.getX() - this.a.getX());
 40     double k4 = (this.a.getY() - this.b.getY())*(this.a.getY() - this.b.getY())+(this.a.getX() - this.b.getX())*(this.a.getX() - this.b.getX());
 41     double k5 = (this.b.getY() - this.x.getY())*(this.b.getY() - this.x.getY())+(this.b.getX() - this.x.getX())*(this.b.getX() - this.x.getX());
 42     double k6 = (this.x.getY() - this.z.getY())*(this.x.getY() - this.z.getY())+(this.x.getX() - this.z.getX())*(this.x.getX() - this.z.getX());
 43     double k7 = (this.x.getY() - this.a.getY())*(this.x.getY() - this.a.getY())+(this.x.getX() - this.a.getX())*(this.x.getX() - this.a.getX());
 44     double d1 = Math.sqrt(k1);
 45     double d2 = Math.sqrt(k2);
 46     double d3 = Math.sqrt(k3);
 47     double d4 = Math.sqrt(k4);
 48     double d5 = Math.sqrt(k5);
 49     double d6 = Math.sqrt(k6);
 50     double d7 = Math.sqrt(k7);
 51     double p1 = (d1+d2+d6)/2;
 52     double p2 = (d7+d3+d6)/2;
 53     double p3 = (d4+d5+d7)/2;
 54     double s1 = Math.sqrt(p1*(p1-d1)*(p1-d2)*(p1-d6));
 55     double s2 = Math.sqrt(p2*(p2-d7)*(p2-d3)*(p2-d6));
 56     double s3 = Math.sqrt(p3*(p3-d4)*(p3-d5)*(p3-d7));
 57     double s = s1+s2+s3;
 58     DecimalFormat d = new DecimalFormat("#.000");
 59     Double output = Double.valueOf(d.format(s));
 60     return output;
 61 }
 62 
 63 public double getPerimeter() {
 64     double k1 = (this.x.getY() - this.y.getY())*(this.x.getY() - this.y.getY())+(this.x.getX() - this.y.getX())*(this.x.getX() - this.y.getX());
 65     double k2 = (this.y.getY() - this.z.getY())*(this.y.getY() - this.z.getY())+(this.y.getX() - this.z.getX())*(this.y.getX() - this.z.getX());
 66     double k3 = (this.z.getY() - this.a.getY())*(this.z.getY() - this.a.getY())+(this.z.getX() - this.a.getX())*(this.z.getX() - this.a.getX());
 67     double k4 = (this.a.getY() - this.b.getY())*(this.a.getY() - this.b.getY())+(this.a.getX() - this.b.getX())*(this.a.getX() - this.b.getX());
 68     double k5 = (this.b.getY() - this.x.getY())*(this.b.getY() - this.x.getY())+(this.b.getX() - this.x.getX())*(this.b.getX() - this.x.getX());
 69     double k = Math.sqrt(k1)+Math.sqrt(k2)+Math.sqrt(k3)+Math.sqrt(k4)+Math.sqrt(k5);
 70     DecimalFormat d = new DecimalFormat("#.000");
 71     Double output = Double.valueOf(d.format(k));
 72     return output;
 73 }
 74 public boolean isLozenge() {
 75     double k1 = (this.x.getY() - this.y.getY())*(this.x.getY() - this.y.getY())+(this.x.getX() - this.y.getX())*(this.x.getX() - this.y.getX());
 76     double k2 = (this.y.getY() - this.z.getY())*(this.y.getY() - this.z.getY())+(this.y.getX() - this.z.getX())*(this.y.getX() - this.z.getX());
 77     double k3 = (this.z.getY() - this.a.getY())*(this.z.getY() - this.a.getY())+(this.z.getX() - this.a.getX())*(this.z.getX() - this.a.getX());
 78     double k4 = (this.a.getY() - this.x.getY())*(this.a.getY() - this.x.getY())+(this.a.getX() - this.x.getX())*(this.a.getX() - this.x.getX());
 79     if(k1==k2&&k2==k3&&k3==k4) {
 80         return true;
 81     }
 82     else
 83     {
 84         return false;
 85     }
 86 }
 87 
 88