樹結構

1.1 樹的定義

樹(Tree)：個節點構成的有限集合。當n = 0時，稱為空樹。對於任一棵非空樹(n>0)，它具備以下性質：

樹中有一個稱為"根(Root)"的特殊節點，用r表示；其餘節點可分為m(m>0)個互不相交的有限集、，...,，其中每個集合本身又是一棵樹，稱為原來樹的子樹(SubTree)。如下圖：

1.2 樹結構的術語

樹結構中有很多概念術語，在深入討論樹結構之前，我們先來介紹下跟樹結構有關的術語。為了方便理解記憶，結合具體的一棵樹結構來進行介紹，樹結構如下：

節點：樹中存儲的項。上圖中的A-L都是節點。

根節點：樹中最頂端的節點。在樹結構中只有它沒有父節點。上圖中的A為根節點。

節點的度：一個節點含有的子樹的個數。根節點A的度為3；子節點C的度為1。

樹的度：樹中最大節點度。樹中最大節點度為3(根節點A和子節點B的度均為3)，所以樹的度為3。

子節點(孩子節點)：緊鄰一個給定的節點之下，並且直接與給定節點相連的一個節點。一個節點可以有多個子節點。上圖中B-L都是子節點。

父節點(雙親節點)：緊鄰一個給定節點之上，且直接與給定節點相連的一個節點。一個節點只能有一個父節點。上圖中A、B、C、D、H都是父節點。

兄弟節點：擁有共同父節點的子節點。上圖中B、C、D是兄弟節點，E、F、G也是兄弟節點。

葉子節點：沒有子節點的節點。或者說度為0的節點。上圖中標綠的幾個節點都是葉子節點。

內部節點：至少有一個子節點的節點。B、C、D、H都是內部節點。

邊/分支：將一個父節點連接到其子節點的線。上圖中的線就是邊也稱為分支。

後代(子孫)：以某節點為根的子樹中任一節點都稱為該節點的後代。E、F、G是節點B的後代；H、K、L是節點C的後代，B-L的所有節點都是根節點A的後代。

祖先：從根到該節點所經分支上的所有節點。節點D是I、J的祖先；根節點A是所有節點的祖先。

路徑：連接一個節點與其後代節點邊的序列。A-B-E和A-C-H-K都可以稱作一條路徑。

路徑長度：路徑中邊的數目。路徑A-B-E的路徑長度為2；路徑A-C-H-K的路徑長度為3。

節點的層次：從根節點定義，根節點為第1層，根節點的子節點為第2層，依次類推。節點的層在上圖中已經標出。

深度(高度)：葉子節點所在的最大層次。上圖中樹的深度為4。

森林：m棵不相交的樹的集合。分別以B、C、D為根節點的子樹組成的集合可以看做一個森林。

以上就是樹結構的一些術語。

1.3 樹的分類

樹結構可以分為兩大類：有序樹和無序樹。樹中任意節點間沒有順序關係，那麼稱其為無序樹，也稱自由樹。相對的，樹中的任意節點有順序關係，稱其為有序樹。在有序樹中，子節點被視為按照從左到右的順序排列，最左邊的子節點稱為第一個子節點，最右邊的子節點稱為最後一個子節點。我們研究的最多的樹結構就是有序樹。而有序樹中最具代表性的樹結構就是二叉樹。

二叉樹就是度不超過2的有序樹結構。 二叉樹中的每個節點最多只能有兩個分支，分別稱為左子樹和右子樹。

根據二叉樹的定義，會有如下兩種極端的二叉樹：

​

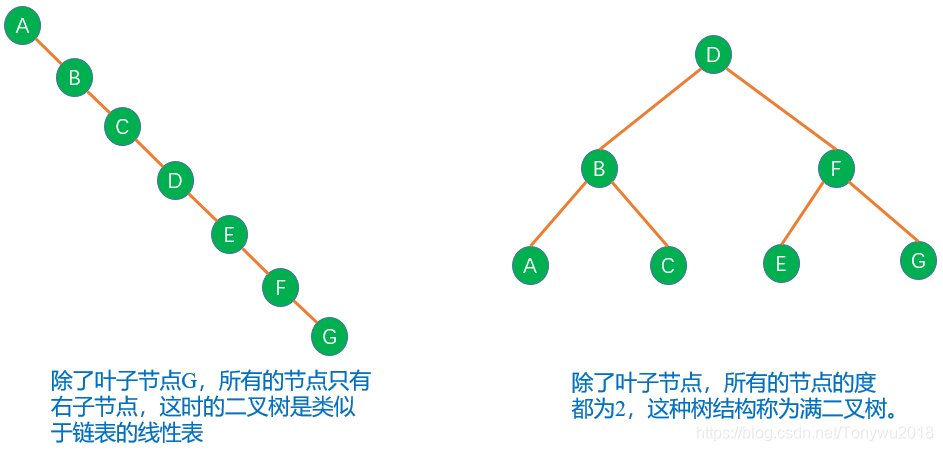
根據二叉樹的形狀，有以下幾種常見的二叉樹：

平衡二叉樹：當且僅當任意節點的兩棵子樹的高度差不大於1的二叉樹。

完全二叉樹：除了最後一層外，其他層的節點數目都達到最大的二叉樹。完全二叉樹是平衡二叉樹的一個特例，完全二叉樹最後一層上的節點都是從左到右填充的。對於一顆k層的完全二叉樹，其節點總數最少的情況是：最後一層只有一個節點，此時節點數目為：；其節點總數最多的情況是：最後一層節點數目達到最大，即滿二叉樹，此時節點數目為：。對於節點數目為k的完全二叉樹，其深度為：

滿二叉樹：所有層的節點數目均達到最大的二叉樹。滿二叉樹是完全二叉樹的一個特例。對於深度為k的滿二叉樹，其節點數目是：；對於節點數目為k的滿二叉樹，其深度為：。

幾種二叉樹的結構圖如下：

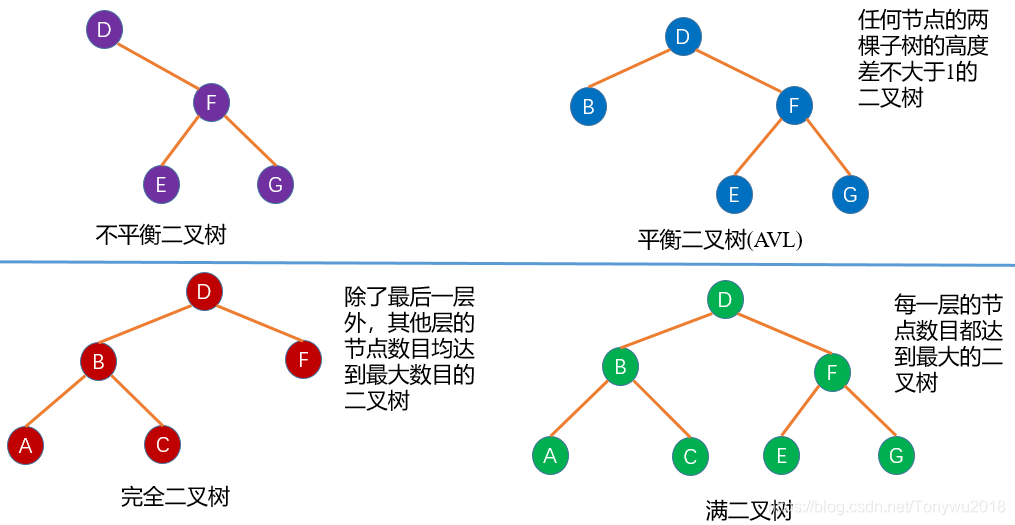
關於二叉樹還有一個性質：二叉樹中葉子節點數為(因為葉子節點的度為0，所以下標為0)，度為2的節點數為 ，那麼有: n₀ = n₂ + 1

解析：關於上面等式關係的求解我們可以這樣考慮。假設二叉樹的總節點數為，因為二叉樹的節點度只有0、1、2三種情況，假設節點度為0、1、2的節點數分別為：n₀、n₁和n₂。那麼有n = n₀ + n₁ + n₂。二叉樹中節點度為1的節點有1條邊連接到其子節點、節點度為2的節點有2條邊連接到其子節點，假設二叉樹有E條邊，那麼E = n₁ + 2n₂。而我們知道，在二叉樹中節點總數和邊的數目有這樣的關係：n = E +1 = n₁ + 2n₂ + 1。聯立加粗的兩個等式，容易得出 n₀ = n₂ + 1。