LRU:最近最少使用緩存 LRU是Least Recently Used的縮寫,即最近最少使用,是一種常用的頁面置換演算法,選擇最近最久未使用的頁面予以淘汰。該演算法賦予每個頁面一個訪問欄位,用來記錄一個頁面自上次被訪問以來所經歷的時間 t,當須淘汰一個頁面時,選擇現有頁面中其 t 值最大的,即最近最少 ...
LRU:最近最少使用緩存
LRU是Least Recently Used的縮寫,即最近最少使用,是一種常用的頁面置換演算法,選擇最近最久未使用的頁面予以淘汰。該演算法賦予每個頁面一個訪問欄位,用來記錄一個頁面自上次被訪問以來所經歷的時間 t,當須淘汰一個頁面時,選擇現有頁面中其 t 值最大的,即最近最少使用的頁面予以淘汰。(引自百度百科)
運用所掌握的數據結構,設計和實現一個 LRU (Least Recently Used,最近最少使用) 緩存機制 。
實現
LRUCache類:
LRUCache(int capacity)以正整數作為容量capacity初始化 LRU 緩存int get(int key)如果關鍵字key存在於緩存中,則返回關鍵字的值,否則返回-1。void put(int key, int value)如果關鍵字已經存在,則變更其數據值;如果關鍵字不存在,則插入該組「關鍵字-值」。當緩存容量達到上限時,它應該在寫入新數據之前刪除最久未使用的數據值,從而為新的數據值留出空間。
解題思路
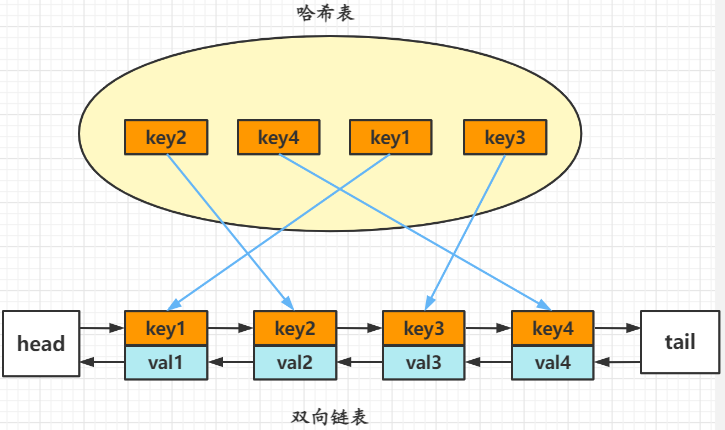
LRU緩存機制對應的結構其實就是一個雙向鏈表,由於get和put方法必須是\(O(1)\)的時間複雜度,可以使用一個哈希表快速定位,找出緩存項在雙向鏈表中的位置,隨後將其移動到雙向鏈表的頭部(最近使用的排在隊頭,最久未使用的排在隊尾),即可在 \(O(1)\) 的時間內完成 get 或者 put 操作。
因此,LRU 演算法的核心數據結構就是哈希鏈表,即雙向鏈表和哈希表的結合體。
對於get操作,首先在哈希map中判斷key是否存在:
- 如果key不存在,直接返回-1;
- 如果key存在,則
key對應的節點就是最近被使用的節點。通過哈希表定位到該節點在雙向鏈表中的位置,並將其移動到雙向鏈表的頭部,最後返回該節點的值。
對於put操作,首先也要在哈希 map 中判斷 key 是否存在:
- 如果
key不存在,使用key和value創建一個新的節點,在雙向鏈表的頭部添加該節點,並將key和該節點添加進哈希表中。然後判斷雙向鏈表是否滿了,如果超出了容量,則刪除雙向鏈表的尾部節點(把最久未使用的尾部結點給刪了,給新節點騰地兒),並刪除哈希表中對應的鍵值。最後把新加入的key添加到雙向鏈表的頭部和哈希表中; - 如果
key存在,則與get操作類似,通過查詢哈希表得到key在雙向鏈表的位置,刪除該結點。最後把新加入的key添加到雙向鏈表的頭部和哈希表中;
在雙向鏈表初始化時,使用一個啞元頭部(dummy head)和啞元尾部(dummy tail)標記占位,這樣在添加節點和刪除節點的時候就不需要檢查相鄰的節點是否存在,防止空指針。
代碼實現
自定義雙向鏈表結構(面試推薦✔)
class LRUCache {
// 自定義結點類型
static class Node {
private int key, val;
private Node next, prev;
public Node(int k, int v) {
this.key = k;
this.val = v;
}
}
// 自定義雙向鏈表
static class DoubleList {
private Node head, tail;
// 構造雙向鏈表(head和tail是啞元結點,占位用的)
public DoubleList() {
this.head = new Node(-1, -1);
this.tail = new Node(-1, -1);
head.next = tail;
tail.prev = head;
}
// 在鏈表頭部添加結點(頭插法)
public void addFirst(Node node) {
node.prev = head;
node.next = head.next;
head.next.prev = node;
head.next = node;
}
// 刪除指定結點Node
public void remove(Node node) {
node.prev.next = node.next;
node.next.prev = node.prev;
}
// 刪除鏈表尾節點,並返回該結點
public Node removeLast() {
Node node = tail.prev;
remove(node);
return node;
}
}
private HashMap<Integer, Node> map; // 輔助map
private DoubleList cache;
private int cap; // 雙向鏈表的最大容量
public LRUCache(int capacity) {
map = new HashMap<>();
cache = new DoubleList();
this.cap = capacity;
}
public int get(int key) {
if(! map.containsKey(key)) return -1; // map中不存在key,get不到了
Node node = map.get(key);
cache.remove(node);
cache.addFirst(node);
return node.val;
}
public void put(int key, int value) {
// 要添加的結點封裝成一個node
Node node = new Node(key, value);
if(map.containsKey(key)) {
cache.remove(map.get(key)); // 已經有這個key了,舊值刪了,新值頭部添加操作在底下
} else if(map.size() >= cap) {
// 雙端鏈表滿了,則把最久未使用的尾部結點給刪了,給新節點騰地兒
Node lastNode = cache.removeLast();
map.remove(lastNode.key);
}
// 鏈表和map同步添加
cache.addFirst(node);
map.put(key, node);
}
// 測試
public static void main(String[] args) {
LRUCache lruCache = new LRUCache(2); // 初始化雙向鏈表和map
lruCache.put(1, 1);
lruCache.put(2, 2);
lruCache.get(1);
lruCache.put(3, 3);
lruCache.get(2);
System.out.println(lruCache.map);
}
}
在 Java 語言中,同樣有類似的數據結構 LinkedHashMap,內部已經封裝好添加查詢的方法。但是面試時不推薦使用,還是推薦使用上面這種方式。
class LRUCache {
private int cap;
private LinkedHashMap<Integer, Integer> cache;
public LRUCache(int capacity) {
this.cap = capacity;
this.cache = new LinkedHashMap<>()
}
// 使用了key,就得設這個key為最近使用
public int get(int key) {
if(! cache.containsKey(key)) {
return -1;
}
makeRecently(key);
return cache.get(key);
}
public void put(int key, int value) {
// key 存在於鏈表中
if(cache.containsKey(key)) {
cache.put(key, value); // 修改 key 的值
makeRecently(key); // 將 key 變為最近使用
return;
}
// 插入元素前需要判斷鏈表容量是否已滿,淘汰最久未使用的key
if(cache.size() >= this.cap) {
// 鏈表頭部就是最久未使用的 key
int oldestKey = cache.keySet().iterator().next();
cache.remove(oldestKey);
}
// 將新的 key 添加鏈表尾部
cache.put(key, value);
}
// 設置key為最近使用,key先刪了移到鏈表尾
private void makeRecently(int key) {
int val = cache.get(key);
// 刪除 key,重新插入到隊尾
cache.remove(key);
cache.put(key, val);
}
// 測試
public static void main(String[] args) {
LRUCache lruCache = new LRUCache(2);
lruCache.put(1,1);
lruCache.put(2,2);
lruCache.get(1);
lruCache.put(3,3);
lruCache.get(2);
System.out.println(cache);
}
}
複雜度
- 時間複雜度:put 和 get 操作的平均時間複雜度都為\(O(1)\);
- 空間複雜度:\(O(capacity)\),哈希表和雙向鏈表中最多存儲
capacity個元素。



