本文講解了SVM的原理,以及代碼中用到的公式手寫的推導的過程,以及對應的SVM簡單代碼的實現及詳解,還有加入核函數解決非線性函數的的方法及代碼的詳解 ...
1.支持向量機簡介
-
英文名為Support Vector Machine簡稱為SVM,是一種二分類模型
-
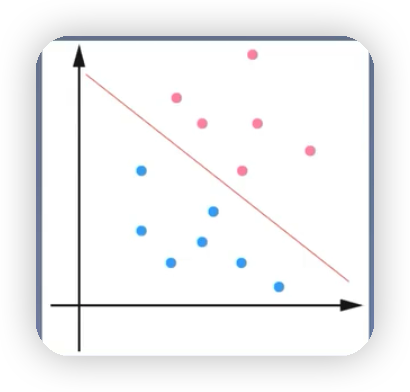
線性可分支持向量機:如下圖就可以通過一條紅色的直線將藍色的球和紅色的球完全區分開,該直線被稱為線性分類器,如果是高維的,就可以通過一個超平面將三維立體空間里的樣本點給分開。通過硬間隔最大化,學習一個線性分類器。
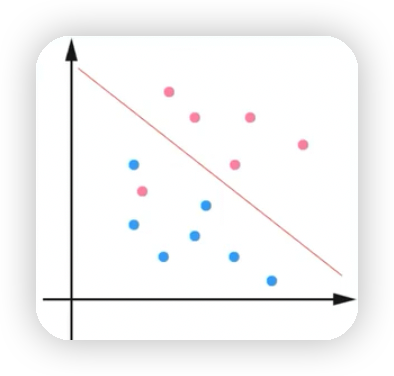
- 線性支持向量機:如下圖有一個紅色的點無論怎麼分,都無法將藍點的點和紅色的點完全區分開,但是這種情況下絕大多數的點都可以通過該直線分割開來,也就是通過軟間隔最大化,學習一個線性分類器
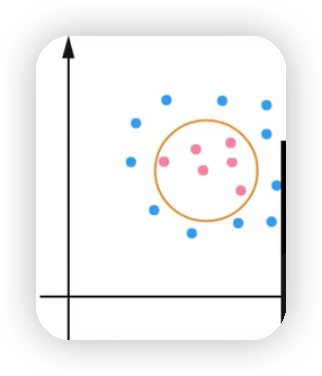
- 非線性支持向量機:如下圖將藍色的點和紅色的點區分開的是一個圈並不是通過直線來區分開。也就是通過核技巧,學習一個非線性分類器
- 支持向量:就是支持或支撐平面(間隔平面)上把兩類類別劃分開來的超平面的向量點,如下圖樣本點過間隔平面的這些點被稱為向量點,這些點組成的向量為支持向量。

2.線性可分支持向量機
如下圖,要找到離黑色實線最近的樣本點,使得該點到黑線的距離達到最大,該距離可以用我們以前學過的點到直線的距離公式來求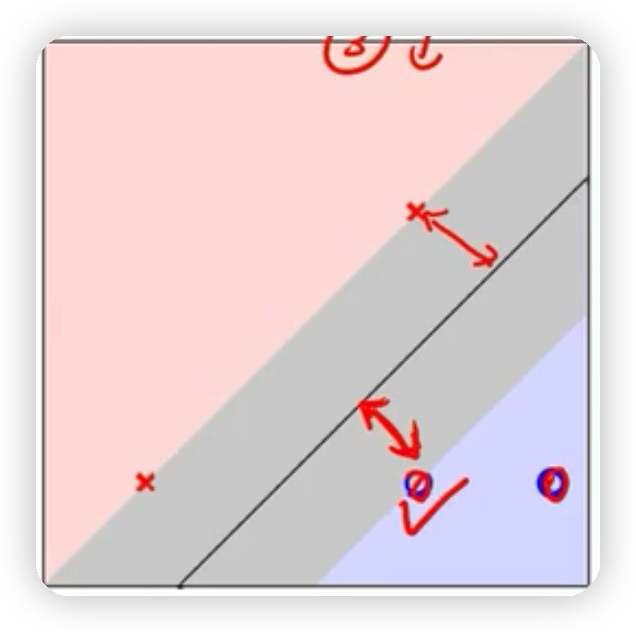
-
幾何間隔
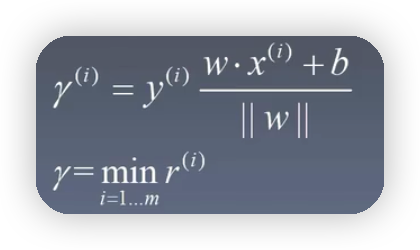
以上公式的來源:假如有一個點(A,B)到直線方程為ax+by+c=0的距離如下圖所示
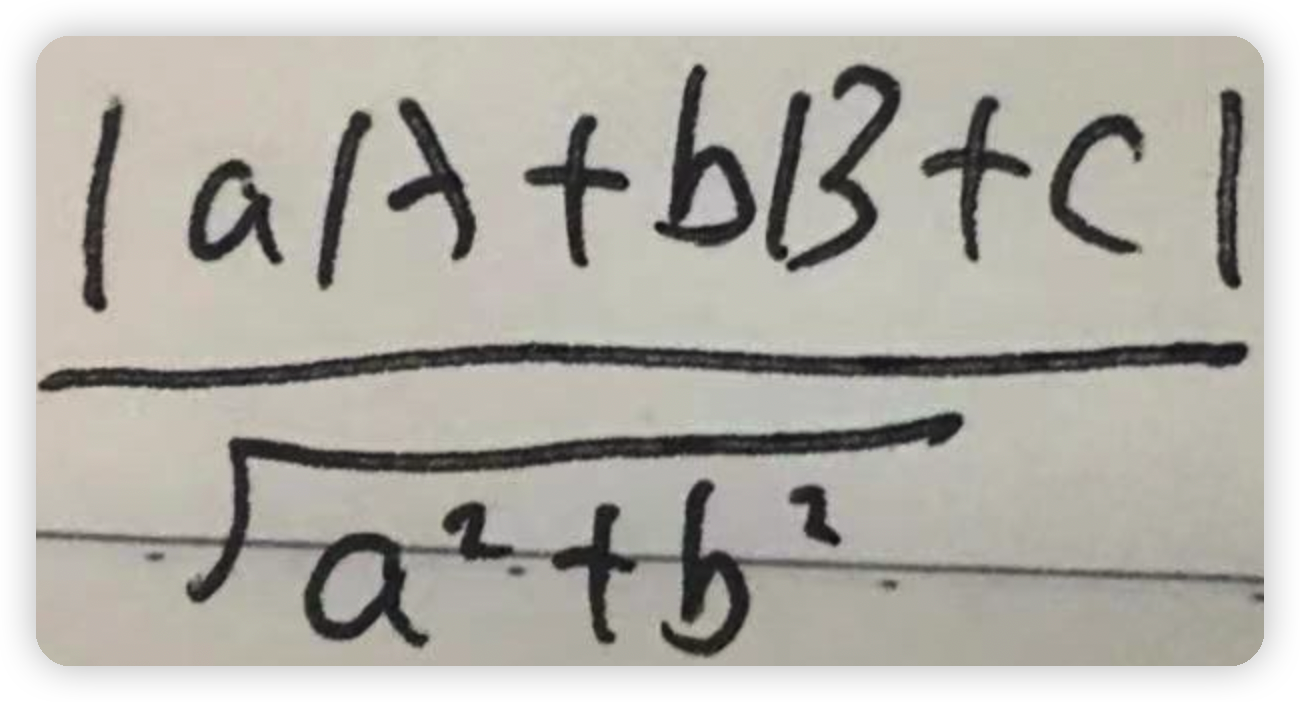
如果將直線方程改為w0x0+w1x1+b=0,那麼點到直線的距離就可以改為如下圖所示
再進一步化簡即可得到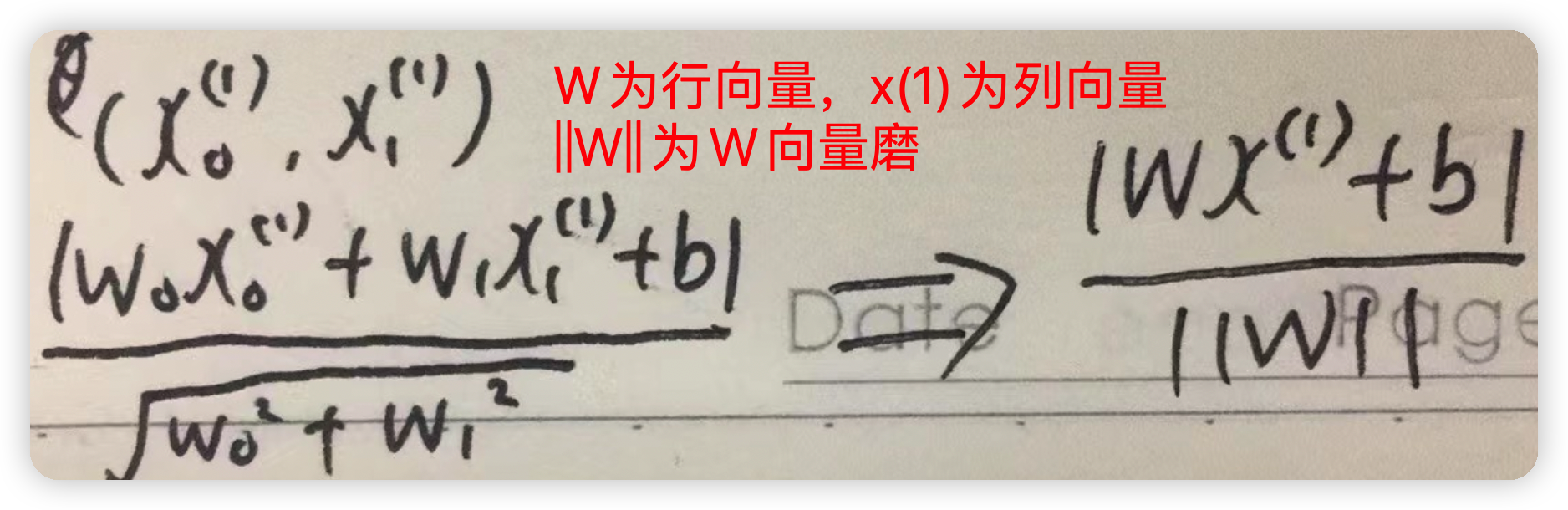
如果當前的樣本點屬於正樣本點,則其y的值為1,反之y的值為-1,所以為了去掉距離公式中的絕對值,可以再前面乘以個y的值,因為如果為負樣本,距離值為負,y的值也是負,這樣得到的乘積也依然為正,和以前沒有乘以y,然後加絕對值得到的結果一致由以上步驟就可以得到幾何間隔的公式
-
函數間隔
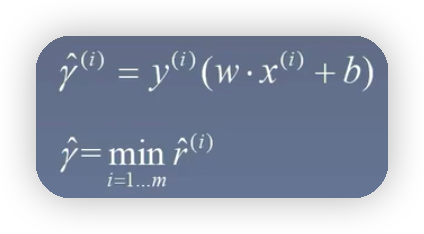
與幾何間隔相比較一個最大的區別就是沒有了分母的||W||,這樣的話,就可以通過縮放方程的繫數來更改函數間隔的值,同樣也就可以通過縮放繫數值,來使得函數間隔的值設置為1,舉個簡單的例子假設直線方程為2x+y+1=0,樣本點的坐標為(1,2),則不難算出集合間隔點到直線的距離為5/根號5,而函數間隔為5;如果將直線方程的繫數擴大2倍,也就是變為4x+2*y+2=0,此時算出來的幾何間隔的值任然不變,但是函數間隔的值變為10,也就是說通過縮放方程繫數的值,可以改變函數間隔的值,而不能改變幾何間隔的值 -
兩者的關係


最大間隔分離超平面

3.SVM目標函數的求解
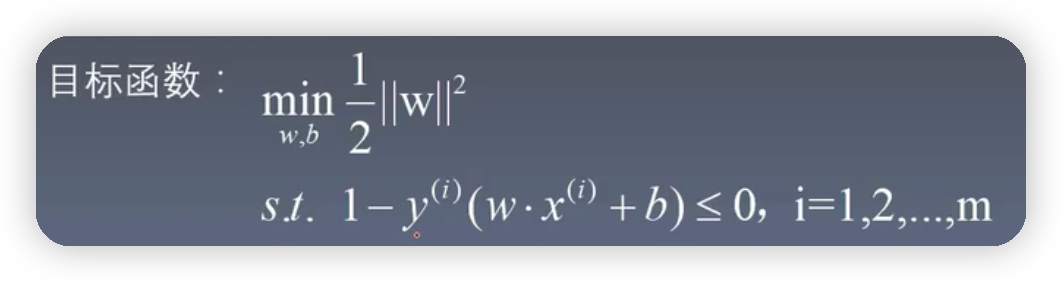
由目標函數構造拉格朗日函數,下圖的變數寫錯了應該是L(w,b,a)

然後對拉格朗日求解

3.1對alpha求最大值

3.2舉例求解

求解步驟如下圖:

4.線性支持向量機
4.1概念
有些樣本點無論怎麼分,都不能用一條直線將樣本點完全分開,但是對於絕大多數樣本點還是可以通過超平面給分隔開。
4.2目標函數的優化


由上圖可知得到的結果與線性可分向量機得到的結果可以說是完全一樣,唯一的區別就是約束條件不太一樣

5.非線性支持向量機
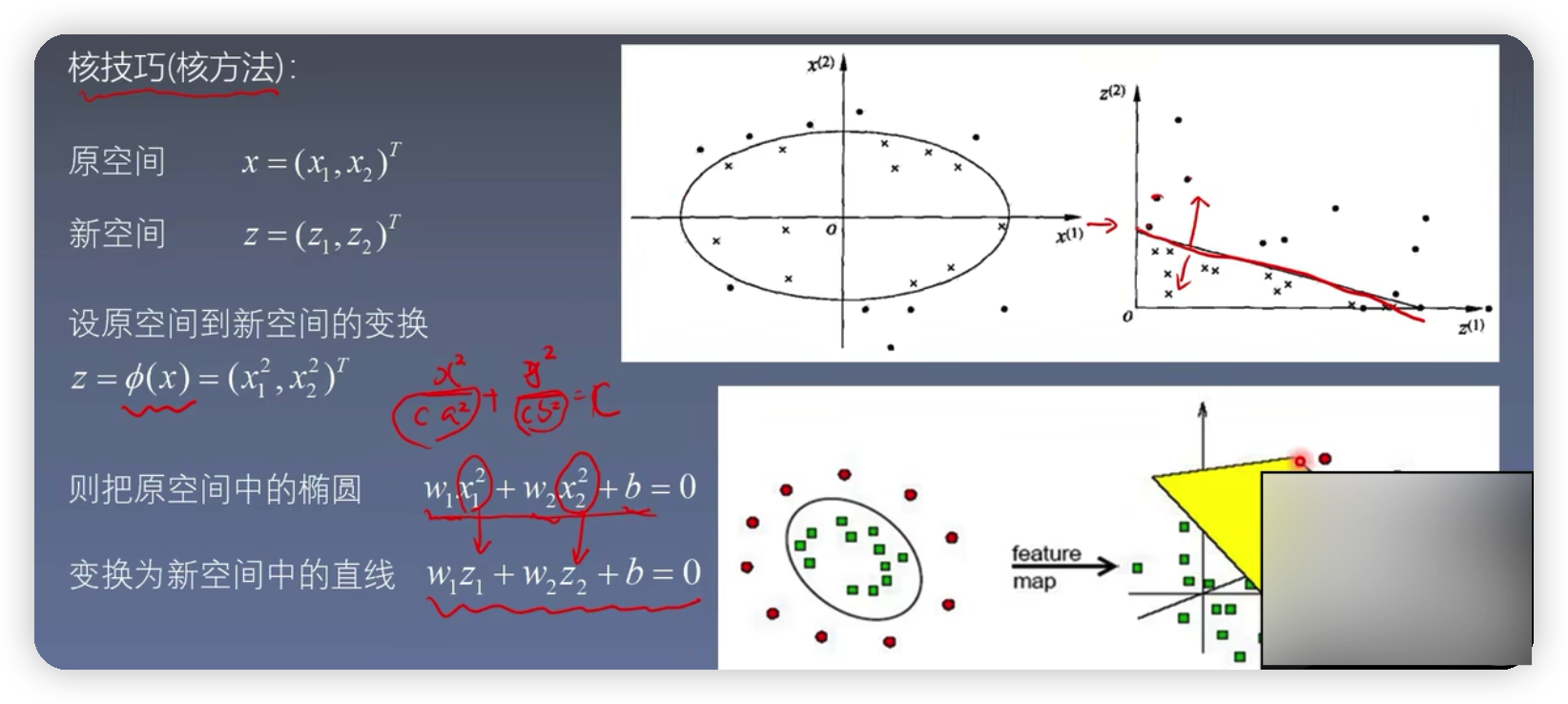
由上圖可知在原空間中,用一個橢圓曲線將圓點和xx分開,總所周知,橢圓的方程為x^2 / a^2 + y^2 / b^2,為了使得其與機器學習相關,可以再左右添加一個參數c,然後用w1表示1/c* a^2 , w2表示1 / c*b^2, b表示-c,則橢圓方程可以簡化為w1 * x1^2 + w2 * x2^2 + b=0,坐在新空間中存在一種對應關係,使得z1= x1^2 ,z2= x2^2 ,則橢圓方程可以進一步簡化為w1 * Z1+ w2 * Z2+b=0,這個過程也被稱為核技巧,也就是將元空間的曲線方程,轉化為新空間的線性可分的直線方程
由下圖可知,當o(x)取不同維數的函數,經過映射之後得到的核函數都是一樣的。所以核函數的原理就是通過在低維空間的計算,而去完成在高維空間所能完成的事情


5.SMO演算法推導結果
如果不知道推導的過程其實也不影響後面的學習,知道每個公式在代碼裡面怎麼用就可以了
5.1SMO演算法簡易版代碼實現
from numpy import *
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.patches import Circle
def loadDataSet(fileName):
dataMat=[];labelMat=[]#數據集以及標簽集分開存儲
fr=open(fileName)
for line in fr.readlines():#讀取文件的每一行數據
lineArr=line.strip().split('\t')#每個數據以空格分開
dataMat.append([float(lineArr[0]),float(lineArr[1])])#將每一行的第一個數據和第二個數據存放在數據集中
labelMat.append(float(lineArr[2]))#每一行的第三個數據存放在標簽集中
return dataMat,labelMat
#alpha的選取,隨機選擇一個不等於i值得j
def selectJrand(i,m):#i的值就是當前選定的alpha的值
j=i
while(j==i):
j=int(random.uniform(0,m))
return j
#進行剪輯
def clipAlpha(aj,H,L):
if aj>H:
aj=H
if L>aj:
aj=L
return aj
#dataMatIn就是之前講的公式里的x,classLabels就是之前公式里的y
#toler誤差值達到多少時可以停止,maxIter迭代次數達到多少是可以停止
def smoSimple(dataMatIn,classLabels,C,toler,maxIter):
dataMatrix=mat(dataMatIn);labelMat=mat(classLabels).transpose()
#初始化b為0
b=0
#獲取數據維度
m,n=shape(dataMatrix)
#初始化所有alpha為0
alphas=mat(zeros((m,1)))
iter=0
#迭代求解
while(iter<maxIter):
alphaPairsChanged=0
for i in range(m):
#計算g(xi)
gXi= float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T))+b
#計算Ei
Ei=gXi-float(labelMat[i])
if((labelMat[i]*Ei<-toler) and (alphas[i]<C)) or ((labelMat[i]*Ei>toler) and (alphas[i]>0)):
#隨機選擇一個待優化的alpha(先隨機出alpha下標)
j=selectJrand(i,m)
#計算g(xj)
gXj = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[j, :].T)) + b
#計算Ej
Ej = gXj - float(labelMat[j])
#把原來的惡alpha的值複製一份,作為old的值
alphaIold=alphas[i].copy();alpaJold=alphas[j].copy()
#計算上下界
if(labelMat[i]!=labelMat[j]):
L=max(0,alphas[j]-alphas[i])
H=min(C,C+alphas[j]-alphas[i])
else:
L=max(0,alphas[j]+alphas[i]-C)
H=min(C,alphas[j]-alphas[i])
if L==H:
print("L==H")
continue
#計算eta:在公式里就是計算K11+K22-2K12,但是這裡算的負的eta
eta=2*dataMatrix[i,:]*dataMatrix[j,:].T-dataMatrix[i,:]*dataMatrix[i,:].T-dataMatrix[j,:]*dataMatrix[j,:].T
if eta>=0:
print("eta>=0")
continue
#計算alpha[j],為了和公式對應把j看出2
alphas[j]-=labelMat[j]*(Ei-Ej)/eta
#剪輯alphas[j],為了和公式對應把j看成2
alphas[j]=clipAlpha(alphas[j],H,L)
if(abs(alphas[j]-alpaJold)<0.00001):
print("j not moving enough")
continue
#計算alphas[i],為了和公式對應把i看成1
alphas[i] += labelMat[i]*labelMat[j]*(alpaJold-alphas[j])
#計算b1
b1=-Ei-labelMat[i]*(dataMatrix[i,:]*dataMatrix[i,:].T)*(alphas[i]-alphaIold)-labelMat[j]*(dataMatrix[j,:]*dataMatrix[i,:].T)*(alphas[j]-alpaJold)+b
#計算b2
b2=-Ej-labelMat[i]*(dataMatrix[i,:]*dataMatrix[j,:].T)*(alphas[i]-alphaIold)-labelMat[j]*(dataMatrix[j,:]*dataMatrix[j,:].T)*(alphas[j]-alpaJold)+b
#求解b
if(0<alphas[i]) and (C>alphas[j]):
b = b1
elif (0<alphas[j]) and (C>alphas[j]):
b = b2
else:
b=(b1+b2)/2.0
alphaPairsChanged+=1
print("iter:%d i:%d,pairs changed %d" %(iter,i,alphaPairsChanged))
if(alphaPairsChanged==0):
iter+=1
else:
iter=0
print("iteration number:%d" %iter)
return b,alphas
#計算w的值
def calcWs(dataMat, labelMat, alphas):
X=mat(dataMat);labelMat=mat(labelMat).transpose()
m,n=shape(X)
#初始化w都為1
w=zeros((n,1))
#迴圈計算
for i in range(m):
w+=multiply(alphas[i]*labelMat[i],X[i,:].T)
return w
#畫圖
def showClassifer(dataMat, labelMat, b,alphas,w):
fig=plt.figure()
ax=fig.add_subplot(111)
cm_dark=mpl.colors.ListedColormap(['g','r'])
ax.scatter(array(dataMat)[:,0],array(dataMat)[:,1],c=array(labelMat).squeeze(),cmap=cm_dark,s=30)
#畫決策平面
x=arange(-2.0,12.0,0.1)
y=(-w[0]*x-b)/w[1]
ax.plot(x,y.reshape(-1,1))
ax.axis([-2,12,-8,6])
#畫支持向量
alphas_non_zeros_index=where(alphas>0)
for i in alphas_non_zeros_index[0]:
circle= Circle((dataMat[i][0],dataMat[i][1]),0.2,facecolor='none',edgecolor=(0,0.8,0.8),linewidth=3,alpha=0.5)
ax.add_patch(circle)
plt.show()
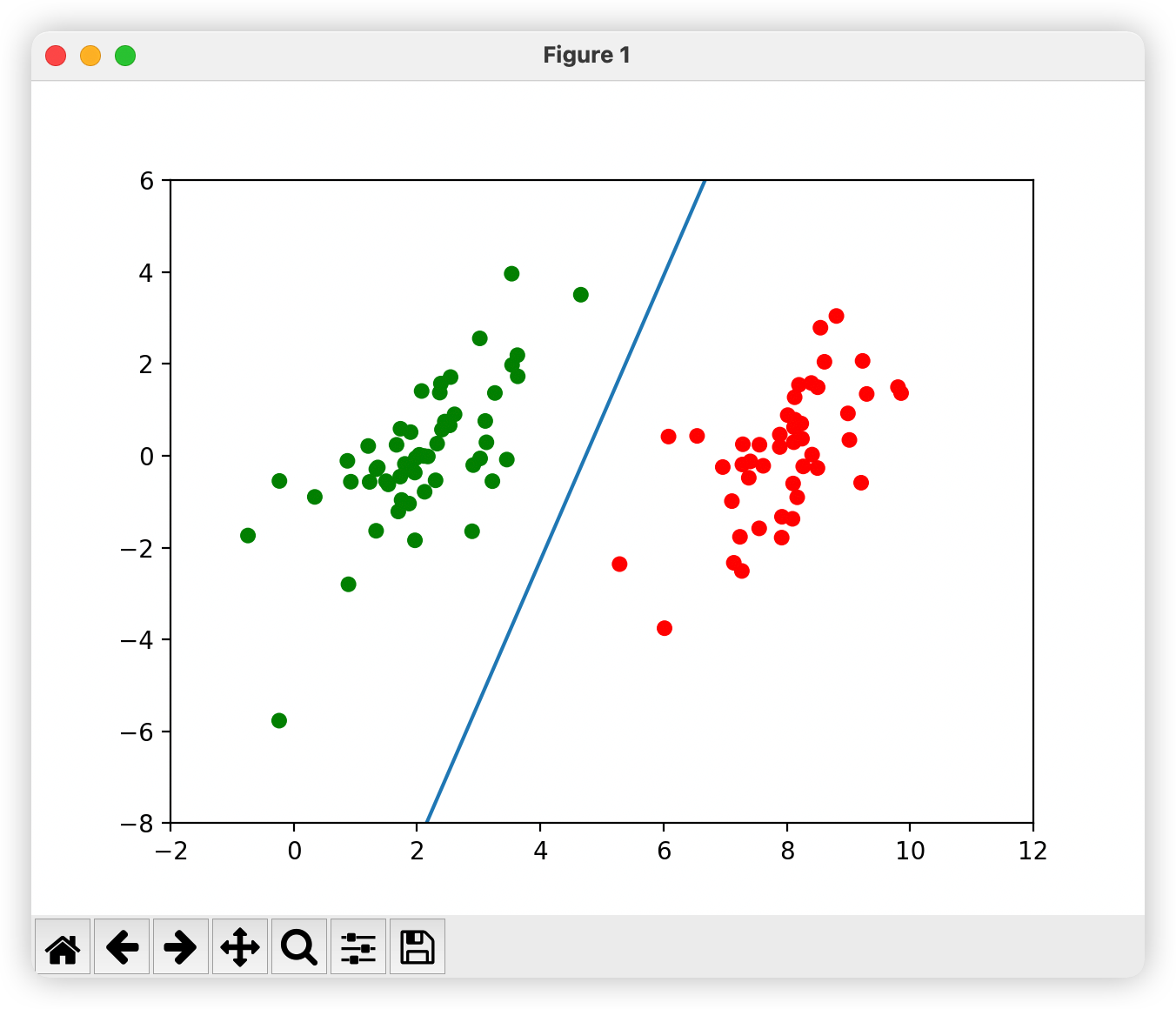
if __name__ == '__main__':
dataMat, labelMat = loadDataSet('testSet.txt')
b,alphas=smoSimple(dataMat,labelMat,0.6,0.001,40)
w = calcWs(dataMat, labelMat, alphas)
showClassifer(dataMat, labelMat, b,alphas,w)
畫決策平面
x=arange(-2.0,12.0,0.1)
y=(-w[0]*x-b)/w[1]
ax.plot(x,y.reshape(-1,1))
ax.axis([-2,12,-8,6])
plt.show()
畫支持向量
alphas_non_zeros_index=where(alphas>0)
for i in alphas_non_zeros_index[0]:
circle= Circle((dataMat[i][0],dataMat[i][1]),0.2,facecolor='none',edgecolor=(0,0.8,0.8),linewidth=3,alpha=0.5)
ax.add_patch(circle)
plt.show()

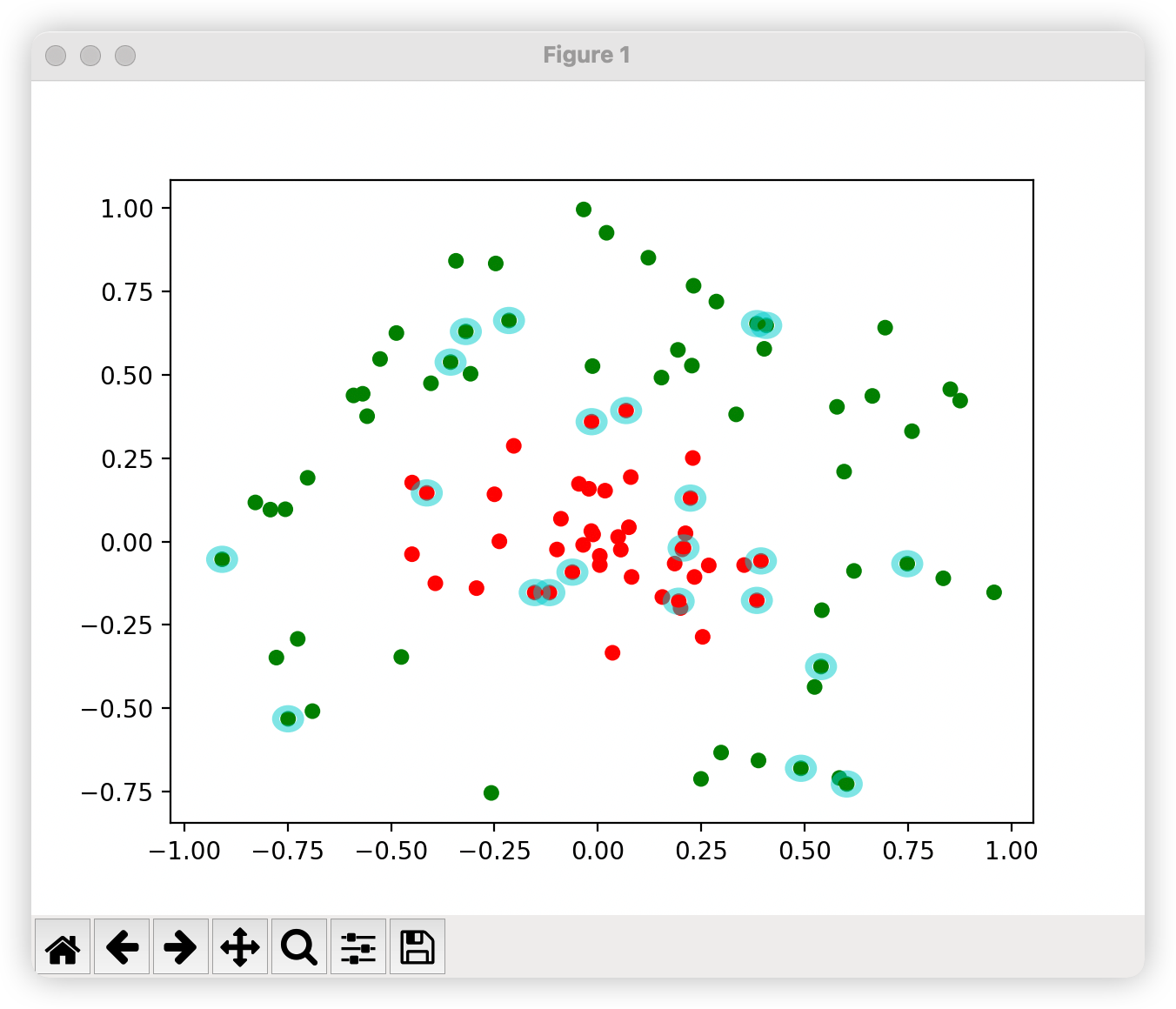
5.2引入核函數
from numpy import *
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.patches import Circle
class optStruct:
"""
數據結構,維護所有需要操作的值
Parameters:
dataMatIn - 數據矩陣
classLabels - 數據標簽
C - 鬆弛變數
toler - 容錯率
"""
def __init__(self, dataMatIn, classLabels, C, toler, kTup):
self.X = dataMatIn #數據矩陣
self.labelMat = classLabels #數據標簽
self.C = C #鬆弛變數
self.tol = toler #容錯率
self.m = shape(dataMatIn)[0] #數據矩陣行數
self.alphas = mat(zeros((self.m,1))) #根據矩陣行數初始化alpha參數為0
self.b = 0 #初始化b參數為0
self.eCache = mat(zeros((self.m,2))) #根據矩陣行數初始化虎誤差緩存,第一列為是否有效的標誌位,第二列為實際的誤差E的值。
self.K = mat(zeros((self.m, self.m))) # 初始化核K
for i in range(self.m): # 計算所有數據的核K
self.K[:, i] = kernelTrans(self.X, self.X[i, :], kTup)
def loadDataSet(fileName):
dataMat=[];labelMat=[]#數據集以及標簽集分開存儲
fr=open(fileName)
for line in fr.readlines():#讀取文件的每一行數據
lineArr=line.strip().split('\t')#每個數據以空格分開
dataMat.append([float(lineArr[0]),float(lineArr[1])])#將每一行的第一個數據和第二個數據存放在數據集中
labelMat.append(float(lineArr[2]))#每一行的第三個數據存放在標簽集中
return dataMat,labelMat
def calcEk(oS, k):
"""
計算誤差
Parameters:
oS - 數據結構
k - 標號為k的數據
Returns:
Ek - 標號為k的數據誤差
"""
fXk = float(multiply(oS.alphas, oS.labelMat).T * oS.K[:, k] + oS.b)
Ek = fXk - float(oS.labelMat[k])
return Ek
def selectJ(i, oS, Ei):
"""
內迴圈啟發方式2
Parameters:
i - 標號為i的數據的索引值
oS - 數據結構
Ei - 標號為i的數據誤差
Returns:
j, maxK - 標號為j或maxK的數據的索引值
Ej - 標號為j的數據誤差
"""
maxK = -1; maxDeltaE = 0; Ej = 0 #初始化
oS.eCache[i] = [1,Ei] #設為有效 #根據Ei更新誤差緩存
validEcacheList = nonzero(oS.eCache[:,0].A)[0] #返回誤差不為0的數據的索引值
if (len(validEcacheList)) > 1: #有不為0的誤差
for k in validEcacheList: #迭代所有有效的緩存,找到誤差最大的E
if k == i: continue #不計算i,浪費時間
Ek = calcEk(oS, k) #計算Ek
deltaE = abs(Ei - Ek) #計算|Ei-Ek|
if (deltaE > maxDeltaE): #找到maxDeltaE
maxK = k; maxDeltaE = deltaE; Ej = Ek
return maxK, Ej #返回maxK,Ej
else: #沒有不為0的誤差
j = selectJrand(i, oS.m) #隨機選擇alpha_j的索引值
Ej = calcEk(oS, j) #計算Ej
return j, Ej
#跟新緩存
def updateEk(oS, k):
"""
計算Ek,並更新誤差緩存
Parameters:
oS - 數據結構
k - 標號為k的數據的索引值
Returns:
無
"""
Ek = calcEk(oS, k) #計算Ek
oS.eCache[k] = [1,Ek] #更新誤差緩存
def innerL(i,oS):
"""
優化的SMO演算法
Parameters:
i - 標號為i的數據的索引值
oS - 數據結構
Returns:
1 - 有任意一對alpha值發生變化
0 - 沒有任意一對alpha值發生變化或變化太小
"""
# 步驟1:計算誤差Ei
Ei = calcEk(oS, i)
# 優化alpha,設定一定的容錯率。
if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or (
(oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
# 使用內迴圈啟發方式2選擇alpha_j,並計算Ej
j, Ej = selectJ(i, oS, Ei)
# 保存更新前的aplpha值,使用深拷貝
alphaIold = oS.alphas[i].copy()
alphaJold = oS.alphas[j].copy()
# 步驟2:計算上下界L和H
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L == H:
print("L==H")
return 0
# 步驟3:計算eta
eta = 2.0 * oS.K[i, j] - oS.K[i, i] - oS.K[j, j]
if eta >= 0:
print("eta>=0")
return 0
# 步驟4:更新alpha_j
oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta
# 步驟5:修剪alpha_j
oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
# 更新Ej至誤差緩存
updateEk(oS, j)
if (abs(oS.alphas[j] - alphaJold) < 0.00001):
print("alpha_j變化太小")
return 0
# 步驟6:更新alpha_i
oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j])
# 更新Ei至誤差緩存
updateEk(oS, i)
# 步驟7:更新b_1和b_2
b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, i] - oS.labelMat[j] * (
oS.alphas[j] - alphaJold) * oS.K[i, j]
b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, j] - oS.labelMat[j] * (
oS.alphas[j] - alphaJold) * oS.K[j, j]
# 步驟8:根據b_1和b_2更新b
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]):
oS.b = b2
else:
oS.b = (b1 + b2) / 2.0
return 1
else:
return 0
#alpha的選取,隨機選擇一個不等於i值得j
def selectJrand(i,m):#i的值就是當前選定的alpha的值
j=i
while(j==i):
j=int(random.uniform(0,m))
return j
#進行剪輯
# aj - alpha值
# H - alpha上限
# L - alpha下限
def clipAlpha(aj,H,L):
if aj>H:
aj=H
if L>aj:
aj=L
return aj
#dataMatIn就是之前講的公式里的x,classLabels就是之前公式里的y
#toler誤差值達到多少時可以停止,maxIter迭代次數達到多少是可以停止
def smoSimple(dataMatIn,classLabels,C,toler,maxIter,kTup = ('lin',0)):
"""
完整的線性SMO演算法
Parameters:
dataMatIn - 數據矩陣
classLabels - 數據標簽
C - 鬆弛變數
toler - 容錯率
maxIter - 最大迭代次數
kTup - 包含核函數信息的元組
Returns:
oS.b - SMO演算法計算的b
oS.alphas - SMO演算法計算的alphas
"""
oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler, kTup) #初始化數據結構iter = 0 # 初始化當前迭代次數
iter=0
entireSet = True
alphaPairsChanged = 0
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)): # 遍歷整個數據集都alpha也沒有更新或者超過最大迭代次數,則退出迴圈
alphaPairsChanged = 0
if entireSet: # 遍歷整個數據集
for i in range(oS.m):
alphaPairsChanged += innerL(i, oS) # 使用優化的SMO演算法
print("全樣本遍歷:第%d次迭代 樣本:%d, alpha優化次數:%d" % (iter, i, alphaPairsChanged))
iter += 1
else: # 遍歷非邊界值
nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0] # 遍歷不在邊界0和C的alpha
for i in nonBoundIs:
alphaPairsChanged += innerL(i, oS)
print("非邊界遍歷:第%d次迭代 樣本:%d, alpha優化次數:%d" % (iter, i, alphaPairsChanged))
iter += 1
if entireSet: # 遍歷一次後改為非邊界遍歷
entireSet = False
elif (alphaPairsChanged == 0): # 如果alpha沒有更新,計算全樣本遍歷
entireSet = True
print("迭代次數: %d" % iter)
return oS.b, oS.alphas
#計算w的值
def calcWs(dataMat, labelMat, alphas):
X=mat(dataMat);labelMat=mat(labelMat).transpose()
m,n=shape(X)
#初始化w都為1
w=zeros((n,1))
#迴圈計算
for i in range(m):
w+=multiply(alphas[i]*labelMat[i],X[i,:].T)
return w
#核函數
def kernelTrans(X,A,kTup):
m,n=shape(X)
K=mat(zeros((m,1)))
if kTup[0]=='lin':#線性核
K=X*A.T
elif kTup[0] == 'rbf':#高斯核
for j in range(m):
deltaRow = X[j,:]-A
K[j]=deltaRow*deltaRow.T
K = exp(K/(-2*kTup[1]**2))
else:
raise NameError("Houston we Have a Problem--\ That Kernel is not recognized")
return K
#畫圖
def showClassifer(dataMat, labelMat, b,alphas,w):
fig=plt.figure()
ax=fig.add_subplot(111)
cm_dark=mpl.colors.ListedColormap(['g','r'])
ax.scatter(array(dataMat)[:,0],array(dataMat)[:,1],c=array(labelMat).squeeze(),cmap=cm_dark,s=30)
#畫決策平面
# x=arange(-2.0,12.0,0.1)
# y=(-w[0]*x-b)/w[1]
# ax.plot(x,y.reshape(-1,1))
# ax.axis([-2,12,-8,6])
#畫支持向量
alphas_non_zeros_index=where(alphas>0)
for i in alphas_non_zeros_index[0]:
circle= Circle((dataMat[i][0],dataMat[i][1]),0.03,facecolor='none',edgecolor=(0,0.8,0.8),linewidth=3,alpha=0.5)
ax.add_patch(circle)
plt.show()
if __name__ == '__main__':
dataMat, labelMat = loadDataSet('testSetRBF.txt')
b,alphas=smoSimple(dataMat,labelMat,0.6,0.001,40)
w = calcWs(dataMat, labelMat, alphas)
showClassifer(dataMat, labelMat, b,alphas,w)
運行結果