首先聲明,本文參照(7條消息) 【中文】【吳恩達課後編程作業】Course 1 - 神經網路和深度學習 - 第三周作業_何寬的博客-CSDN博客_吳恩達課後編程作業(https://blog.csdn.net/u013733326/article/details/79702148) 本文所使用的資料 ...
首先聲明,本文參照(7條消息) 【中文】【吳恩達課後編程作業】Course 1 - 神經網路和深度學習 - 第三周作業_何寬的博客-CSDN博客_吳恩達課後編程作業(https://blog.csdn.net/u013733326/article/details/79702148)
本文所使用的資料已上傳到百度網盤**【點擊下載】**,提取碼:qifu,請在開始之前下載好所需資料。當然還是需要將數據集放置在與代碼同一層次。
加上自己的理解,方便自己以後的學習
我們需要準備一些軟體包:
import numpy as np import matplotlib.pyplot as plt from testCases import * import sklearn import sklearn.datasets import sklearn.linear_model from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets np.random.seed(1) #設置一個固定的隨機種子,以保證接下來的步驟中我們的結果是一致的(所取的隨機值是一樣的)。
我們來看看我們將要使用的數據集, 下麵的代碼會將一個花的圖案的2類數據集載入到變數X和Y中
X, Y = load_planar_dataset()
plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral) #繪製散點圖 plt.show()

數據看起來像一朵紅色(y = 0)和一些藍色(y = 1)的數據點的花朵的圖案。 我們的目標是建立一個模型來適應這些數據。現在,我們已經有了以下的東西:
X:一個numpy的矩陣,包含了這些數據點的數值
Y:一個numpy的向量,對應著的是X的標簽【0 | 1】(紅色:0 , 藍色 :1)
我們繼續來仔細地看數據:
shape_X = X.shape shape_Y = Y.shape m = Y.shape[1] # 訓練集裡面的數量 print ("X的維度為: " + str(shape_X)) print ("Y的維度為: " + str(shape_Y)) print ("數據集裡面的數據有:" + str(m) + " 個")
X的維度為: (2, 400) Y的維度為: (1, 400) 數據集裡面的數據有:400 個
在構建完整的神經網路之前,先讓我們看看邏輯回歸在這個問題上的表現如何,我們可以使用sklearn的內置函數來做到這一點, 運行下麵的代碼來訓練數據集上的邏輯回歸分類器。
clf = sklearn.linear_model.LogisticRegressionCV()
clf.fit(X.T,Y.T)
會列印出這樣一段字:
E:\anaconda\lib\site-packages\sklearn\utils\validation.py:993: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel(). y = column_or_1d(y, warn=True)
#原型plot_decision_boundary(modle,x,y)對x進行預測,大於0.5取紅色,小於0.5取藍色 plot_decision_boundary(lambda x: clf.predict(x), X, Y) #繪製決策邊界 plt.title("Logistic Regression") #圖標題 LR_predictions = clf.predict(X.T) #預測結果 #Y的取值只有(0,1)所以這裡要用“+” print ("邏輯回歸的準確性: %d " % float((np.dot(Y, LR_predictions) + np.dot(1 - Y,1 - LR_predictions)) / float(Y.size) * 100) + "% " + "(正確標記的數據點所占的百分比)")
邏輯回歸的準確性: 47 % (正確標記的數據點所占的百分比)

準確性只有47%的原因是數據集不是線性可分的,所以邏輯回歸表現不佳,現在我們正式開始構建神經網路。(跟沒分類一樣,50%是最不好的分類情況)
搭建神經網路
隱藏層我們採取的是tanh函數,其導數為1-(tanh)^2

對於x(i)而言
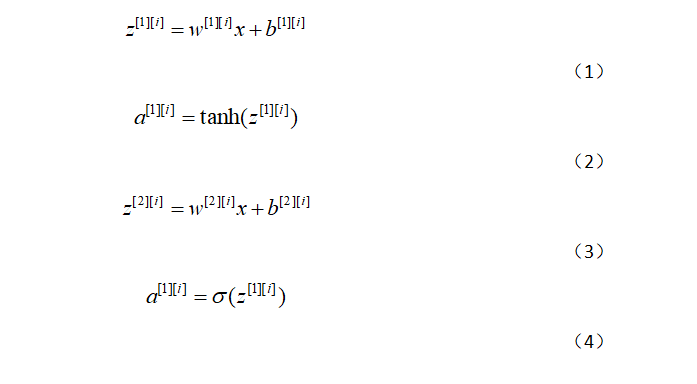
給出所有示例的預測結果,可以按如下方式計算成本J:

構建神經網路的一般方法是:
- 定義神經網路結構(輸入單元的數量,隱藏單元的數量等)。
- 初始化模型的參數
- 迴圈:
- 實施前向傳播
- 計算損失
- 實現向後傳播
- 更新參數(梯度下降)
我們要它們合併到一個nn_model() 函數中,當我們構建好了nn_model()並學習了正確的參數,我們就可以預測新的數據。
- n_x: 輸入層的數量
- n_h: 隱藏層的數量(這裡設置為4)當然可以設置為其他
- n_y: 輸出層的數量
def layer_sizes(X , Y): """ 參數: X - 輸入數據集,維度為(輸入的數量,訓練/測試的數量) Y - 標簽,維度為(輸出的數量,訓練/測試數量) 返回: n_x - 輸入層的數量 n_h - 隱藏層的數量 n_y - 輸出層的數量 """ n_x = X.shape[0] #輸入層 n_h = 4 #,隱藏層,硬編碼為4 n_y = Y.shape[0] #輸出層 return (n_x,n_h,n_y)
接下來,我們測試一下
#測試layer_sizes print("=========================測試layer_sizes=========================") X_asses , Y_asses = layer_sizes_test_case() (n_x,n_h,n_y) = layer_sizes(X_asses,Y_asses) print("輸入層的節點數量為: n_x = " + str(n_x)) print("隱藏層的節點數量為: n_h = " + str(n_h)) print("輸出層的節點數量為: n_y = " + str(n_y))
=========================測試layer_sizes========================= 輸入層的節點數量為: n_x = 5 隱藏層的節點數量為: n_h = 4 輸出層的節點數量為: n_y = 2
初始化模型的參數
在這裡,我們要實現函數initialize_parameters()。我們要確保我們的參數大小合適,如果需要的話,請參考上面的神經網路圖。
我們將會用隨機值初始化權重矩陣。
- np.random.randn(a,b)* 0.01來隨機初始化一個維度為(a,b)的矩陣
將偏向量初始化為零。
- np.zeros((a,b))用零初始化矩陣(a,b)
這裡做一下解釋,為什麼要乘以0.01
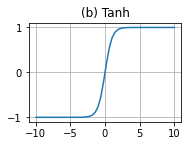
如圖,乘以的數越大,增長的速率越慢,因此我們採用0.01.
我們繼續走
def initialize_parameters( n_x , n_h ,n_y): """ 參數: n_x - 輸入層節點的數量 n_h - 隱藏層節點的數量 n_y - 輸出層節點的數量 返回: parameters - 包含參數的字典: W1 - 權重矩陣,維度為(n_h,n_x) b1 - 偏向量,維度為(n_h,1) W2 - 權重矩陣,維度為(n_y,n_h) b2 - 偏向量,維度為(n_y,1) """ np.random.seed(2) #指定一個隨機種子,以便你的輸出與我們的一樣。 W1 = np.random.randn(n_h,n_x) * 0.01 b1 = np.zeros(shape=(n_h, 1)) W2 = np.random.randn(n_y,n_h) * 0.01 b2 = np.zeros(shape=(n_y, 1)) #使用斷言確保我的數據格式是正確的 assert(W1.shape == ( n_h , n_x )) assert(b1.shape == ( n_h , 1 )) assert(W2.shape == ( n_y , n_h )) assert(b2.shape == ( n_y , 1 )) parameters = {"W1" : W1, "b1" : b1, "W2" : W2, "b2" : b2 } return parameters
我們來測試一下
#測試initialize_parameters print("=========================測試initialize_parameters=========================") n_x , n_h , n_y = initialize_parameters_test_case() parameters = initialize_parameters(n_x , n_h , n_y) print("W1 = " + str(parameters["W1"])) print("b1 = " + str(parameters["b1"])) print("W2 = " + str(parameters["W2"])) print("b2 = " + str(parameters["b2"]))
=========================測試initialize_parameters========================= W1 = [[-0.00416758 -0.00056267] [-0.02136196 0.01640271] [-0.01793436 -0.00841747] [ 0.00502881 -0.01245288]] b1 = [[0.] [0.] [0.] [0.]] W2 = [[-0.01057952 -0.00909008 0.00551454 0.02292208]] b2 = [[0.]]
迴圈
前向傳播
我們現在要實現前向傳播函數forward_propagation()。
我們可以使用sigmoid()函數,也可以使用np.tanh()函數。
步驟如下:
def forward_propagation( X , parameters ): """ 參數: X - 維度為(n_x,m)的輸入數據。 parameters - 初始化函數(initialize_parameters)的輸出 返回: A2 - 使用sigmoid()函數計算的第二次激活後的數值 cache - 包含“Z1”,“A1”,“Z2”和“A2”的字典類型變數 """ W1 = parameters["W1"] b1 = parameters["b1"] W2 = parameters["W2"] b2 = parameters["b2"] #前向傳播計算A2 Z1 = np.dot(W1 , X) + b1 A1 = np.tanh(Z1) Z2 = np.dot(W2 , A1) + b2 A2 = sigmoid(Z2) #使用斷言確保我的數據格式是正確的 assert(A2.shape == (1,X.shape[1])) cache = {"Z1": Z1, "A1": A1, "Z2": Z2, "A2": A2} return (A2, cache)
我們測試一下:
#測試forward_propagation print("=========================測試forward_propagation=========================") X_assess, parameters = forward_propagation_test_case() A2, cache = forward_propagation(X_assess, parameters) print(np.mean(cache["Z1"]), np.mean(cache["A1"]), np.mean(cache["Z2"]), np.mean(cache["A2"]))
=========================測試forward_propagation========================= -0.0004997557777419902 -0.000496963353231779 0.00043818745095914653 0.500109546852431
計算損失
def compute_cost(A2,Y,parameters): """ 計算方程(5)中給出的交叉熵成本, 參數: A2 - 使用sigmoid()函數計算的第二次激活後的數值 Y - "True"標簽向量,維度為(1,數量) parameters - 一個包含W1,B1,W2和B2的字典類型的變數 返回: 成本 - 交叉熵成本給出方程(13) """ m = Y.shape[1] W1 = parameters["W1"] W2 = parameters["W2"] #計算成本 logprobs = logprobs = np.multiply(np.log(A2), Y) + np.multiply((1 - Y), np.log(1 - A2)) cost = - np.sum(logprobs) / m cost = float(np.squeeze(cost)) assert(isinstance(cost,float)) return cost
測試一下我們的成本函數:
#測試compute_cost print("=========================測試compute_cost=========================") A2 , Y_assess , parameters = compute_cost_test_case() print("cost = " + str(compute_cost(A2,Y_assess,parameters)))
=========================測試compute_cost========================= cost = 0.6929198937761266
使用正向傳播期間計算的cache,現在可以利用它實現反向傳播。
現在我們要開始實現函數backward_propagation()。
向後傳播
這裡的公式還是比較複雜的,最好是自己推導一下,方便記憶
def backward_propagation(parameters,cache,X,Y): """ 使用上述說明搭建反向傳播函數。 參數: parameters - 包含我們的參數的一個字典類型的變數。 cache - 包含“Z1”,“A1”,“Z2”和“A2”的字典類型的變數。 X - 輸入數據,維度為(2,數量) Y - “True”標簽,維度為(1,數量) 返回: grads - 包含W和b的導數一個字典類型的變數。 """ m = X.shape[1] W1 = parameters["W1"] W2 = parameters["W2"] A1 = cache["A1"] A2 = cache["A2"] dZ2= A2 - Y dW2 = (1 / m) * np.dot(dZ2, A1.T) db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True) dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2)) dW1 = (1 / m) * np.dot(dZ1, X.T) db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True) grads = {"dW1": dW1, "db1": db1, "dW2": dW2, "db2": db2 } return grads
測試一下反向傳播函數:
#測試backward_propagation print("=========================測試backward_propagation=========================") parameters, cache, X_assess, Y_assess = backward_propagation_test_case() grads = backward_propagation(parameters, cache, X_assess, Y_assess) print ("dW1 = "+ str(grads["dW1"])) print ("db1 = "+ str(grads["db1"])) print ("dW2 = "+ str(grads["dW2"])) print ("db2 = "+ str(grads["db2"]))
=========================測試backward_propagation========================= dW1 = [[ 0.01018708 -0.00708701] [ 0.00873447 -0.0060768 ] [-0.00530847 0.00369379] [-0.02206365 0.01535126]] db1 = [[-0.00069728] [-0.00060606] [ 0.000364 ] [ 0.00151207]] dW2 = [[ 0.00363613 0.03153604 0.01162914 -0.01318316]] db2 = [[0.06589489]]
更新參數
def update_parameters(parameters,grads,learning_rate=1.2): """ 使用上面給出的梯度下降更新規則更新參數 參數: parameters - 包含參數的字典類型的變數。 grads - 包含導數值的字典類型的變數。 learning_rate - 學習速率 返回: parameters - 包含更新參數的字典類型的變數。 """ W1,W2 = parameters["W1"],parameters["W2"] b1,b2 = parameters["b1"],parameters["b2"] dW1,dW2 = grads["dW1"],grads["dW2"] db1,db2 = grads["db1"],grads["db2"] W1 = W1 - learning_rate * dW1 b1 = b1 - learning_rate * db1 W2 = W2 - learning_rate * dW2 b2 = b2 - learning_rate * db2 parameters = {"W1": W1, "b1": b1, "W2": W2, "b2": b2} return parameters
我們測試一下update_parameters():
#測試update_parameters print("=========================測試update_parameters=========================") parameters, grads = update_parameters_test_case() parameters = update_parameters(parameters, grads) print("W1 = " + str(parameters["W1"])) print("b1 = " + str(parameters["b1"])) print("W2 = " + str(parameters["W2"])) print("b2 = " + str(parameters["b2"]))
=========================測試update_parameters========================= W1 = [[-0.00643025 0.01936718] [-0.02410458 0.03978052] [-0.01653973 -0.02096177] [ 0.01046864 -0.05990141]] b1 = [[-1.02420756e-06] [ 1.27373948e-05] [ 8.32996807e-07] [-3.20136836e-06]] W2 = [[-0.01041081 -0.04463285 0.01758031 0.04747113]] b2 = [[0.00010457]]
整合
我們現在把上面的東西整合到nn_model()中,神經網路模型必須以正確的順序使用先前的功能。
def nn_model(X,Y,n_h,num_iterations,print_cost=False): """ 參數: X - 數據集,維度為(2,示例數) Y - 標簽,維度為(1,示例數) n_h - 隱藏層的數量 num_iterations - 梯度下降迴圈中的迭代次數 print_cost - 如果為True,則每1000次迭代列印一次成本數值 返回: parameters - 模型學習的參數,它們可以用來進行預測。 """ np.random.seed(3) #指定隨機種子 n_x = layer_sizes(X, Y)[0] n_y = layer_sizes(X, Y)[2] parameters = initialize_parameters(n_x,n_h,n_y) W1 = parameters["W1"] b1 = parameters["b1"] W2 = parameters["W2"] b2 = parameters["b2"] for i in range(num_iterations): A2 , cache = forward_propagation(X,parameters) cost = compute_cost(A2,Y,parameters) grads = backward_propagation(parameters,cache,X,Y) parameters = update_parameters(parameters,grads,learning_rate = 0.5) if print_cost: if i%1000 == 0: print("第 ",i," 次迴圈,成本為:"+str(cost)) return parameters
老規矩,測試nn_model():
#測試nn_model print("=========================測試nn_model=========================") X_assess, Y_assess = nn_model_test_case() parameters = nn_model(X_assess, Y_assess, 4, num_iterations=10000, print_cost=False) print("W1 = " + str(parameters["W1"])) print("b1 = " + str(parameters["b1"])) print("W2 = " + str(parameters["W2"])) print("b2 = " + str(parameters["b2"]))
=========================測試nn_model=========================
W1 = [[-3.89167767 4.77541602] [-6.77960338 1.20272585] [-3.88338966 4.78028666] [ 6.77958203 -1.20272574]] b1 = [[ 2.11530892] [ 3.41221357] [ 2.11585732] [-3.41221322]] W2 = [[-2512.9093032 -2502.70799785 -2512.01655969 2502.65264416]] b2 = [[-22.29071761]]
預測
構建predict()來使用模型進行預測, 使用向前傳播來預測結果。
def predict(parameters,X): """ 使用學習的參數,為X中的每個示例預測一個類 參數: parameters - 包含參數的字典類型的變數。 X - 輸入數據(n_x,m) 返回 predictions - 我們模型預測的向量(紅色:0 /藍色:1) """ A2 , cache = forward_propagation(X,parameters) predictions = np.round(A2) return predictions
測試一下predict:
#測試predict print("=========================測試predict=========================") parameters, X_assess = predict_test_case() predictions = predict(parameters, X_assess) print("預測的平均值 = " + str(np.mean(predictions)))
=========================測試predict========================= 預測的平均值 = 0.6666666666666666
正式運行
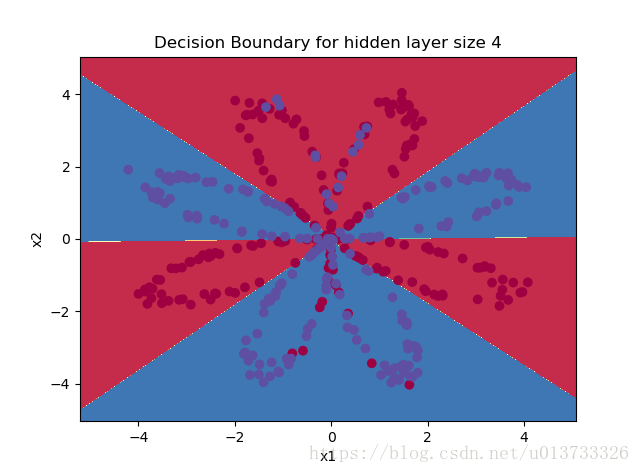
parameters = nn_model(X, Y, n_h = 4, num_iterations=10000, print_cost=True) #繪製邊界 plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y) plt.title("Decision Boundary for hidden layer size " + str(4)) predictions = predict(parameters, X) print ('準確率: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')
第 0 次迴圈,成本為:0.6930480201239823 第 1000 次迴圈,成本為:0.3098018601352803 第 2000 次迴圈,成本為:0.2924326333792646 第 3000 次迴圈,成本為:0.2833492852647412 第 4000 次迴圈,成本為:0.27678077562979253 第 5000 次迴圈,成本為:0.26347155088593144 第 6000 次迴圈,成本為:0.24204413129940763 第 7000 次迴圈,成本為:0.23552486626608762 第 8000 次迴圈,成本為:0.23140964509854278 第 9000 次迴圈,成本為:0.22846408048352365 準確率: 90%