摘要:圖像銳化和邊緣提取技術可以消除圖像中的雜訊,提取圖像信息中用來表徵圖像的一些變數,為圖像識別提供基礎。 本文分享自華為雲社區《[Python圖像處理] 十七.圖像銳化與邊緣檢測之Roberts運算元、Prewitt運算元、Sobel運算元和Laplacian算》,作者: eastmount 。 由於 ...
摘要:圖像銳化和邊緣提取技術可以消除圖像中的雜訊,提取圖像信息中用來表徵圖像的一些變數,為圖像識別提供基礎。
本文分享自華為雲社區《[Python圖像處理] 十七.圖像銳化與邊緣檢測之Roberts運算元、Prewitt運算元、Sobel運算元和Laplacian算》,作者: eastmount 。
由於收集圖像數據的器件或傳輸數圖像的通道的存在一些質量缺陷,文物圖像時間久遠,或者受一些其他外界因素、動態不穩定抓取圖像的影響,使得圖像存在模糊和有雜訊的情況,從而影響到圖像識別工作的開展。這時需要開展圖像銳化和邊緣檢測處理,加強原圖像的高頻部分,銳化突出圖像的邊緣細節,改善圖像的對比度,使模糊的圖像變得更清晰。
圖像銳化和邊緣提取技術可以消除圖像中的雜訊,提取圖像信息中用來表徵圖像的一些變數,為圖像識別提供基礎。通常使用灰度差分法對圖像的邊緣、輪廓進行處理,將其凸顯。本文分別採用Laplacian運算元、Robert運算元、Prewitt運算元和Sobel運算元進行圖像銳化邊緣處理實驗。本文主要講解灰度線性變換,基礎性知識希望對您有所幫助。
該系列在github所有源代碼:https://github.com/eastmountyxz/ImageProcessing-Python
一.Roberts運算元
Roberts運算元又稱為交叉微分演算法,它是基於交叉差分的梯度演算法,通過局部差分計算檢測邊緣線條。常用來處理具有陡峭的低雜訊圖像,當圖像邊緣接近於正45度或負45度時,該演算法處理效果更理想。其缺點是對邊緣的定位不太準確,提取的邊緣線條較粗。
Roberts運算元的模板分為水平方向和垂直方向,如公式(11.7)所示,從其模板可以看出,Roberts運算元能較好的增強正負45度的圖像邊緣。
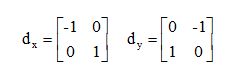
詳細計算公式如下所示:(PS-下圖參考自己的書和論文)

在Python中,Roberts運算元主要通過Numpy定義模板,再調用OpenCV的filter2D()函數實現邊緣提取。該函數主要是利用內核實現對圖像的捲積運算,其函數原型如下所示:
dst = filter2D(src, ddepth, kernel[, dst[, anchor[, delta[, borderType]]]])
- src表示輸入圖像
- dst表示輸出的邊緣圖,其大小和通道數與輸入圖像相同
- ddepth表示目標圖像所需的深度
- kernel表示捲積核,一個單通道浮點型矩陣
- anchor表示內核的基準點,其預設值為(-1,-1),位於中心位置
- delta表示在儲存目標圖像前可選的添加到像素的值,預設值為0
- borderType表示邊框模式
Python實現代碼如下所示:
# -*- coding: utf-8 -*- import cv2 import numpy as np import matplotlib.pyplot as plt #讀取圖像 img = cv2.imread('lena.png') lenna_img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB) #灰度化處理圖像 grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) #Roberts運算元 kernelx = np.array([[-1,0],[0,1]], dtype=int) kernely = np.array([[0,-1],[1,0]], dtype=int) x = cv2.filter2D(grayImage, cv2.CV_16S, kernelx) y = cv2.filter2D(grayImage, cv2.CV_16S, kernely) #轉uint8 absX = cv2.convertScaleAbs(x) absY = cv2.convertScaleAbs(y) Roberts = cv2.addWeighted(absX,0.5,absY,0.5,0) #用來正常顯示中文標簽 plt.rcParams['font.sans-serif']=['SimHei'] #顯示圖形 titles = [u'原始圖像', u'Roberts運算元'] images = [lenna_img, Roberts] for i in xrange(2): plt.subplot(1,2,i+1), plt.imshow(images[i], 'gray') plt.title(titles[i]) plt.xticks([]),plt.yticks([]) plt.show()
運行結果如下圖所示:
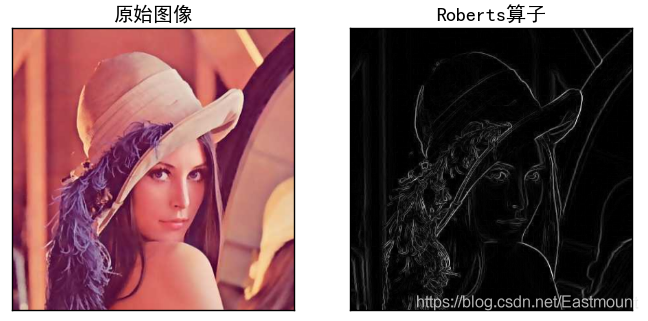
二.Prewitt運算元
Prewitt是一種圖像邊緣檢測的微分運算元,其原理是利用特定區域內像素灰度值產生的差分實現邊緣檢測。由於Prewitt運算元採用33模板對區域內的像素值進行計算,而Robert運算元的模板為22,故Prewitt運算元的邊緣檢測結果在水平方向和垂直方向均比Robert運算元更加明顯。Prewitt運算元適合用來識別雜訊較多、灰度漸變的圖像,其計算公式如下所示。
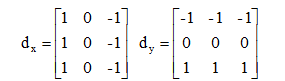
在Python中,Prewitt運算元的實現過程與Roberts運算元比較相似。通過Numpy定義模板,再調用OpenCV的filter2D()函數實現對圖像的捲積運算,最終通過convertScaleAbs()和addWeighted()函數實現邊緣提取,代碼如下所示:
# -*- coding: utf-8 -*- import cv2 import numpy as np import matplotlib.pyplot as plt #讀取圖像 img = cv2.imread('lena.png') lenna_img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB) #灰度化處理圖像 grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) #Prewitt運算元 kernelx = np.array([[1,1,1],[0,0,0],[-1,-1,-1]],dtype=int) kernely = np.array([[-1,0,1],[-1,0,1],[-1,0,1]],dtype=int) x = cv2.filter2D(grayImage, cv2.CV_16S, kernelx) y = cv2.filter2D(grayImage, cv2.CV_16S, kernely) #轉uint8 absX = cv2.convertScaleAbs(x) absY = cv2.convertScaleAbs(y) Prewitt = cv2.addWeighted(absX,0.5,absY,0.5,0) #用來正常顯示中文標簽 plt.rcParams['font.sans-serif']=['SimHei'] #顯示圖形 titles = [u'原始圖像', u'Prewitt運算元'] images = [lenna_img, Prewitt] for i in xrange(2): plt.subplot(1,2,i+1), plt.imshow(images[i], 'gray') plt.title(titles[i]) plt.xticks([]),plt.yticks([]) plt.show()
輸出結果如下圖所示,左邊為原始圖像,右邊為Prewitt運算元圖像銳化提取的邊緣輪廓,其效果圖的邊緣檢測結果在水平方向和垂直方向均比Robert運算元更加明顯。

三.Sobel運算元
Sobel運算元是一種用於邊緣檢測的離散微分運算元,它結合了高斯平滑和微分求導。該運算元用於計算圖像明暗程度近似值,根據圖像邊緣旁邊明暗程度把該區域內超過某個數的特定點記為邊緣。Sobel運算元在Prewitt運算元的基礎上增加了權重的概念,認為相鄰點的距離遠近對當前像素點的影響是不同的,距離越近的像素點對應當前像素的影響越大,從而實現圖像銳化並突出邊緣輪廓。
Sobel運算元的邊緣定位更準確,常用於雜訊較多、灰度漸變的圖像。其演算法模板如公式所示,其中dx表示水平方向,dy表示垂直方向。
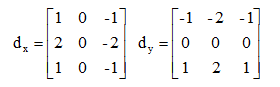
Sobel運算元根據像素點上下、左右鄰點灰度加權差,在邊緣處達到極值這一現象檢測邊緣。對雜訊具有平滑作用,提供較為精確的邊緣方向信息。因為Sobel運算元結合了高斯平滑和微分求導(分化),因此結果會具有更多的抗噪性,當對精度要求不是很高時,Sobel運算元是一種較為常用的邊緣檢測方法。
dst = Sobel(src, ddepth, dx, dy[, dst[, ksize[, scale[, delta[, borderType]]]]])
- src表示輸入圖像
- dst表示輸出的邊緣圖,其大小和通道數與輸入圖像相同
- ddepth表示目標圖像所需的深度,針對不同的輸入圖像,輸出目標圖像有不同的深度
- dx表示x方向上的差分階數,取值1或 0
- dy表示y方向上的差分階數,取值1或0
- ksize表示Sobel運算元的大小,其值必須是正數和奇數
- scale表示縮放導數的比例常數,預設情況下沒有伸縮繫數
- delta表示將結果存入目標圖像之前,添加到結果中的可選增量值
- borderType表示邊框模式,更多詳細信息查閱BorderTypes
註意,在進行Sobel運算元處理之後,還需要調用convertScaleAbs()函數計算絕對值,並將圖像轉換為8點陣圖進行顯示。其演算法原型如下:
dst = convertScaleAbs(src[, dst[, alpha[, beta]]])
- src表示原數組
- dst表示輸出數組,深度為8位
- alpha表示比例因數
- beta表示原數組元素按比例縮放後添加的值
Sobel運算元的實現代碼如下所示:
# -*- coding: utf-8 -*- import cv2 import numpy as np import matplotlib.pyplot as plt #讀取圖像 img = cv2.imread('lena.png') lenna_img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB) #灰度化處理圖像 grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) #Sobel運算元 x = cv2.Sobel(grayImage, cv2.CV_16S, 1, 0) #對x求一階導 y = cv2.Sobel(grayImage, cv2.CV_16S, 0, 1) #對y求一階導 absX = cv2.convertScaleAbs(x) absY = cv2.convertScaleAbs(y) Sobel = cv2.addWeighted(absX, 0.5, absY, 0.5, 0) #用來正常顯示中文標簽 plt.rcParams['font.sans-serif']=['SimHei'] #顯示圖形 titles = [u'原始圖像', u'Sobel運算元'] images = [lenna_img, Sobel] for i in xrange(2): plt.subplot(1,2,i+1), plt.imshow(images[i], 'gray') plt.title(titles[i]) plt.xticks([]),plt.yticks([]) plt.show()
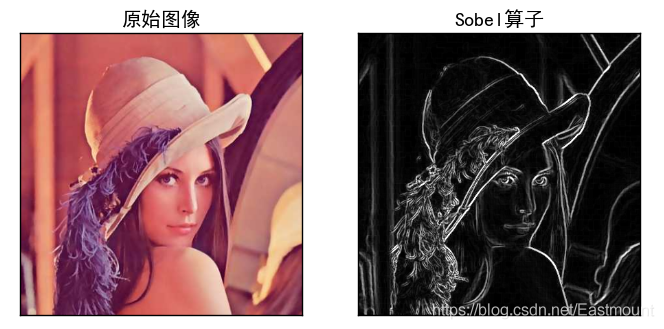
最終輸出結果如下圖所示:
四.Laplacian運算元
拉普拉斯(Laplacian)運算元是n維歐幾里德空間中的一個二階微分運算元,常用於圖像增強領域和邊緣提取。它通過灰度差分計算鄰域內的像素,基本流程是:判斷圖像中心像素灰度值與它周圍其他像素的灰度值,如果中心像素的灰度更高,則提升中心像素的灰度;反之降低中心像素的灰度,從而實現圖像銳化操作。在演算法實現過程中,Laplacian運算元通過對鄰域中心像素的四方向或八方向求梯度,再將梯度相加起來判斷中心像素灰度與鄰域內其他像素灰度的關係,最後通過梯度運算的結果對像素灰度進行調整。
Laplacian運算元分為四鄰域和八鄰域,四鄰域是對鄰域中心像素的四方向求梯度,八鄰域是對八方向求梯度。其中,四鄰域模板如公式所示:
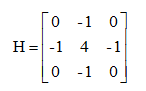
通過模板可以發現,當鄰域內像素灰度相同時,模板的捲積運算結果為0;當中心像素灰度高於鄰域內其他像素的平均灰度時,模板的捲積運算結果為正數;當中心像素的灰度低於鄰域內其他像素的平均灰度時,模板的捲積為負數。對捲積運算的結果用適當的衰弱因數處理並加在原中心像素上,就可以實現圖像的銳化處理。
Laplacian運算元的八鄰域模板如下:
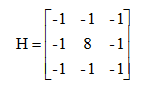
Python和OpenCV將Laplacian運算元封裝在Laplacian()函數中,其函數原型如下所示:
dst = Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]])
- src表示輸入圖像
- dst表示輸出的邊緣圖,其大小和通道數與輸入圖像相同
- ddepth表示目標圖像所需的深度
- ksize表示用於計算二階導數的濾波器的孔徑大小,其值必須是正數和奇數,且預設值為1,更多詳細信息查閱getDerivKernels
- scale表示計算拉普拉斯運算元值的可選比例因數。預設值為1,更多詳細信息查閱getDerivKernels
- delta表示將結果存入目標圖像之前,添加到結果中的可選增量值,預設值為0
- borderType表示邊框模式,更多詳細信息查閱BorderTypes
註意,Laplacian運算元其實主要是利用Sobel運算元的運算,通過加上Sobel運算元運算出的圖像x方向和y方向上的導數,得到輸入圖像的圖像銳化結果。同時,在進行Laplacian運算元處理之後,還需要調用convertScaleAbs()函數計算絕對值,並將圖像轉換為8點陣圖進行顯示。
當ksize=1時,Laplacian()函數採用3×3的孔徑(四鄰域模板)進行變換處理。下麵的代碼是採用ksize=3的Laplacian運算元進行圖像銳化處理,其代碼如下:
# -*- coding: utf-8 -*- import cv2 import numpy as np import matplotlib.pyplot as plt #讀取圖像 img = cv2.imread('lena.png') lenna_img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB) #灰度化處理圖像 grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) #拉普拉斯演算法 dst = cv2.Laplacian(grayImage, cv2.CV_16S, ksize = 3) Laplacian = cv2.convertScaleAbs(dst) #用來正常顯示中文標簽 plt.rcParams['font.sans-serif']=['SimHei'] #顯示圖形 titles = [u'原始圖像', u'Laplacian運算元'] images = [lenna_img, Laplacian] for i in xrange(2): plt.subplot(1,2,i+1), plt.imshow(images[i], 'gray') plt.title(titles[i]) plt.xticks([]),plt.yticks([]) plt.show()
最終輸出結果如下圖所示:

五.總結代碼
邊緣檢測演算法主要是基於圖像強度的一階和二階導數,但導數通常對雜訊很敏感,因此需要採用濾波器來過濾雜訊,並調用圖像增強或閾值化演算法進行處理,最後再進行邊緣檢測。下麵是採用高斯濾波去噪和閾值化處理之後,再進行邊緣檢測的過程,並對比了四種常見的邊緣提取演算法。
# -*- coding: utf-8 -*- import cv2 import numpy as np import matplotlib.pyplot as plt #讀取圖像 img = cv2.imread('lena.png') lenna_img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) #灰度化處理圖像 grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) #高斯濾波 gaussianBlur = cv2.GaussianBlur(grayImage, (3,3), 0) #閾值處理 ret, binary = cv2.threshold(gaussianBlur, 127, 255, cv2.THRESH_BINARY) #Roberts運算元 kernelx = np.array([[-1,0],[0,1]], dtype=int) kernely = np.array([[0,-1],[1,0]], dtype=int) x = cv2.filter2D(binary, cv2.CV_16S, kernelx) y = cv2.filter2D(binary, cv2.CV_16S, kernely) absX = cv2.convertScaleAbs(x) absY = cv2.convertScaleAbs(y) Roberts = cv2.addWeighted(absX, 0.5, absY, 0.5, 0) #Prewitt運算元 kernelx = np.array([[1,1,1],[0,0,0],[-1,-1,-1]], dtype=int) kernely = np.array([[-1,0,1],[-1,0,1],[-1,0,1]], dtype=int) x = cv2.filter2D(binary, cv2.CV_16S, kernelx) y = cv2.filter2D(binary, cv2.CV_16S, kernely) absX = cv2.convertScaleAbs(x) absY = cv2.convertScaleAbs(y) Prewitt = cv2.addWeighted(absX,0.5,absY,0.5,0) #Sobel運算元 x = cv2.Sobel(binary, cv2.CV_16S, 1, 0) y = cv2.Sobel(binary, cv2.CV_16S, 0, 1) absX = cv2.convertScaleAbs(x) absY = cv2.convertScaleAbs(y) Sobel = cv2.addWeighted(absX, 0.5, absY, 0.5, 0) #拉普拉斯演算法 dst = cv2.Laplacian(binary, cv2.CV_16S, ksize = 3) Laplacian = cv2.convertScaleAbs(dst) #效果圖 titles = ['Source Image', 'Binary Image', 'Roberts Image', 'Prewitt Image','Sobel Image', 'Laplacian Image'] images = [lenna_img, binary, Roberts, Prewitt, Sobel, Laplacian] for i in np.arange(6): plt.subplot(2,3,i+1),plt.imshow(images[i],'gray') plt.title(titles[i]) plt.xticks([]),plt.yticks([]) plt.show()
輸出結果如圖所示。其中,Laplacian運算元對雜訊比較敏感,由於其演算法可能會出現雙像素邊界,常用來判斷邊緣像素位於圖像的明區或暗區,很少用於邊緣檢測;Robert運算元對陡峭的低雜訊圖像效果較好,尤其是邊緣正負45度較多的圖像,但定位準確率較差;Prewitt運算元對灰度漸變的圖像邊緣提取效果較好,而沒有考慮相鄰點的距離遠近對當前像素點的影響;Sobel運算元考慮了綜合因素,對雜訊較多的圖像處理效果更好。




