1.樹的基礎知識概述 樹狀圖是一種數據結構,它是由 n(n>=1)個有限結點組成一個具有層次關係的集合。把它叫做“樹”是因為它看起來像一棵倒掛的樹,也就是說它是根朝上,而葉朝下的。它具有以下的特點:每個結點有零個或多個子結點;沒有父結點的結點稱為根結點;每一個非根結點有且只有一個父結點;除了根結點外 ...
1.樹的基礎知識概述
樹狀圖是一種數據結構,它是由 n(n>=1)個有限結點組成一個具有層次關係的集合。把它叫做“樹”是因為它看起來像一棵倒掛的樹,也就是說它是根朝上,而葉朝下的。它具有以下的特點:
每個結點有零個或多個子結點;沒有父結點的結點稱為根結點;每一個非根結點有且只有一個父結點;除了根結點外,每個子結點可以分為多個不相交的子樹;
| 專業術語 | 中 文 | 描 述 |
|
Root |
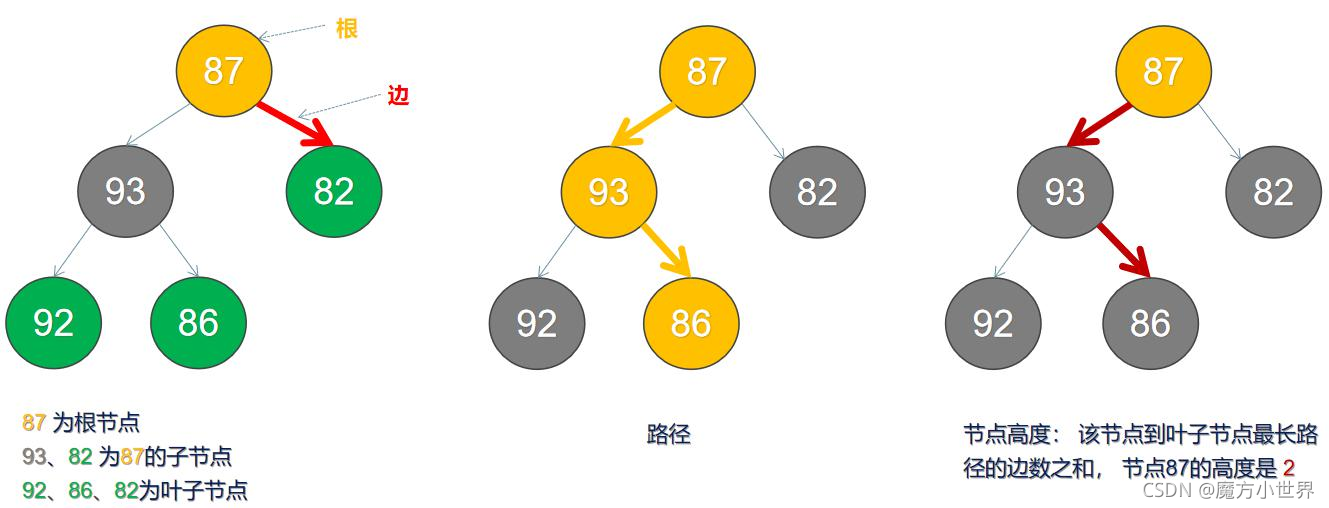
根節點 | 一棵樹的頂點 |
| Child | 孩子節點 | 一個結點含有的子樹的根結點稱為該結點的子結點 |
| Leaf | 葉子節點 | 沒有孩子的節點(度為0) |
| Degree | 度 | 一個節點包含的子樹的數量 |
| Edge | 邊 | 一個節點與另外一個節點的連接 |
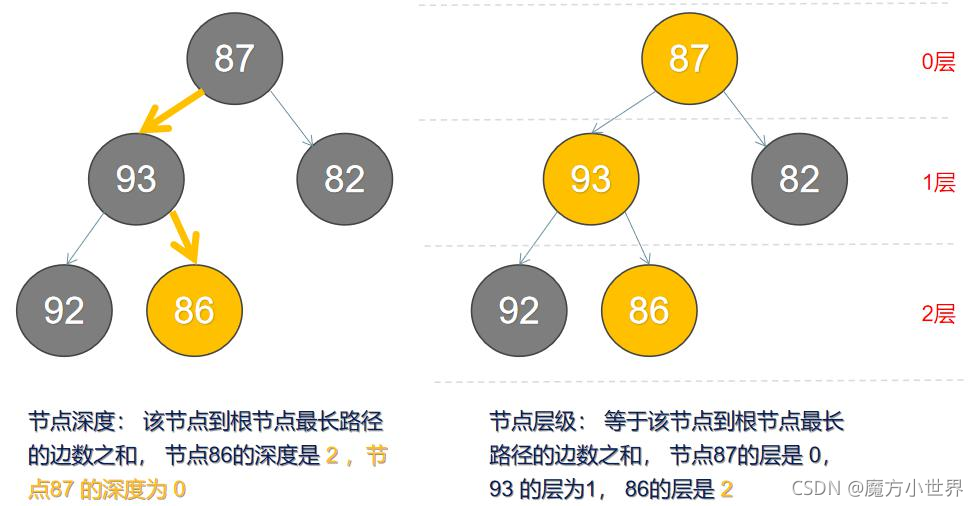
| Depth | 深度 | 根節點到這個節點經過的邊的數量 |
| Height | 節點高度 | 從當前節點到葉子節點形成路徑中邊的數量 |
| Level | 層級 | 節點到根節點最長路徑的邊的總和 |
| Path | 路徑 |
一個節點和另一個節點之間經過的邊和 Node 的序列 |
2.二叉樹
2.1二叉樹的基本概念
二叉樹是n(n≥0)個結點的有限集合,該集合或者為空集(空二叉樹),或者由一個根結點和兩個互不相交的、分別稱為根結點左子樹和右子樹的二叉樹組成。
二叉樹是一個每個結點最多只能有兩個分支的樹,左邊的分支稱之為左子樹,右邊的分支稱之為右子樹。
(1)在風控二叉樹,第i-1層的結點總數不超過,i>=1; (2)深度為h-1的二叉樹最多有-1個結點(h>=1),最少有h個結點 (3)對於任意一棵二叉樹,如果葉節點為N0,而度數為2 的結點總數為N2,則N0=N2+1;
每個度為1的結點有1條邊,度為2的結點有兩條邊。所以總邊數為1*n1+2*n2,總邊數等於結點數減1,即 N-1 = 1*n1+2*n2。其中總結點數又等於度為1、度為2、度為0的結點數和,即 N = n1 + n2 + n0;聯立可得N0=N2+1。
2.2二叉樹的特點
1.每個結點最多有兩個子樹,所以二叉樹中不存在度大於2的結點。 2.左子樹和右子樹是有順序的,次序不能顛倒。即使樹中只有一顆子樹,也要區分是左子樹還是右子樹。
2.3二叉樹的五種形態
1.空二叉樹。 2.只有一個根結點。 3.根結點只有左子樹。 4.根結點只有右子樹。 5.根結點既有左子樹,又有右子樹。
2.4特殊二叉樹
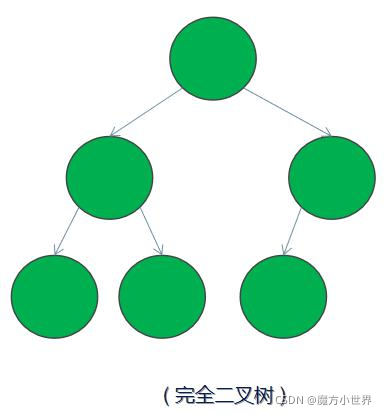
1)完全二叉樹 ——若設二叉樹的高度為 h,除第 h 層外,其它各層 (1~h-1) 的結點數都達到最大個數,第 h 層有葉子節點,並且葉子結點都是從左到右依次排布,這就是完全二叉樹(堆就是完全二叉樹)。
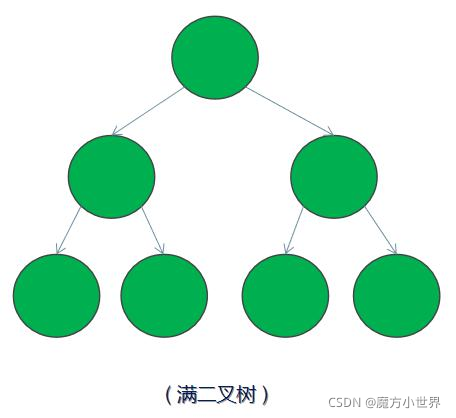
2)滿二叉樹 ——除了葉結點外每一個結點都有左右子節點且葉子結點都處在最底層的二叉樹。
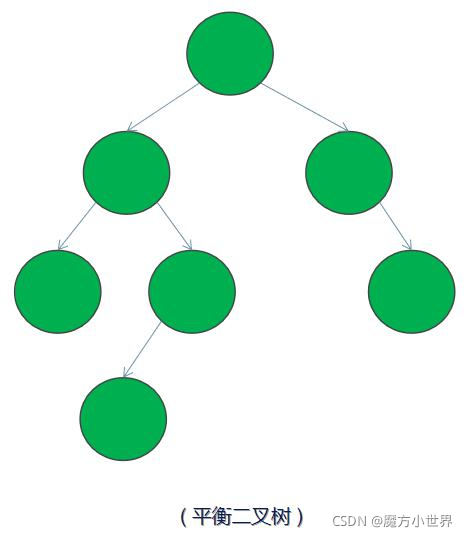
3)平衡二叉樹 ——又被稱為 AVL 樹,它是一顆空樹或左右兩個子樹的高度差的絕對值不超過 1,並且左右兩個子樹都是一棵平衡二叉樹。
4)二叉搜索樹 ——又稱二叉查找樹、二叉排序樹(Binary Sort Tree)。它是一顆空樹或是滿足下列性質的二叉樹:(右邊>=根>=左邊) 1)若左子樹不空,則左子樹上所有節點的值均小於或等於它的根節點的值; 2)若右子樹不空,則右子樹上所有節點的值均大於或等於它的根節點的值; 3)左、右子樹也分別為二叉排序樹。

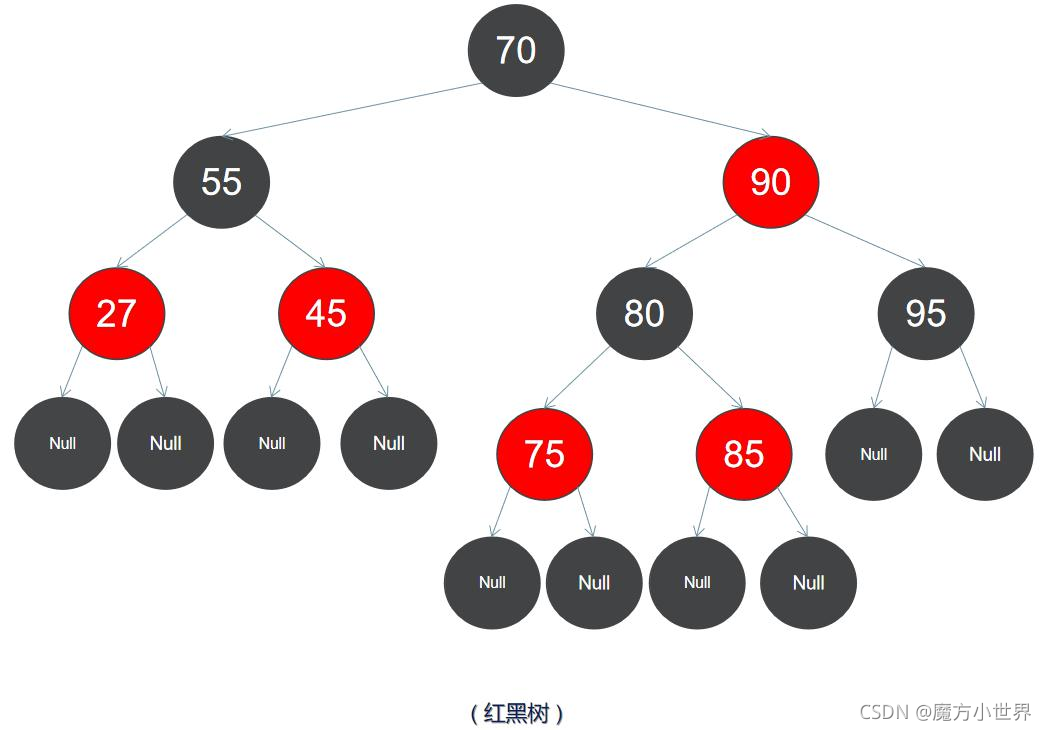
5)紅黑樹 ——是每個節點都帶有顏色屬性(顏色為紅色或黑色)的自平衡二叉查找樹,滿足下列性質: 1)節點是紅色或黑色; 2)根節點是黑色; 3)所有葉子節點都是黑色; 4)每個紅色節點必須有兩個黑色的子節點。(從每個葉子到根的所有路徑上不能有兩個 連續為紅色的結點); 5)從任一節點到其每個葉子的所有簡單路徑都包含相同數目的黑色節點。 (沒有度為 1的結點)。 以上規則可以保證左右子樹結點數差距不超過兩倍~
2.5二叉樹的性質
1.在二叉樹的第i層上最多有2i-1個結點(i≥1)。 2.深度為k的二叉樹最多有2k-1個結點(k≥1)。 3.對於任何一個二叉樹,如果其葉子結點數為n0,度數為2的結點數為n2,那麼n0=n2+1,也就是葉子結點數為度為2的結點數加1。 4.具有n個結點的完全二叉樹深度為(log2n)+1。 5.對具有n個結點的完全二叉樹,如果按照從上至下和從左至右的順序對二叉樹的所有結點從1開始編號,則對於任意的序號為i的結點有: A. 如果i>1,那麼序號為i的結點的雙親結點序號為i/2; B. 如果i=1,那麼序號為i的結點為根節點,無雙親結點; C. 如果2i<=n,那麼序號為i的結點的左孩子結點序號為2i; D. 如果2i>n,那麼序號為i的結點無左孩子; E. 如果2i+1<=n,那麼序號為i的結點右孩子序號為2i+1; F. 如果2i+1>n,那麼序號為i的結點無右孩子。
3.二叉搜索樹的演算法實現
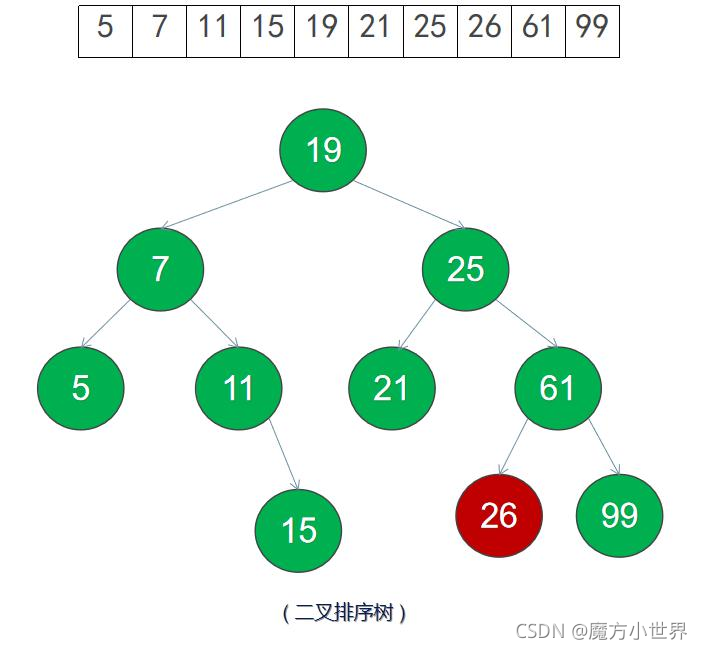
比如有以下數據:

當我們想保證查找效率時,可以用順序表存儲,當我們想保證插入和刪除效率時,我們可以用鏈式表存儲,有沒有一種存儲方法可以同時兼顧順序表和鏈式表的優點?
使用二叉樹,便可兼顧查找效率和插入刪除效率~
二叉樹一般採用鏈式存儲方式:每個結點包含兩個指針域,指向兩個孩子結點,還包含一個數據域,存儲結點信息。

結點結構體定義:
1 typedef struct _BNode { 2 int data; 3 struct _BNode *lchild, *rchild; 4 }Bnode,*Btree;
3.1二叉搜索樹插入結點
1 2 //二叉樹插入結點 3 /*將插入結點e,與結點root結點進行比較,若小於則去到左子樹,否則 4 去右子樹進行比較,重覆以上操作直到找到一個空位置放置該結點 5 */ 6 bool InsertBtree(Btree* root, Bnode* node) { 7 Bnode* temp = NULL; 8 Bnode* parent = NULL; 9 if (!node) { //如果插入結點為空,返回false 10 return false; 11 }else { //清空插入結點的左右子樹 12 node->lchild = NULL; 13 node->rchild = NULL; 14 } 15 16 if (!(*root)) { //如果根節點不存在,將插入結點作為根節點 17 *root = node; 18 return true; 19 }else { 20 temp = *root; 21 } 22 23 while (temp != NULL) { 24 parent = temp; 25 if (temp->data>node->data) { //小於,繼續向左 26 temp = temp->lchild; 27 } 28 else { //大於,繼續向右(不可以有相同的值) 29 temp=temp->rchild; 30 } 31 //while迴圈結束,parent所處位置即為要插入結點的父結點 32 } 33 if (node->data < parent->data) { 34 parent->lchild = node; 35 } 36 else { 37 parent->rchild = node; 38 } 39 return true; 40 }
3.2二叉搜索樹刪除結點
將要刪除的節點的值,與節點 root 節點進行比較,若小於則去到左子樹進行比較,若大於則去到右子樹進行比較,重覆以上操作直到找到一個節點的值等於刪除的值,則將此節點刪除。刪除時有 4 中情況須分別處理:
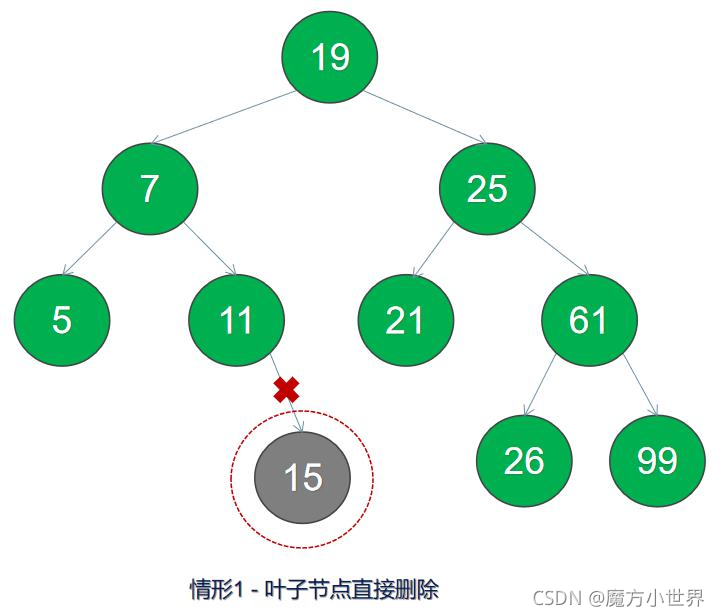
1.刪除節點不存在左右子節點,即為葉子節點,直接刪除
2.刪除節點存在左子節點,不存在右子節點,直接把左子節點替代刪除節點
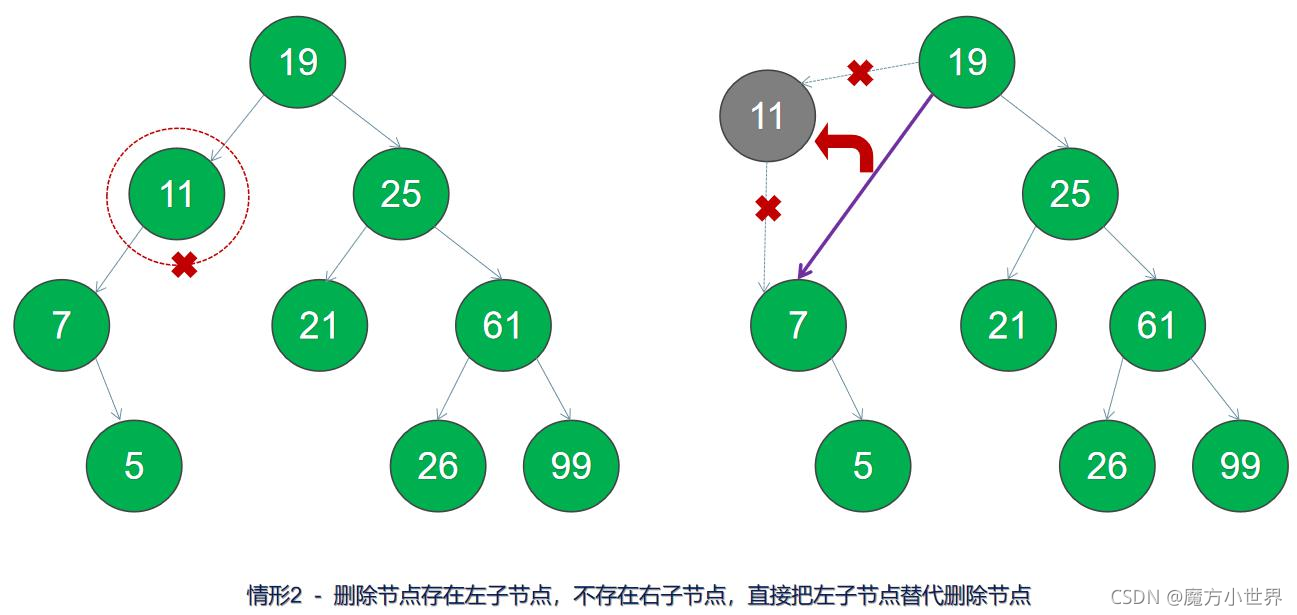
3.刪除節點存在右子節點,不存在左子節點,直接把右子節點替代刪除節點
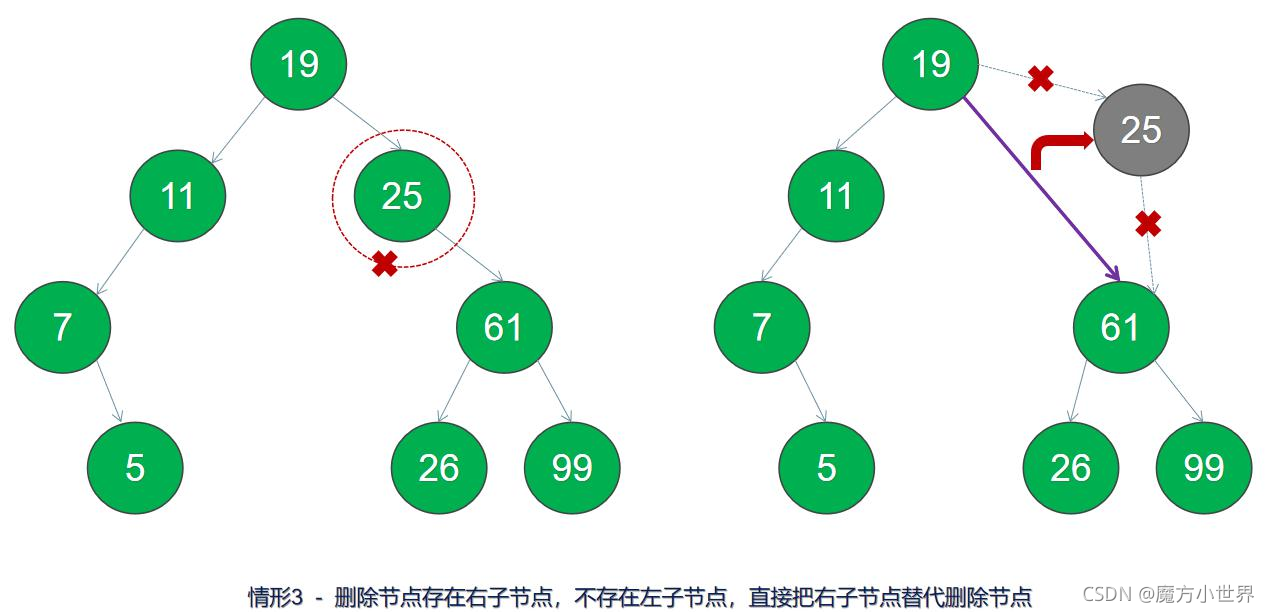
4.刪除節點存在左右子節點,則取左子樹上的最大節點或右子樹上的最小節點替換刪除節點。
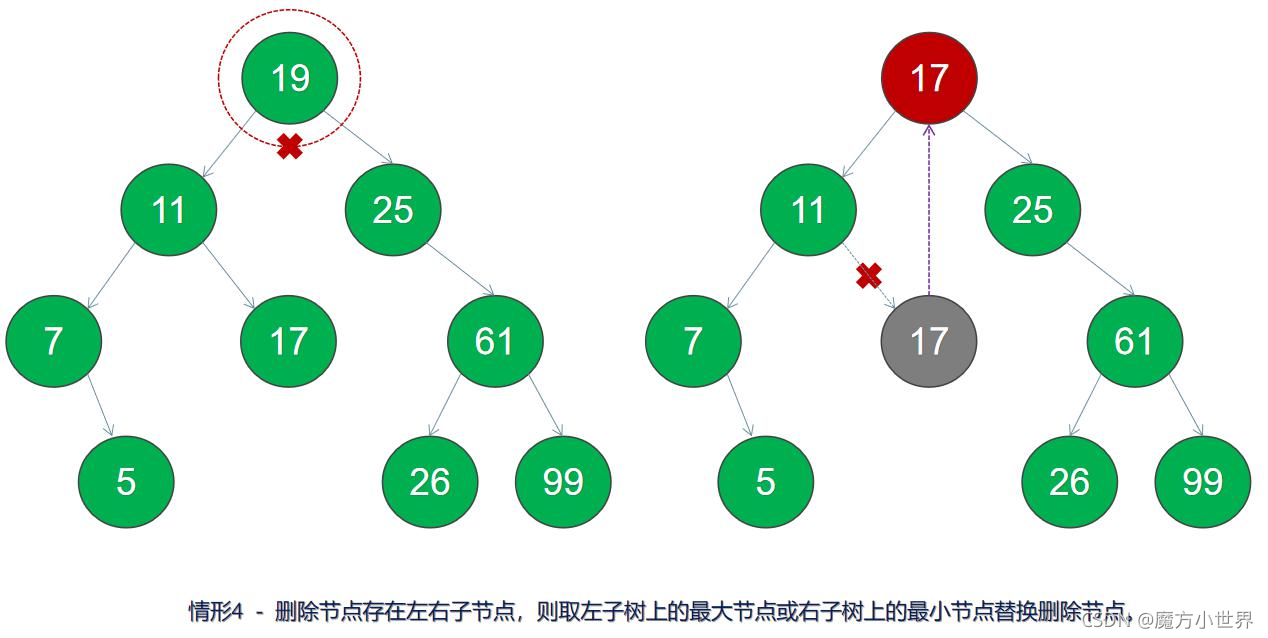
代碼實現:
1 //查找左子樹最大值 2 int findLeftMax(Btree* root) { 3 /*採用遞歸方式查找 4 * if (root->rchild == NULL) 5 return root->data; 6 return findMax(root->rchild); 7 */ 8 //採用迴圈查找 9 Btree indexNode = *root; 10 while (indexNode->rchild) 11 indexNode = indexNode->rchild; 12 return indexNode->data; 13 } 14 15 16 //採用遞歸的方式刪除結點 17 /* 18 這種遞歸方式,是將要修改的結點的一層一層的返回 19 */ 20 Btree deleteNode(Btree* root, int value) { 21 Btree compareNode = *root; 22 //節點為空(遞歸找不到value/根節點為空),直接返回 23 if (!compareNode)return compareNode; 24 //大於 25 if (compareNode->data > value) { 26 //左子樹重新被賦值 27 compareNode->lchild = deleteNode(&(compareNode->lchild), value); 28 return compareNode; 29 } 30 //小於 31 else if (compareNode->data < value) { 32 //右子樹重新被賦值 33 compareNode->rchild = deleteNode(&(compareNode->rchild), value); 34 return compareNode; 35 } 36 else {//等於 37 Btree temp = NULL; 38 //無左右子節點,直接返回NULL 39 if (compareNode->lchild == NULL && compareNode->rchild == NULL) { 40 delete compareNode; 41 } 42 //有左子樹,返回左子樹 43 else if (compareNode->lchild && compareNode->rchild == NULL) { 44 temp = compareNode->lchild; 45 delete compareNode; 46 } 47 //有右子樹,返回右子樹 48 else if (compareNode->rchild && compareNode->lchild == NULL) { 49 temp = compareNode->rchild; 50 delete compareNode; 51 } 52 else { 53 //這裡採用左子樹最大值替換 54 int leftMax = findLeftMax(&(compareNode->lchild)); 55 //最大值替換刪除結點的值 56 compareNode->data = leftMax; 57 //將最大值從樹中刪除 58 compareNode->lchild = deleteNode(&(compareNode->lchild), leftMax); 59 temp= compareNode; 60 } 61 return temp; 62 } 63 }
3.3二叉搜索樹查找
1 // 採用遞歸方式查找結點 2 /* 3 Bnode* queryByRec(Btree root, int value) { 4 if (root == NULL || root->data==value ){ 5 return root; 6 } 7 else if (root->data < value) { 8 return queryByRec(root->lchild, value); 9 } 10 else { 11 return queryByRec(root->rchild, value); 12 } 13 }*/ 14 15 // 使用非遞歸方式查找結點 16 17 Bnode* queryByLoop(Btree root, int value) { 18 while (root != NULL && root->data!=value) { 19 if (root->data>value) { 20 root = root->lchild; 21 } 22 else { 23 root = root->rchild; 24 } 25 } 26 return root; 27 }
3.4二叉搜索樹遍歷結點
3.4.1前序遍歷
前序遍歷,簡單來說就是遍歷根-左孩子-右孩子
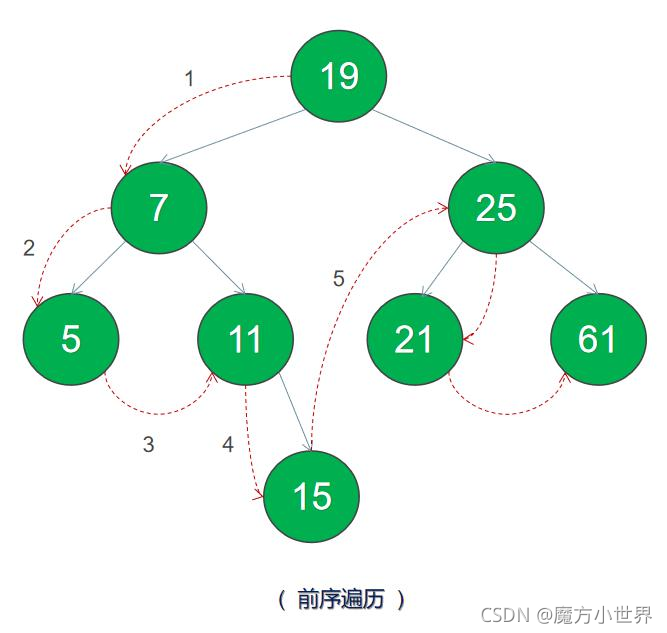
如上圖,前序遍歷的結果為 19 7 5 11 15 25 21 61
1 void PreOrderRec(int x)//x為根節點 2 { 3 if (x == 0)return;//若遍歷完成,返回函數 4 cout<<x; 5 PreOrderRec(a[x].left);//遍歷左孩子 6 PreOrderRec(a[x].right);//遍歷右孩子 7 }
3.4.2中序遍歷
中序遍歷,相當於遍歷左-根-右
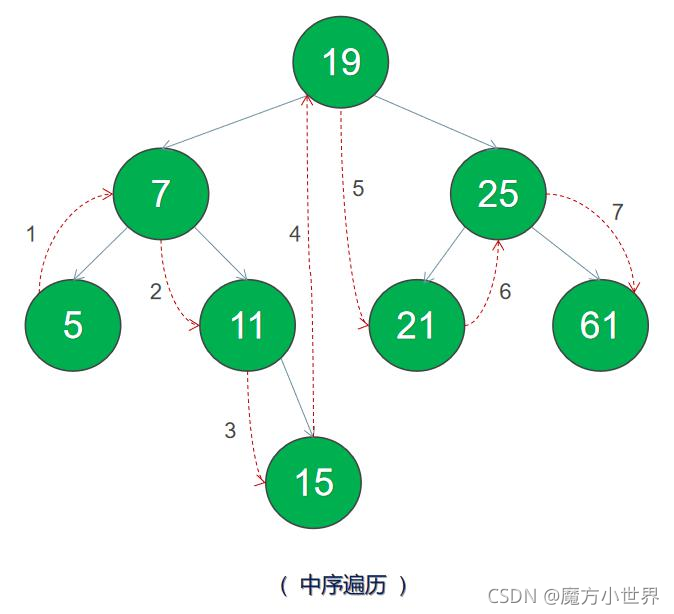
還是這個圖,但中序遍歷的結果為 5 7 11 15 19 21 25 61
1 void PreOrderRec(int x)//x為根節點 2 { 3 if (x == 0)return;//若遍歷完成,返回函數 4 PreOrderRec(a[x].left);//遍歷左孩子 5 cout<<x; 6 PreOrderRec(a[x].right);//遍歷右孩子 7 }
甚至代碼都不需要改,只需改變遍歷的順序
3.4.3後序遍歷
後序遍歷,也就是左-右-根
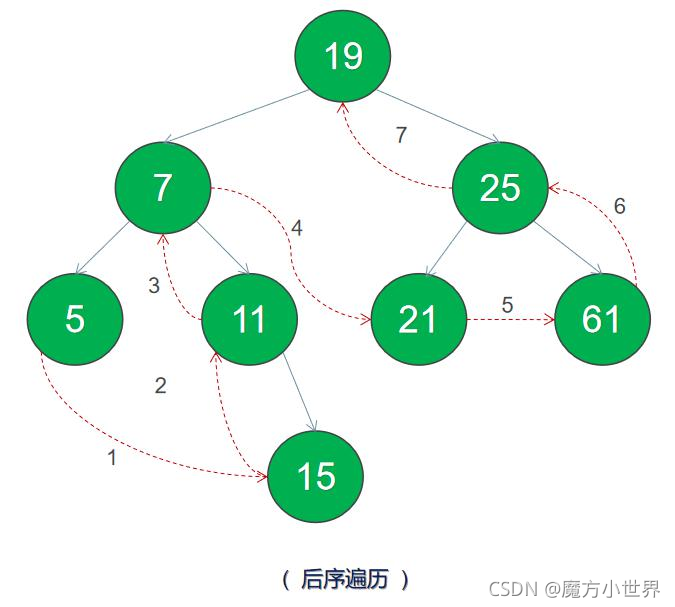
後序遍歷結果為 5 15 11 7 21 61 25 19
同樣,代碼也不需要改變
1 void PreOrderRec(int x)//x為根節點 2 { 3 if (x == 0)return;//若遍歷完成,返回函數 4 PreOrderRec(a[x].left);//遍歷左孩子 5 PreOrderRec(a[x].right);//遍歷右孩子 6 cout<<x; 7 }
以上就是二叉樹的常用操作啦,至於增加、刪除節點,就類似於鏈表的操作,由於本蒟蒻對鏈表簡直就算是白痴,此處就不再詳解了.另外,此文摘抄了
https://blog.csdn.net/qq_54169998/article/details/121108627?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522166071783716782390559337%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=166071783716782390559337&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_ecpm_v1~hot_rank-6-121108627-null-null.142^v41^pc_rank_34_1,185^v2^control&utm_term=C%2B%2B%E4%BA%8C%E5%8F%89%E6%A0%91%E8%AF%A6%E8%A7%A3&spm=1018.2226.3001.4187
一些知識點,大家有興趣可以去看看原博客


