預備知識梳理 本文中設定 block size 與 page size 大小相等。 什麼是 Block 文章的開始先解釋一下,磁碟的數據讀寫是以扇區 (sector) 為單位的,而操作系統從磁碟上讀寫數據是以塊 (block) 為單位的,一個 block 由若幹個連續的 sector 組成,使用 b ...
預備知識梳理
本文中設定 block size 與 page size 大小相等。
什麼是 Block
文章的開始先解釋一下,磁碟的數據讀寫是以扇區 (sector) 為單位的,而操作系統從磁碟上讀寫數據是以塊 (block) 為單位的,一個 block 由若幹個連續的 sector 組成,使用 block 代替 sector 能夠提升讀寫速度,相應的空間碎片會變得更大,是一種空間換時間的應用。
如何從磁碟上讀取一個位元組?
- 移動磁臂到指定的柱面。
- 移動磁頭到指定的磁軌。
- 磁碟旋轉到指定的扇區。
- 載入扇區的數據到記憶體。
- 從記憶體中讀取一個位元組。
什麼是 Page
為了更高效率的利用物理記憶體,會將其劃分為若幹個頁 (page),page 和 block 都是操作系統層面的概念,而不是硬體層面,一般來講二者的大小相等。
什麼是 Buffer
有一種特殊的 page 為 buffer page,buffer page 中存在若幹個大小相等的 buffer,每個 buffer 對應一個 block,如果 page 和 block 大小相等,那就是一個 buffer page 對應一個 block。
之所以要有 buffer,是因為記憶體和磁碟的讀寫速率相差過大,應用從磁碟上讀數據時,數據會先批量載入一部分到 buffer 中,應用再從 buffer 中讀取數據。
什麼是 5 分鐘法則
假設 1 個磁碟的價格為 30000 元,支持每秒訪問 15 次,那麼可以認為每秒訪問 1 次磁碟的成本為 2000 元,也就是每秒從磁碟上讀取 1 個 block 的成本為 2000 元,記為 2000/block/second。
假設 1 個記憶體的價格為 5000 元,大小為 4 MB,即該記憶體上約有 1000 個 page,那麼可以認為 1 個 page 的成本約為 5 元,記為 5/page。
假設有 4KB 的數據存儲在磁碟上,讀取它的頻率為 1 秒 10 次。則每秒的成本是 20000 元。如果將它記錄在記憶體中,則每秒的成本是 5 元,因此選擇將數據記錄在磁碟上是更經濟的選擇。不難算出,當讀取頻率為 1 秒 0.0025 次,即 400 秒 1 次時,成本都是 5 元,是經濟和不經濟的臨界點。那麼如何計算這個臨界點呢?
設:
- P:1MB 記憶體中有多少個 page。
- A:磁碟支持每秒訪問多少次,即每秒讀取多少個 page。
- D:磁碟驅動器價格。
- M:1MB 記憶體的成本。
- I:數據讀取頻率為多少秒 1 次。
當:
\[\frac{D/A}{I} = \frac{M}{P} \]時,為經濟和不緊急的臨界點,代入上述數據:
\[\frac{30000/15}{I} = \frac{5000/4}{1000/4} \]得出 I = 400 秒,約等於 5 分鐘,即當存儲設備價格為上述情況時,訪問頻率高於 5 分鐘 1 次的數據應該記錄在記憶體中,實際應用時,可以將從磁碟讀到的數據記錄到記憶體上,並設置 5 分鐘的生存時間,如果 5 分鐘內再次讀取該數據,則刷新生存時間,否則從記憶體中刪除。
最終我們可以得出生存時間(訪問頻率)的計算公式為:
\[I = \frac{P \times D}{A \times M} \]10 年後的 5 分鐘法則
上面的 5 分鐘法則是 Jim Gary 在 1987 年提出的,10 年後,Jim Gary 又使用了 1997 年的存儲器價格進行計算,得出 10 年後的 5 分鐘法則依然適用。
我們可以把 P/A 看作技術比率,D/M 看作經濟比率,論文中統計了 1980 - 2000 的存儲器數據,發現技術比率縮減至十分之一,經濟比率放大了十倍,可以看出,雖然存儲器一直在發展,但是 5 分鐘法則計算得出的結果依舊是穩定的。
磁碟順序訪問
上面提到的 5 分鐘法則,是只讀取 1 個 block 大小的數據,即隨機讀取數據。當順序讀取數據時,也就是讀取超過 1 個 block 的數據,由於順序讀取不需要移動磁臂磁頭、旋轉盤面,速度是遠遠大於隨機讀取的,因此順序讀取不再適用 5 分鐘法則。
如果順序讀取數據後不會再次讀取,就不需要記錄(緩存)數據到記憶體,系統只需要足夠的 buffer 讓磁碟上的數據載入到記憶體上。一般來說 buffer 的大小不會超過 1MB。
這裡的不需要記錄到記憶體是指不需要常駐記憶體以待後續訪問,而通過 buffer 載入磁碟數據到記憶體是指應用讀取數據並處理。
如果順序讀取數據後還會再次讀取,例如資料庫中的 sort、cube、rollup、join 操作都有這種行為。下麵以 sort 為例分析順序訪問操作。
兩階段排序
正常的排序是:先讀數據,再排序,再寫數據,這樣的過程稱為單階段排序。如果數據過多無法全部載入記憶體,則會採用兩階段排序,第一階段劃分所有數據為若幹個子數據集,並分別排序;第二階段歸併所有子排序結果,示意圖如下。
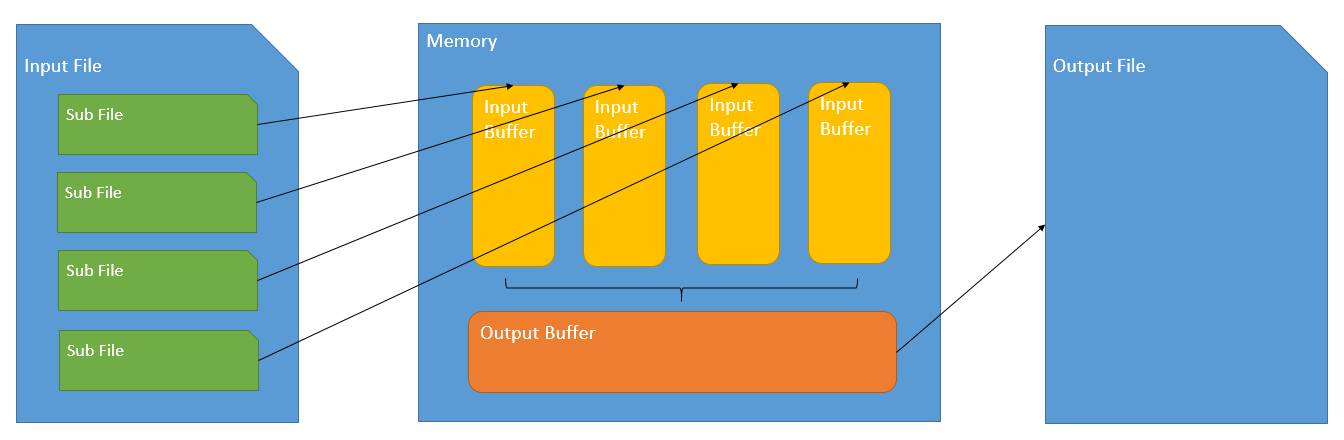
兩階段排序的記憶體需求可以由下麵的式子描述:
\[6 \times buffer\_size + \sqrt{3 \times buffer\_size \times file\_size} \]推導過程:
- 第一階段產生 file_size/memory_size 個子數據集,假設 1MB 記憶體,10MB 大小數據集,那就劃分為 10 個大小為 1MB 的子數據集,剛好可以在記憶體中排序。
- 第二階段歸併 memory_size/buffer_size 個子排序結果,一個 buffer 對應一個子數據集,假設 buffer 大小為 256KB,則一次歸併 4 個子排序結果,註意這裡的 buffer 和文章開始提的 buffer 不一樣,這裡的 buffer 是應用管理的,文章開始提的 buffer 是操作系統管理的。
在排序的設計中,file_size/memory_size 和 memory_size/buffer_size 應該是相等的。
\[\frac{file\_size}{memory\_size} = \frac{memory\_size}{buffer\_size} \]由此可以得出 memory_size 的計算公式:
\[memory\_size = \sqrt{file\_size \times buffer\_size} \]這裡的 memory_size 對應上圖中 Input Buffer 的大小,公式中更好項外面的 buffer_size 對應上圖中 Output Buffer 的大小,常數 3 和 6 取決於特定的排序演算法。
1 分鐘順序法則推導
對於相同大小的待排序數據來說,單階段排序的磁碟讀寫次數是兩階段排序的一半,但是兩階段排序相比於單階段排序只需要更小的記憶體。當記憶體大小足夠進行單階段排序時,我們是選擇單階段排序還是兩階段排序呢?
這個問題也是 5 分鐘法則公式的一個應用,1997 年的硬體規格如下:
- P:128 pages/MB
- A:64 access/second/disk
- D:2000 $/disk
- M:15 $/MB
但是由於排序是順序訪問數據,因此 P/A 技術比率不應該按照硬體參數帶入公式,已知磁碟順序訪問的平均速率在 5MB 每秒,如果 P 是 16 pages/MB,那麼 A 就是 5*16 = 80 access/second/disk(訪問一次是 1 個block 對應 1 個 page),也就是 P/A 為 0.2,帶入公式:0.2*2000/15 = 26。
計算得到 I = 26,表示 26 秒 1 次的訪問頻率為盈虧臨界值。但是排序既需要讀也需要寫,IO 成本增加一倍,盈虧臨界值應該在 52 秒,近似為 1 分鐘。
因此可以得出一分鐘順序法則:如果數據順序訪問頻率高於 1 分鐘 1 次,應當使用記憶體來緩存數據。
舉個例子,單階段排序的計算速度大概在 5GB 每分鐘,根據一分鐘順序法則,小於 5GB 的數據應當使用單階段排序。當數據大小超過了 5GB,則應該使用雙階段排序。
這裡解釋一下,這裡的 5GB 每分鐘是計算速度,對於 5GB 及以下的文件,一次性讀取全部數據到記憶體後,1 分鐘以內可以排序完成,因此訪問頻率是高於 1 分鐘 1 次;如果是 10 GB 的數據,一次性讀取數據後,需要 2 分鐘才可以排序完成,因此訪問頻率是 2 分鐘 1 次。還需要註意的是,寫回數據的問題是在 26*2 = 56 時體現的。
類似的,該法則也適用於其他順序操作,例如 group by、rollup、cube、hash join、index build 等等。
總結
對於隨機訪問的數據,訪問頻率高於 5 分鐘 1 次,就緩存在記憶體中;對於順序訪問的數據,訪問頻率高於 1 分鐘 1 次,就緩存在記憶體中。無論是隨機還是順序,前提都是數據不止訪問一次,否則不涉及緩存問題。
參考論文:The Five-Minute Rule Ten Years Later, and Other Computer Storage Rules of Thumb,論文成文於 1997 年,因此主要理解計算方法。



